
Теория_Вероятностей_КР7
.pdf
57
xk |
0 |
|
1 |
|
|
|
|
|
2 |
|
|
|
|
… |
|
k |
… |
|||||
Pn (k) |
|
−λ |
|
λ |
−λ |
|
|
|
λ2 |
|
|
|
|
|
|
|
|
|
|
λk |
… |
|
e |
|
|
1! e |
|
|
|
|
2! e−λ |
|
|
|
… |
|
k! e−k |
||||||||
Очевидно, что определение закона Пуассона корректно, т.к. основное свой- |
||||||||||||||||||||||
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ство ряда распределения∑ Pλ (k) = 1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
k =0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ |
|
∞ |
k |
е |
−λ |
|
|
∞ |
λ |
k |
|
|
|
|
|||||
Действительно, ∑ Pλ (k) = ∑ |
λ |
|
|
= |
е |
−λ ∑ |
|
|
= |
еλе− λ = 1. |
|
|||||||||||
|
|
|
|
k ! |
|
|||||||||||||||||
|
|
k =0 |
|
k =0 |
k ! |
|
|
k =0 |
|
|
|
|
||||||||||
Найдем математическое ожидание и дисперсию случайной величины X распределенной по закону Пуассона.
∞ |
|
∞ |
k |
е |
−λ |
∞ |
λ |
k −1 |
|
|
М(Х) = ∑kP (k) = ∑ |
kλ |
|
= λe−λ ∑ |
|
|
= λе−λеλ = λ . |
||||
k! |
|
(k −1)! |
||||||||
k =0 |
λ |
k =1 |
|
k =1 |
|
|||||
Для вычисления дисперсии найдем предварительно математическое ожидание квадрата случайной величины:
|
∞ |
λ |
k |
е |
− λ |
|
|
|
|
∞ |
|
λ |
k −1 |
∞ |
|
|
λ |
k −1 |
|
||||||
М ( Х2 ) = ∑k 2 |
|
|
= λе−λ∑k |
|
|
|
|
= λе− λ∑ (k −1) + |
1 |
|
|
= |
|||||||||||||
|
|
|
(k −1)! |
(k −1)! |
|||||||||||||||||||||
|
k =0 |
|
k ! |
|
|
|
k =1 |
|
k =1 |
|
|
|
|||||||||||||
∞ |
|
|
|
λ |
k −1 |
|
|
|
|
∞ |
|
λ |
k −1 |
|
|
|
|
|
|
|
|||||
= λе− λ∑(k −1) |
|
|
|
|
|
+ λе−λ ∑ |
|
|
|
|
|
= |
|
|
|
|
|
|
|||||||
(k −1)! |
(k −1)! |
|
|
|
|
|
|
||||||||||||||||||
k =2 |
|
|
|
|
k =1 |
|
|
|
|
|
|
|
|||||||||||||
∞ |
|
k −2 |
|
|
|
|
|
|
∞ |
|
k −1 |
|
|
|
|
|
|
|
|
|
|
|
|||
= λ2е−λ∑k =2 |
λ |
+ λе−λ∑k =1 |
λ |
= λ2е− λеλ + λе−λеλ = λ2 + λ. |
|
|
|
||||||||||||||||||
(k − 2)! |
(k −1)! |
|
|
|
|||||||||||||||||||||
Тогда D(X ) = M (X 2)− (MX )2 = λ 2 + λ − λ 2 = λ . |
|
|
|
|
|
|
|||||||||||||||||||
Итак, |
|
|
|
|
|
|
|
M(X)= D(X)=λ, |
|
|
|
|
(6.4) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
т.е. параметр λ пуассоновского распределения равен одновременно математическому ожиданию и дисперсии случайной величины X, имеющей это распределение.
Пример 6.2. На факультете обучается 500 студентов. Какова вероятность того, что 1 января является днем рождения одновременно для k студентов данного факультета? Вычислить эту вероятность для значений k = 0,1,2,3 .
Решение. Поскольку n = 500 является достаточно большим, а p = 1365 – достаточно малым, то можно считать, что случайная величина X распределена по закону Пуассона с параметром λ = 500365 = 1,37 .
По формуле (6.3) получаем, что P500 (0) = 1,370! 0 e−1,37 = 0,2541.
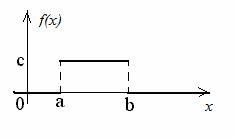
58
Для дальнейших расчетов вероятностей удобно пользоваться формулой
P (k + 1) |
= |
|
λ |
|
P (k) . |
|
||
k + 1 |
|
|||||||
n |
|
n |
|
|
|
|||
Тогда |
P |
|
(1) = |
1,37 |
P (0) = 1,37 0,2541 = 0,3481, аналогично вычисляем |
|||
|
|
|||||||
|
|
|
500 |
1 |
500 |
|||
P500 (2) = 0,2385 , P500 (3) = 0,1089 . ►
6.3. Равномерный закон распределения
Непрерывная случайная величина Х имеет равномерное распределение на отрезке [a,b], если на этом отрезке плотность распределения вероятности случайной величины постоянна, т.е.
|
c |
при |
a ≤ x ≤ b, |
(6.5) |
f (x) = |
|
при |
x < a, x > b. |
|
0 |
|
|||
На рис.14 представлен график плотности равномерно распределенной случайной величины.
Рис. 14.
+∞
Найдем значение с. По свойству 2 плотности распределения: ∫ f (x)dx = 1.
+∞ |
|
|
b |
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
|||
Получаем ∫ f (x)dx = ∫ cdx = c(b − a) = 1, |
|
|
|||||||
−∞ |
|
|
a |
|
|
|
|
|
|
следовательно, |
c = |
1 |
|
и |
|
|
|
|
|
b − a |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
при |
a ≤ x |
≤ b, |
(6.6) |
|
|
|
|
|
|||||
|
f (x) = |
− a |
|
|
|
|
|||
|
|
|
b |
|
|
> b. |
|
||
|
|
|
0 при x < a, x |
|
|||||
Так как b − a = |
1 |
, то промежуток |
[a, b], на котором имеет место равномер- |
||||||
|
|||||||||
|
c |
|
|
|
|
|
|
|
|
ное распределение, обязательно конечен. Числа a и b называют параметрами равномерного распределения.
К случайным величинам, имеющим равномерное распределение, могут относиться: время ожидания пассажирами транспорта, курсирующего с определенным интервалом; ошибка округления числа до целого (она равномерно распреде-
59
лена на отрезке [-0,5;0,5]), т.е. случайные величины, о которых известно, что все их значения лежат внутри некоторого интервала.
Определим вероятность того, что случайная величина Х примет значение, заключенное в интервале (α, β).
β |
|
β |
1 |
|
β − α . |
|
P(α < X < β ) = ∫ f (x)dx = ∫ |
dx = |
|||||
b − a |
||||||
α |
|
α |
|
b − a |
||
|
|
|
|
|||
Итак, искомая вероятность |
|
|
|
|
|
|
P(α < X < β ) = |
β − α |
, |
|
|
(6.7) |
|
|
b − a |
|
|
|
|
|
При равномерном распределении случайной величины Х вероятности попадания Х в промежутки равной длины одинаковы.
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
Найдем функцию распределения |
F(x) = ∫ f (x)dx . |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
−∞ |
|
|
|
|
|
|
|
|
Если х < a, то f(x)=0 |
и, следовательно, |
F(x) = 0 . |
|
|
|
|
|
|
|||||||
|
|
|
|
1 |
|
|
|
|
|
x |
1 |
|
x − a |
|
|
Если a ≤ x < b , то |
f (x) = |
|
|
и, следовательно, F(x) = ∫ |
dt = |
. |
|||||||||
|
b − a |
b − a |
|
||||||||||||
|
|
|
|
|
|
|
|
a |
|
b − a |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
b |
|
1 |
x |
|
|
|
|
|
Если x ≥ b , то f(x)=0 |
и, следовательно, |
F(x) = ∫ |
|
dx + ∫ 0dx = b − a = 1. |
|||||||||||
b |
− a |
||||||||||||||
|
|
|
|
|
|
|
a |
b |
|
b − a |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Таким образом, |
|
0 |
|
при |
x < a, |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||||
|
x − a |
|
|
|
|
|
|
|
|
(6.8) |
|
||||
F(x) = |
|
|
при a ≤ x < b, |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||||
|
b − a |
при x ≥ b. |
|
|
|
|
|
|
|
|
|||||
|
|
1 |
|
|
|
|
|
|
|
|
|||||
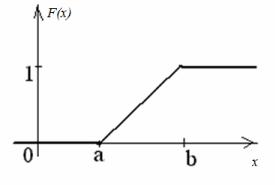
Рис.15.
На рис.15 представлен график функции распределения случайной величины, имеющей равномерное распределение.
Найдем числовые характеристики равномерного распределения.

60
По определению математического ожидания
+∞ |
b |
1 |
|
1 |
|
x |
2 |
|
b |
|
b |
2 |
− a |
2 |
= a + b . |
|
|
|
|
|
|||||||||||||
M (X ) = ∫ xf (x)dx = ∫ x |
dx = |
|
|
|
|
|
= |
|
|
|||||||
b − a |
b − a |
2 |
|
|
|
2(b − a) |
||||||||||
−∞ |
a |
|
|
|
|
a |
|
2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Для вычисления дисперсии найдем математическое ожидание квадрата равномерно распределенной случайной величины X.
+∞ |
|
|
b |
1 |
|
|
1 |
|
|
x |
3 |
|
b |
|
b |
3 |
− a |
3 |
|
= a |
2 |
+ ab + b |
2 |
|||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
M (X 2 ) = ∫ x2 f (x)dx = ∫ x2 |
dx = |
|
|
|
|
|
|
= |
|
|
|
|
|
|
. |
|||||||||||||||||
b − a |
|
b − a |
3 |
|
|
3(b − a) |
|
|
3 |
|||||||||||||||||||||||
−∞ |
|
|
a |
|
|
|
|
|
a |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Находим дисперсию равномерно распределенной случайной величины |
||||||||||||||||||||||||||||||||
|
|
|
|
D(X ) = M (X 2 ) − M 2 (X ) = |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
= |
a2 + ab + b2 |
− |
a2 + 2ab + b2 |
|
= |
a2 − 2ab + b2 |
|
= |
(b − a)2 |
. |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
3 |
|
|
|
|
4 |
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
12 |
|
|
|
|
|||||
Итак, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M (X ) = |
a + b |
|
D(X ) = |
(b − a)2 |
|
|
|
σ (X ) = |
b − a |
|
|
|
|
|
|
|
||||||||||||||||
2 |
, |
|
|
|
|
, |
|
2 3 . |
|
|
|
|
|
|
(6.9) |
|||||||||||||||||
|
12 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
Пример 6.3. Интервал движения автобуса равен 20 минутам. Найти вероятность того, что пассажир будет ожидать автобус менее 5 минут. Найти математическое ожидание и среднее квадратическое отклонение случайной величины X — времени ожидания автобуса.
Решение. Пусть случайная величина Х – время ожидания автобуса на временном отрезке [0;20]. Х имеет равномерное распределение, так как вероятность прихода, например, в пятую минуту, равна вероятности прихода в восьмую. В задаче требуется найти вероятность того, что случайная величина Х примет значение из интервала (0, 5).
Тогда по формуле (6.7) вычисляем искомую вероятность: |
|
|
||||||||
P(0 < X < 5) = |
5 |
= 0,25. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
20 |
|
|
|
|
|
|
|
|
0)2 |
|
По формулам |
(6.9) |
M (X ) = |
0 |
+ 20 |
= 10 мин, |
D(X ) = |
(20 |
− |
||
|
2 |
12 |
≈ 33 мин, |
|||||||
|
|
|
|
|
|
|
|
|||
σ (X ) = 5,74 мин. ►
6.4. Показательное распределение
Непрерывная случайная величина Х, функция плотности которой задается выражением
f (x ) = 0 при X |
< 0 |
(6.10) |
e− x при |
X ≥ 0 |
|
61
называется случайной величиной, имеющей показательное, или экспоненциальное распределение с параметром .
Величина срока службы различных устройств и времени безотказной работы отдельных элементов этих устройств при выполнении определенных условий обычно подчиняется показательному распределению. Другими словами, величина промежутка времени между появлениями двух последовательных редких событий подчиняется зачастую показательному распределению.
Найдем функцию распределения показательного закона
0 прих ≤ 0 |
|
|
|
|
F(x) = 0 |
x |
|
|
|
∫ |
f (t)dt = ∫ µ e− t dt = 1 − e− t прих > 0 |
|
||
−∞ |
0 |
|
|
|
Итак, |
0 прих ≤ 0 |
|
||
|
(6.11) |
|||
|
F(x) = |
− e− t |
. |
|
|
1 |
прих > 0 |
|
|
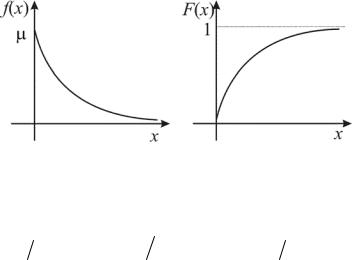
Графики дифференциальной и интегральной функций показательного распределения изображены соответственно на рис. 16.
Рис. 16.
Предлагаем самостоятельно убедиться, что для показательного распределе-
ния
M (X ) = 1 µ , D(X ) = 1 µ 2 , σ (X ) = 1 µ . |
(6.12) |
Таким образом, для показательного распределения характерно, что среднее квадратическое отклонение численно равно математическому ожиданию.
Пример 6.4. Установлено, что время ремонта телевизора случайная величина X, распределенная по показательному закону. Определить вероятность того, что на ремонт телевизора потребуется не менее 20 дней, если среднее время ремонта телевизора составляет 15 дней. Найти плотность вероятности, функцию распределения и среднее квадратическое отклонение случайной величины X.

62
Решение. По условию M (X ) = µ1 = 15 , откуда параметр = 1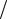 15 и по формулам
15 и по формулам
(6.10), (6.11) плотность вероятности и функция распределения имеют вид:
|
1 |
− |
1 |
x |
− |
1 |
x |
|
|
|
|
|
|
f (x) = |
|
|
e |
15 ; F(x) = 1 − e |
15 ( x ≥ 0) . |
|
|
|
|
||||
15 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Вероятность |
P( X ≥ 20) |
можно |
найти |
по |
формуле |
(5.3) |
|||||||
|
|
|
|
|
|
|
|
|
−20 |
−20 |
|
|
|
P( X ≥ 20) = F(+∞) − F(20) = 1 − (1 − e 15 ) = e |
15 = 0,264 |
. |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдем среднее квадратическое отклонение σ (X ) = M (X ) = 15 дней. ►
6.5. Нормальный закон распределения непрерывной случайной величины
Одним из наиболее часто встречающихся распределений является нормальное распределение. Оно играет большую роль в теории вероятностей и занимает среди других распределений особое положение. Нормальный закон распределения является предельным законом, к которому приближаются другие законы распределения при часто встречающихся аналогичных условиях.
Непрерывная случайная величина Х имеет нормальное распределение (распределена по нормальному закону), если плотность распределения вероятности f(x) имеет вид
f (x) = |
|
1 |
− (x−a)2 |
(6.13) |
σ |
е 2σ 2 . |
|||
|
2π |
|
|
где a и σ – некоторые постоянные, называемые параметрами нормального распределения.
Тогда функция распределения F(x) принимает вид
F(x) = |
|
1 |
x |
− |
(t − a)2 |
|
(6.14) |
|
∫ е |
2σ 2 dt . |
|||||
|
σ |
2π |
−∞ |
|
|
|
|
Как видно из формул (6.13) и (6.14), нормальное распределение определяется двумя параметрами: a и σ.
Параметры а и σ нормального распределения имеют простую геометрическую интерпретацию, для выяснения которой исследуем поведение функции f(x). В дальнейшем кривую нормального распределения (график функции f(x)) будем называть нормальной кривой.
График плотности нормального распределения f(x) представлен на рис. 17.

63
Рис. 17.
Нормальная кривая имеет колоколообразную форму. Эта форма является отличительной чертой нормального распределения. Иногда нормальную кривую называют кривой Гаусса.
Перечислим основные свойства графика функции f(x).
1.Областью определения функции f(x) является вся числовая ось.
2.Функция f(x) может принимать только положительные значения, т.е. f(x)>0.
3.Предел функции f(x) при неограниченном возрастании x равен нулю, т.е. ось ОХ является горизонтальной асимптотой графика функции.
4.Функция f(x) имеет в точке х=а максимум, равный 1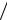 (σ
(σ  2π ).
2π ).
5.График функции f(x) симметричен относительно прямой х=а.
6.Нормальная кривая в точках x = a ± σ имеет перегиб.
Определим основные числовые характеристики нормального распределе-
ния.
Найдем математическое ожидание нормально распределенной случайной величины.
∞ |
|
∞ |
(x−a)2 |
|
|
||
M (X ) = ∫ xf (x)dx = |
1 |
∫е− |
2σ 2 xdx . |
|
|||
−∞ |
σ 2π −∞ |
|
|
x − a |
|
||
Введем новую переменную u по формуле u = |
. Тогда x=σu+a, a dx=σdu, |
||||||
σ |
|||||||
|
|
|
|
|
|
||
причем пределы интегрирования остаются теми же, в чем нетрудно убедиться. Итак, получаем
|
1 |
∞ |
(σu + a)е−u2 2du = |
σ |
∞ |
a |
∞ |
M (X ) = |
∫ |
∫uе−u2 2du + |
∫ е−u2 2du . |
||||
|
2π |
−∞ |
2π |
−∞ |
2π |
−∞ |
|
Первый из интегралов в правой части полученного равенства равен нулю как интеграл от нечетной функции в симметричных пределах, а второй интеграл (так называемый интеграл Пуассона)

64
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ е−u2 |
2du = |
|
|
2π . |
|
|
(6.15) |
||||||||
|
|
|
|
a |
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда M (X ) = |
|
|
2π = a . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2π |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Таким образом, параметр |
а нормального распределения равен математиче- |
|||||||||||||||||||||
скому ожиданию соответствующей случайной величины, т.е. |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
M(X)=a. |
|
|
|
|
|
|
|
|
(6.16) |
||||
При вычислении дисперсии имеем |
|
|
|
|
|
|
|
|
|
|||||||||||||
D(X ) = ∞∫ (x − M (X ))2 f (x)dx = |
|
|
1 |
|
|
∞∫(x − a)2 e− |
(x−a)2 |
|
||||||||||||||
|
|
|
|
2σ 2 |
dx . |
|||||||||||||||||
|
−∞ |
|
|
|
|
|
|
|
|
|
σ |
|
|
2π −∞ |
|
|
|
|||||
Введем переменную u по формуле |
u = |
x − a |
. В результате получаем |
|||||||||||||||||||
|
||||||||||||||||||||||
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
σ |
|
∞ |
|
|
|
|
D(X ) = |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
σ |
2 |
|
|
|
|
|||
|
|
∫ σ 2u2е−u2 2σdu = |
|
|
|
∫u2е−u2 2du . |
|
|||||||||||||||
|
σ |
2π |
−∞ |
|
|
|
|
|
|
|
|
|
|
|
2π |
|
−∞ |
uе−u2 2du = dv , откуда dt=du, |
||||
Далее интегрируем |
по частям, полагая u=t, а |
|||||||||||||||||||||
v = −е−u2 2 . Тогда |
|
|
|
|
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|||
|
σ 2 |
|
−u |
2 |
2 |
|
∞ |
|
−u |
2 |
|
2 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
D(X ) = |
|
|
|
|
|
|
|
+ ∫ |
е |
|
|
du |
|
|
|
|
||||||
|
2π |
− uе |
|
|
|
|
|
|
|
|
|
. |
|
|
|
|||||||
|
|
|
|
|
|
|
|
−∞ |
−∞ |
|
|
|
|
|
|
|
lim u |
еu2 / 2 = 0 ( по правилу |
||||
Первое из слагаемых в скобках равно нулю, так как |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u→±∞ |
|
|
Лопиталя), а второе равно |
|
2π . Следовательно D(X ) = |
σ 2 |
2π = σ 2 . |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2π |
|
Итак, дисперсия нормально распределенной случайной величины Х равна |
||||||||||||||||||||||
σ 2 , т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
DX = σ 2 , |
|
|
|
|
|
|
|
(6.17) |
|||||
а σ не что иное, как среднее квадратическое отклонение, поскольку
σ ( X ) = D( X ) =  σ 2 = σ .
σ 2 = σ .
После вычисления математического ожидания и дисперсии становится ясным вероятностный смысл параметров а и σ нормального распределения.
В дальнейшем дисперсию случайной величины, распределенной нормально, будем обозначать σ 2 , а математическое ожидание – а.
Определим функцию распределения случайной величины Х, имеющей нормальное распределение.
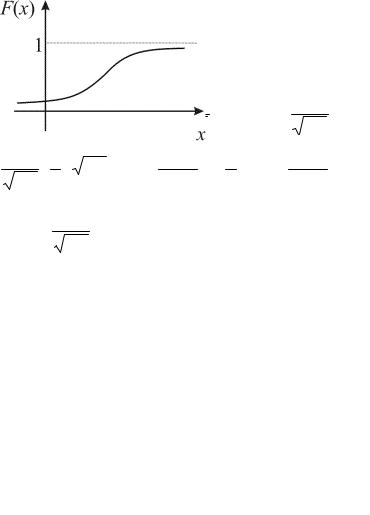
x |
x |
1 |
e− |
(u−a)2 |
|
F(x) = ∫ |
f (u)du = ∫ |
|
|
||
|
2σ2 |
||||
|
|
||||
−∞ |
−∞ σ |
2π |
|
|
|
Обозначив u σ− a = t, получим
65
du .
|
|
|
|
|
x−a |
|
|
t 2 |
|
|
0 |
|
|
t 2 |
|
|
x−a |
|
t 2 |
||||||
|
|
|
1 |
|
σ |
|
|
1 |
|
|
|
1 |
|
σ |
|||||||||||
F(x) = |
|
|
∫ |
e− |
|
|
dt = |
|
∫e− |
|
|
dt + |
|
∫ e− |
|
dt = |
|||||||||
|
|
2 |
|
2 |
|
2 |
|||||||||||||||||||
|
|
|
2π |
|
−∞ |
|
|
|
|
|
2π |
−∞ |
|
|
|
|
2π |
0 |
|
|
|
||||
= |
1 |
|
1 |
|
2π |
|
|
|
|
x − a |
= |
1 |
|
|
|
x − a |
|
|
|||||||
2π |
2 |
+ Φ0 |
|
2 |
+ Φ 0 |
σ |
. |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
σ |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
1 |
|
x |
|
t 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Φ0 (x) = |
|
|
∫e− |
|
|
||||||||||||||||||||
|
|
2 |
dt — нормированная функция Лапласа (см. пункт 3.3). |
||||||||||||||||||||||
|
|
|
|
2π |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Итак, функция распределения случайной величины Х имеет вид |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
F(x) = |
1 |
+ Φ 0 |
x − a |
|
|
|
(6.18) |
||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
. |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σ |
|
|
|
|
|
|
|||
График функции распределения представлен на рис.18.
.
Рис.18.
Вероятность попадания случайной величины Х, имеющей нормальное распределение, в заданный интервал
Используя функцию распределения случайной величины Х, найдем вероятность попадания ее значений в интервал (α, β).
P(α < X < β ) = F(β ) − F(α ) = 1 |
+ Φ0 β − a |
|
− 1 |
+ Φ0 |
|
x − a |
|
= |
||||||
|
||||||||||||||
|
|
|
|
2 |
|
σ |
2 |
|
σ |
|
|
|||
= Φ0 β − a |
− Φ 0 |
α − a |
. |
|
|
|
|
|
|
|
|
|
|
|
σ |
|
σ |
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, |
|
|
β |
− a |
α |
− a |
|
|
|
|
|
|||
P(α < X < β ) = Φ0 |
|
|
|
|
(6.19) |
|||||||||
|
σ |
|
− Φ0 |
|
. |
|
|
|
|
|||||
|
|
|
|
|
|
σ |
|
|
|
|
|
|
||
Пример 6.5. Найти вероятность попадания в интервал (−2; 3) |
для нормально рас- |
|||||||||||||
пределенной случайной величины с параметрами |
a = 2, |
σ = 3. |
|
|
||||||||||

66 |
|
|
|
|
|
|
|
|
Решение. По формуле (6.19) имеем P(−2 < X < 3) = Φ 0 |
|
3 − 2 |
− Φ 0 |
− 2 − 2 |
|
= |
||
|
|
3 |
|
|
|
3 |
|
|
= Φ0 (0,33) − Φ0 (−1,33) = 0,1293 + 0,4082 = 0,5375. Значения |
функции |
Φ 0 (x) вы- |
||||||
числяли по таблице (см. Приложение 2)► |
|
|
|
|
|
|
|
|
Найдем вероятность того, что случайная величина Х, распределенная нормально с параметрами а и σ , отклонится от своего математического ожидания на величину, меньшую ε. Другими словами, найдем вероятность выполнения неравенства X − a < ε . Эта вероятность равна вероятности выполнения равносильно-
го двойного неравенства a − ε < X < a + ε . Воспользовавшись равенством (6.19),
имеем и учитывая нечетность Φ0 (x) , получаем |
|
|
|
|
|
|||||||||||||
P( |
|
X − a |
|
< ε )= P(a − ε < X |
< a + ε ) = Ф0 |
a + ε |
− a |
− Ф0 |
a − ε |
− a |
= |
|||||||
|
|
|||||||||||||||||
|
|
|
σ |
|
|
σ |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||
|
|
ε |
|
− ε |
|
ε |
|
|||||||||||
|
|
|
|
|
||||||||||||||
= Ф0 |
|
|
− Ф0 |
|
= 2Ф |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
σ |
|
σ |
|
σ |
|
|
|
|
|
|
|
|
||||
Таким образом, |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
P( |
|
|
X − a |
|
|
|
< ε )= 2Ф0 (ε σ ). |
(6.20) |
||||||||
|
|
|||||||||||||||||||||||||||
Для стандартной случайной величины Х, когда а=0, σ=1, последнее равенст- |
||||||||||||||||||||||||||||
во принимает вид |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P( |
|
X |
|
< ε )= 2Ф0 (ε ). |
(6.21) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Обозначим ε σ = u . Тогда из равенства (6.20) следует, что |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
P( |
|
X − a |
|
< σ u)= Ф0 (u). |
(6.22) |
|||||||||||
|
|
|||||||||||||||||||||||||||
Из равенства (6.22) при различных значениях u |
получаем различные значе- |
|||||||||||||||||||||||||||
ния вероятности P( |
|
X − a |
|
< ε ): |
|
|
||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||
P( |
|
|
X − a |
|
|
|
|
|
< σ )= 2Ф0 (1) = 0,6837 |
при u=1, |
|
|||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||
P( |
|
|
X − a |
|
|
< 2σ )= 2Ф0 (2) = 0,9545 |
при u=2, |
|
||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
P( |
|
X − a |
|
< 3σ )= 2Ф0 (3) = 0,9973 |
при u=3. |
|
||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
Последнее из равенств показывает, что вероятность отклонения случайной величины Х, распределенной нормально, от своего математического ожидания а меньше чем на 3σ, близка к 1, т.е. такое отклонение является практически достоверным событием. Другими словами, вероятность того, что то или иное значение величины Х не попадает в интервал с границами а ± 3σ , равна 0,0027, т.е. близка к нулю. Такое событие можно считать практически невозможным.
Сформулируем теперь правило «трех сигм».
