Теория_Вероятностей_КР7

17

События A, B, C, D являются попарно несовместными.

Тогда искомые вероятности найдем с помощью формул (2.4), (2.5):

а) P(A + B) = P(A) + P(B) = 7020 + 1570 = 12 .

б) P( A + B + C) = P(A) + P(B) + P(C) = 1070 + 1570 + 7020 = 149 .

Для вычисления вероятности суммы трех событий можно воспользоваться свойством вероятности С5 (событие А+В+С и событие D являются противопо-

ложными): P(A + B + C) = 1− P(D) = 1− 7025 = 149 . ►

Пример 2.17. На стеллаже в библиотеке стоит 15 учебников, причем 5 из них в переплете. Библиотекарь берет три учебника. Найти вероятность того, что хотя бы один из взятых учебников окажется в переплете.

Решение. Рассмотрим два способа решения задачи. Первый способ. Обозначим следующие события:

А – «хотя бы один учебник в переплете»; В – «один из взятых учебников в переплете, два – без переплета»; С – «два в переплете, один без переплета»;

D – «все три учебника в переплете».

Очевидно, что А=В+С+D (события В, С, D – несовместные). Найдем вероятности событий В, С, и D.

Второй способ. Обозначим следующие события: А – «хотя бы один учебник в переплете»;

A – «ни один из взятых учебников не имеет переплета».

Так как события А и A противоположные, то

Пример 2.18. Среди одинаковых 11 изделий находятся 3 бракованных. Произвольно вынимают три изделия. Найти вероятность того, что среди них хотя бы одно бракованное.

Решение. События «среди вынутых трех изделий хотя бы одно бракованное» и «среди вынутых трех изделий нет бракованных» являются противоположными.

18

Обозначим их А и А соответственно. Найдем вероятность события А. Число всех исходов испытания равно n = C113 , а число исходов, благоприятствующих событию А равно m = C83 .

Пример 2.19. Вероятность того, что сотрудник знает немецкий язык, равна 0,3, французский — 0,2 и знает оба языка 0,02. Какова вероятность, что наудачу вы-

бранный сотрудник знает немецкий или французский язык? Какова вероятность,

что наудачу выбранный сотрудник не знает ни немецкого, ни французского языка?

Решение. Обозначим следующие события:

A — «наудачу выбранный сотрудник знает немецкий язык»; В — «наудачу выбранный сотрудник знает французский язык»; А В — «наудачу выбранный сотрудник знает оба языка»;

С — «наудачу выбранный сотрудник знает немецкий или французский язык»;

D — «наудачу выбранный сотрудник не знает ни немецкого, ни французского языка».

События А и В совместные.

По условию задачи: P(A) = 0,3; P(B) = 0,2; P(AB) = 0,02 .

Очевидно, что С=А+В.

Тогда P(C) = P(A + B) = P(A) + P(B)-P(AB) = 0,3 + 0,2 − 0,02 = 0,48.

Найдем вероятность наступления события D. События C и D являются противоположными, учитывая законы де Моргана, получим: D = A B = A + B = C .

Т.о. P(D) = 1− P(C) = 1− 0,48 = 0,52 . ►

2.5. Условная вероятность события. Теорема умножения вероятностей. Независимые события

На практике часто встречаются ситуации, когда наступление некоторого события значительно меняет возможности наступления других событий и их вероятности. Если произошло событие В, то новая вероятность события А называется условной вероятностью и обозначается Р(А/В), говорят: «вероятность события А

при условии В».

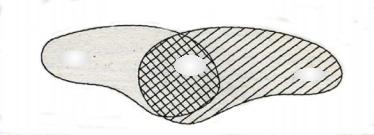
Мы знаем, что наступило событие B, но каким из элементарных событий закончился эксперимент неизвестно. Поэтому В оказывается достоверным событием и играет роль пространства элементарных событий Ω (рис. 8). Тогда любое

19

подмножество множества B является случайным событием в новых условиях, в

том числе A B .

Рис. 8.

Пример 2.20. Опыт: бросание игральной кости. Известно, что выпало более трех очков. Какова при этом вероятность того, что выпало четное число очков?

Решение. Пространство элементарных исходов при одном подбрасывании кубика состоит из шести точек: Ω = {ω1,ω2 ,ω3 ,ω4 ,ω5 ,ω6 } (событие ωi означает, что

в результате бросания кости выпало i очков, i = 1,2,3,4,5,6).

Слова «известно, что выпало более трех очков» означают, что в эксперименте произошло событие В = {ω4 ,ω5 ,ω6}.

Вопрос «какова при этом вероятность того, что выпало четное число оч-

ков?» означает, что нас интересует, в какой доле случаев при осуществлении B

происходит и А. Тогда, A B = {ω4 ,ω6 }.

Используем классическое определение вероятности. Событию А B благоприятствует 2 элементарных исхода из ПЭС В, поэтому P(A/В) = 2/3. ►

Равенство (2.9) называют теоремой или правилом умножения вероятно-

стей. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, найденную в предположении, что первое событие произошло.

Это правило обобщается на случай n событий:

20

P(A1 A2 ... An ) = P(A1 ) P(A2 /A1 ) P(A3 /A1 A2 ) ... P(An /A1 A2 ... An-1 ). (2.10)

Так для трех событий А1, А2 , А3 получаем

P(A1 A2 A3 ) = P(A1 ) P(A2 /A1 ) P(A3 /A1 A2 ) .

Пример 2.21. В урне находится 4 белых, 3 синих и 2 черных шара. Наудачу последовательно вынимают 3 шара. Какова вероятность того, что 1-й шар будет бе-

лым, 2-й — синим, 3 — черным (событие А)?

Решение. Обозначим следующие события: А1 — «первым вытащили белый шар»;

А2 — «вторым — синий»;

А3 — «третьим — черный».

Тогда событие А представится в виде А = A1 A2 A3 . По правилу умножения

Пример 2.22. К экзамену надо подготовить 25 вопросов. Студент пришел на экзамен, зная 20. Какова вероятность того, что студент ответит на все три вопроса

билета?

Решение. Обозначим следующие события:

А1 — «студент знает первый вопрос»;

А2 — «студент знает второй вопрос»;

А3 — «студент знает третий вопрос»;

A — «студент ответит на все три вопроса билета».

Тогда событие А представится в виде А= A1 A2 A3 . По правилу умножения

P(А2 / А1) = 1924 , т.к. вопросов осталось 24, а число вопросов, на которые студент

знает ответ, уменьшилось на 1, P(А3 / А1 А2 ) = 1823 , т.к. студент правильно ответил уже на два вопроса.

21

Следовательно, P(A1 A2 A3 ) = 2025 1924 1823 = 11557 ≈ 0,5 . ►

Пример 2.23. 21% работников некоторой фирмы получают высокую зарплату.

Среди них отношение числа мужчин и женщин равно 14,6:6,4. известно также, что 40% работников фирмы составляют женщины. Необходимо выяснить, суще-

ствует ли на фирме дискриминация женщин в оплате труда.

Решение. Обозначим следующие события:

А — «случайно выбранный работник получает высокую зарплату»; В — «случайно выбранный работник – женщина».

По условию задачи дано, что P(A) = 0,21 , P(В) = 0,4 , P(А В) = 0,064 .

Найдем условную вероятность (вероятность получения работником высокой зарплаты, при условии, что этот работник — женщина)

Т.к. P(A/B) < P(A), то труд женщин является менее оплачиваемым. ►

Правило умножения вероятностей имеет особо простой вид, если события, образующие произведения независимы. Событие А называется независимым от события В, если осуществление события В не изменяет вероятности события А, т.е. условная вероятность события А равна его безусловной вероятности:

Из равенства (2.9), с учетом равенства (2.11) нетрудно доказать следующую

лемму.

Лемма о взаимной независимости событий. Если событие А не зависит от со-

бытия В, то и событие В не зависит от события А.

Для независимых событий правило умножения вероятностей (2.10) прини-

мает вид:

т.е. вероятность произведения двух независимых событий равна произведению вероятностей этих событий.

Нетрудно доказать обратное утверждение: если для двух событий выполня-

ется равенство (2.12), то эти события независимые.

Можно показать, что если события А и В независимы, то независимы собы-

тия А и В, А и В , А и В .

Понятие независимости может быть распространено на случай n событий.

События A1, A2 , ..., An называются независимыми (или независимыми в совокуп-

22

ности), если каждое из них не зависит от произведения любого числа остальных

событий и от каждого в отдельности.

имная независимость событий A1 , A2 ,..., An .

Пример 2.24. Подбрасываются две игральные кости. Очевидно, Ω = {(i, j) |1 ≤ i, j ≤ 6}, | Ω |= 36 .

C= {(i, j) | i + j = 9}

ивычислим их вероятности и вероятности их пересечений.

P( A) = P(B) = 1836 = 12 , P(C) = 364 = 19 ,

P( A B) = 366 = 16 ≠ 14 = P( A) P(B) ,

P(A C) = 361 ≠ 181 = P(A) P(C) ,

P(B C) = 363 = 121 ≠ 181 = P(B) P(C) ,

т.е. А, В и С попарно зависимы,

но P(A B C) = 361 = P(A) P(B) P(C) . ►

Пример 2.25. В первом ящике 2 белых и 10 черных шаров, во втором 8 белых и 4

черных шара. Из каждого ящика вынули по шару. Найти вероятность того, что один из вынутых шаров белый, а другой – черный.

Решение. Обозначим следующие события:

А – «вынули белый шар из первого ящика»: P(A) = 16 ;

A– «вынули черный шар из первого ящика»: P(A) = 56 ;

В– «белый шар из второго ящика»: P(B) = 23 ;

B– «черный шар из второго ящика»: P(B) = 13 ;

С– «один из вынутых шаров белый, а другой – черный».

23

Очевидно, что С= A B + A B . Т.к. А и B события независимые, то по тео-

Пример 2.26. Вероятность попадания в цель у первого стрелка 0,8, у второго – 0,9. Стрелки делают по выстрелу. Найти вероятность: а) двойного попадания; б) хотя бы одного попадания, в) одного попадания.

Решение. Обозначим следующие события:

А – «попадание первого стрелка»: Р(А)=0,8;

В – «попадание второго стрелка»: Р(В)=0,9. Тогда A – «промах первого»: P(A) = 1 − 0,8 = 0,2 ;

B – «промах второго»: P(B) = 1 − 0,9 = 0,1.

Найдем нужные вероятности.

а) А В – событие, соответствующее тому, что произошло двойное попадание

(A и B независимые): Р(А В)=Р(А) Р(В)=0,72.

б) A B – «двойной промах» ( A и B независимые):

P(A B) = P(A) P(B) = 0,02 .

в) А+В – событие, соответствующее тому, что произошло хотя бы одно попадание (A и B совместные):

P(A + B) = P(A) + P(B) − P(AB) = 0,8 + 0,9 − 0,72 = 0,98 .

г) A B + A B — событие, соответствующее тому, что произошло одно по-

падание: P(A B + A B) = P(A B) + P(A B) = 0,8 0,1 + 0,2 0,9 = 0,26 . ►

Пример 2.27. Студент разыскивает нужную ему формулу в трех справочниках.

Вероятности того, что формула содержится в первом, втором и третьем справочниках равны 0,6, 0,7 и 0,8 соответственно. Найти вероятности того, что формула

содержится а) только в одном справочнике; б) только в двух справочниках; в) во

всех трех справочниках.

Решение. Обозначим следующие события:

А – «формула содержится в первом справочнике»;

В– «формула содержится во втором справочнике»;

С– «формула содержится в третьем справочнике». Воспользуемся теоремами сложения и умножения вероятностей.

24

а) A B C + A B C + A B C — событие, соответствующее тому, что формула содержится только в одном справочнике (в сумму входят несовместные события, и каждое из них является произведением независимых событий):

P(A B C + A B C + A B C) = P(A B C) + P(A B C) + P(A B C) =

=0,6·0,3·0,2+0,4·0,7·0,2+0,4·0,3·0,8 = 0,188.

б) A B C + A B C + A B C — событие, соответствующее тому, что формула содержится только в двух справочниках (в сумму входят несовместные события, и каждое из них является произведением независимых событий):

P(A B C + A B C + A B C) = 0,6 0,7 0,2 + 0,6 0,3 0,8 + 0,4 0,7 0,8 = 0,452 .

в) А В С — событие, соответствующее тому, что формула содержится во всех трех справочниках (произведение независимых событий):

P(А В С)=0,6·0,7·0,8=0,336. ►

Пример 2.28. Из 10 деталей 7 – стандартные. Наудачу берут 6 деталей. Найти вероятность того, что среди них: а) не более одной нестандартной; б) не более двух нестандартных.

Решение.

а) Обозначим события:

А – «среди взятых 6 деталей нестандартных нет»; В – «в 6 выбранных деталях одна нестандартная».

Тогда А+В – событие, соответствующее тому, что среди 6 деталей не более

б) Пусть теперь событие А – «в шести взятых деталях не более двух нестан-

дартных». Тогда A – «в выбранных деталях более двух нестандартных», т.е. три.

25

2.6. Формула полной вероятности

Пусть события H1, H2 ,K, Hn образуют полную группу событий и A —

Пример 2.29. В трех одинаковых урнах лежат шары: в первой — 5 белых и 3 черных, во второй — 2 белых и 6 черных, в третьей — 3 белых и 1 черный. Из случайно выбранной урны вынут шар. Найти вероятность того, что он белый.

Решение. Будем считать гипотезами выбор одной из урн: Hi — «выбрана i-я урна» (i = 1,2,3) . Поскольку урны одинаковы, каждую из них можно выбрать с

одинаковой вероятностью, а так как сумма вероятностей гипотез равна 1, то вероятность каждой гипотезы P(H1) = P(H2 ) = P(H3 ) = 1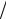3.

Условная вероятность события A , т. е. извлечения белого шара из урны,

определяется по классическому определению вероятности (количеством благоприятных исходов при этом является число белых шаров, а числом возможных

исходов — общее число шаров в урне).

Поэтому P(A / H1) = 5 8, P(A / H2 ) = 2 8 = 1 4, P(A / H3 ) = 3 4.

Пример 2.30. В группе из 10 студентов, пришедших сдавать экзамен, 3 студента подготовлены отлично (знают 20 вопросов из 20), 4 — хорошо (знают 16 вопросов из 20), 2 — посредственно (знают 10 вопросов) и 1 — плохо (знает 5 вопро-

сов). Какова вероятность, что наугад вызванный студент ответит на 3 произвольно заданных вопроса.

Решение. Введем гипотезы:

H1 — «студент подготовлен отлично»,

H2 — «студент подготовлен хорошо»,

H3 — «студент подготовлен посредственно»,

H4 — «студент подготовлен плохо».

26

Найдем вероятности гипотез. P(H1) = 0,3, P(H2 ) = 0,4 , P(H3 ) = 0,2 ,

P(H4 ) = 0,1. Действительно, P(H1) + P(H2 ) + P(H3 ) + P(H4 ) = 1.

Пусть событие A — «студент ответил на три вопроса». Найдем условные вероятности события A. Очевидно, P(A/ H1) = 1,

Тогда по формуле полной вероятности

P(A) = 0,3 1 + 0,4 0,491 + 0,2 0,105 + 0,1 0,009 = 0,5183 . ►

Пример 2.31. По цели произведено три последовательных выстрела. Вероятность попадания при первом выстреле р1=0,3, при втором р2=0,6, при третьем р3=0,8. При одном попадании вероятность поражения цели r1=0,4, при двух попаданиях r2=0,7, при трех попаданиях r3=1. Определить вероятность поражения цели при трех выстрелах.

Решение. Обозначим следующие гипотезы:

Н1 – «было одно попадание»; Н2 – «было два попадания»; Н3 – «было три попадания»;

Н4 – «не было ни одного попадания».

Определим вероятности гипотез. По теоремам умножения и сложения вероятностей будем иметь

P(Н1) = p1(1− p2 )(1− p3 ) + (1− p1) p2 (1− p3 ) + (1− p1)(1− p2 ) p3 = 0,332, P(Н2 ) = p1 p2 (1− p3 ) + p1(1− p2 ) p3 + (1− p1) p2 p3 = 0,468,

P(Н3 ) = p1 p2 p3 = 0,144 .

P(Н4 ) = (1 − p1)(1 − p2 )(1 − p3 ) = 0,056 .

Действительно,

P(H1) + P(H2 ) + P(H3 ) + P(H4 ) = 0,332 + 0,468 + 0,144 + 0,056 = 1.

Пусть событие А – «цель поражена». Найдем условные вероятности поражения цели при осуществлении каждой из гипотез.

P(A/ Н1) = 0,4, P(A / Н2 ) = 0,7 , P(A / Н3 ) = 1, P(A/ Н4 ) = 0 .