
Теория_Вероятностей_КР7
.pdf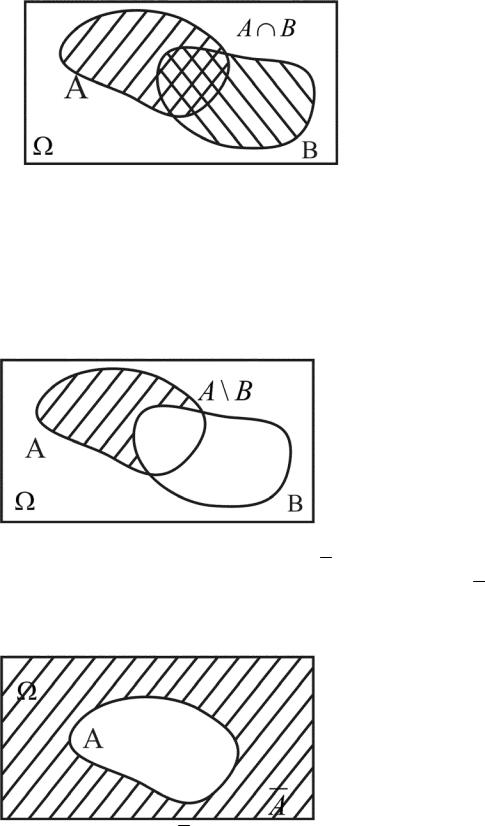
7
Произведением событий А и В называется событие, состоящее в совместном наступлении этих событий.
Произведение двух событий A Ω и B Ω (обозначается А·В или A ∩ B ) соответствует множеству, которое содержит элементы, общие для событий А и В, т.е. пересечению множеств А и В (см. рис.2).
Рис. 2. A B
События А и В называются несовместными, если их произведение есть невозможное событие, т. е. A B = { }.
Разностью событий А и В называется событие, происходящее тогда и только тогда, когда происходит событие А, но не происходит событие В.
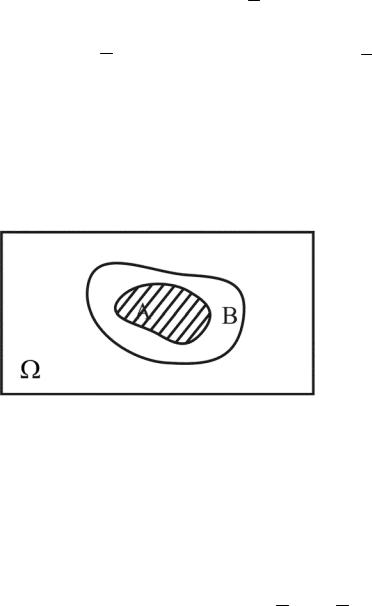
Разность событий A Ω и B Ω (обозначается А-В или A\ B ) соответствует множеству, которое содержит элементы события А, не принадлежащие событию В
(см. рис.3).
Рис.3. А\В
Противоположным событию А называется событие A , которое происхо-
дит тогда и только тогда, когда не происходит событие А (т. е. наступление A означает, что событие А не наступило).
Рис.4. A
8
Противоположное событию A Ω событие A Ω является дополнением множества А (см. рис.4).
Очевидно, что события А и A являются несовместными: A А = .
Событие А влечет событие В (или А является частным случаем В), если из того, что происходит событие А, следует, что происходит событие В. Множе-
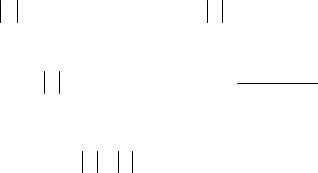
ственная трактовка данного факта проиллюстрирована на рис. 5. Событие А влечет событие В (обозначается A B ), если каждый элемент события А содержится в В.
По определению: A для любого А.
Рис. 5. A B
Если A B и B A , то события А и В называются равными; записывают
А = В. |
|
|
События A1, A2 ,..., An |
образуют полную группу, если они попарно несовме- |
|
стны и в результате каждого опыта происходит одно и только одно из них. |
||
|
A1 + A2 + ... + An = Ω |
(2.0) |
|
|
i ≠ j |
Ai Aj = , i, j = 1,2,..., n, |
||
Полную группу образуют, например события А и А ( A + А = Ω ).
Пример 2.4. Вернемся к опыту описанному в примере 2.1. Определим следующие события.
Событие А — «выпадение нечетного числа очков»: A = {ω1,ω3 ,ω5}, событие В — «выпадение четного числа очков»: B = {ω2 ,ω4 ,ω6 }, событие С — «выпадение 3 очков»: C = {ω3},
событие D — «выпадение менее 3-х очков»: D = {ω1,ω2 }, событие Е — «выпадение не менее 3-х очков»: E = {ω3 ,ω4 ,ω5 ,ω6 }.
Суммой событий A и B является ПЭС: A + B = {ω1,ω2 ,ω3 ,ω4 ,ω5 ,ω6 }= Ω .
Суммой событий C и D является событие, означающая выпадение не более трех очков: C + D = {ω1,ω2 ,ω3}.
Произведением событий А и В является невозможным событием: A B = { }.

9
Произведением событий В и E является событие, означающее выпадение 4-х очков или 6-ти очков. : B E = {ω4 ,ω6 }.
Противоположным к событию А является событие В: A = B .
Очевидно, что событие С влечет событие А: С A. События А и В образуют полную группу. ►
Отметим некоторые очевидные следствия приведенных выше определений:
|
A + = A, A + Ω = Ω , A + A = A, A + B = B + A , |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
A = , A Ω = A , A A = A , A B = B A |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
A + |
|
= Ω , A |
|
= , A \ B = A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
A |
A |
B |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
= , |
|
= Ω , A = B |
|
= |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
Ω |
|
A |
B |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Часто оказываются полезными теоретико-множественные |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
законы де Моргана: |
|
|
|
законы дистрибутивности: |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
, |
|
|
|
|
|
|
(A + B) C = A C + B C , |
|||||||||||||||
|
|
|
|
|
|
|
|
A + B |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
A |
B |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
= |
|
+ |
|
, |
|
|
|
|
|
|
A B + C = (A + С) (B + C) . |
|||||||||||||||||
|
|
|
|
|
|
|
|
A B |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
A |
B |
|||||||||||||||||||||||||||||
Докажем, например, тождество |
|
= |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
A + B |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
A |
B |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω A |
|
ω |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Пусть ω A + B ω A + B |
|
|
|
|
ω A B , что и |
|||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ω B |
|
ω B |
|
|
|
|
|
||||||
требовалось доказать.
Т.о. мы построили систему случайных событий F, которая вместе с любыми двумя событиями содержит их сумму, произведение, разность. Такая система F
называется алгеброй случайных событий.
Приведем примеры алгебры событий.
1.F = {Ω, } — система, состоящая из Ω и пустого множества.
2.F = {A, A,Ω, } — система, порожденная событием A.
3.F = {A : A Ω} — совокупность всех (включая и пустое множество ) подмножеств Ω.
Пример 2.5. Рассмотрим опыт, описанный в примере 2.1. Алгебра событий F для
множества Ω состоит из 26 = 64 подмножеств этого множества, которые содержат по одному, два, три, четыре, пять, шесть элементарных событий и пустое множество:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F = |
, {ω |
}, {ω |
2 |
},..., {ω |
6 |
}, {ω |
,ω |
2 |
}, {ω |
,ω |
}, ..., {ω |
5 |
,ω |
6 |
},{ω |
,ω |
2 |
,ω |
},..., {ω |
,ω |
2 |
,ω |
,ω |
4 |
},..., Ω |
.► |
|
|
|
1 |
|
|
1 |
|
1 |
3 |
|
|
1 |
|
3 |
1 |
|
3 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10
2.3. Определение вероятности события
Для математического изучения случайного события необходимо ввести количественную оценку случайности события. Понятно, что одни события имеют больше шансов («более вероятны») наступить, чем другие. Вероятность события
— это численная мера объективной возможности его появления. Т.о. событию можно поставить в соответствие определенное число — его вероятность.
Вероятность случайного события обозначается P(A) . Вероятность — это функция множества.
Таким образом, каждому событию А из алгебры событий F, построенной на множестве Ω, поставим в соответствие число P(A) — вероятность события А, удовлетворяющую следующим аксиомам.
•А1. Аксиома неотрицательности: P(A) ≥ 0. Вероятность любого слу-
чайного события есть неотрицательное число.
•А2. Аксиома аддитивности: P( A + B) = P(A) + P(B) . Вероятность суммы
несовместных событий A и B равна сумме вероятностей этих событий. Вероятность рассматривается как численная мера возможности наступления события при проведении опыта. Главное свойство всякой меры состоит в том, что мера суммы двух объектов без общих элементов равна сумме мер. Для вероятности как меры это свойство является справедливым.
•А3. Аксиома нормировки: P(Ω) = 1. Вероятность достоверного события равна единице.
Определим вероятность случайного события для случая, когда Ω конечное. Пусть F — алгебра, состоящая из всех подмножеств множества Ω. Поставим в соответствие каждому ω из Ω неотрицательное число p(ω ),
которое назовем элементарной вероятностью, т.е. зададим на Ω числовую функцию от аргумента произвольной природы, удовлетворяющую условию
∑ p(ω) = 1.
ωΩ
|
Для любого A из F положим |
|
|
P( A) = ∑ p(ω) . |
(2.1) |
|
ω A |
|
|
Проверим систему аксиом. |
|
A1. |
Аксиома неотрицательности: если вероятность любого элементарного собы- |
|
тия ω Ω неотрицательна p(ω ) ≥ 0 , то P( A ) ≥ 0 . |
|
|
А2. |
Аксиома аддитивности: если AB = , то P( A + B ) = P( A ) + P( B ). |
|

|
|
|
11 |
Действительно, |
P(A + B) = |
∑ p(ω) . Учитывая, что события A и B являются не- |
|
|
|
ω A+B |
|
совместными, |
∑ p(ω) = ∑ p(ω )+ ∑ p(ω ) = P(A) + P(B) . Следовательно, |
||
ω A+B |
ω A |
ω B |
|
P( A + B ) = P( A ) + P( B ). |
|
|
|
А3. Аксиома нормировки: если |
∑ p(ω) = 1, то P( Ω ) = 1. |
||
|
|
|
ωΩ |
Таким образом, определена тройка (Ω, F, P) . Совокупность объектов
( Ω ,F,P), где Ω — ПЭС, F — алгебра событий на множестве Ω, P — вероятность, удовлетворяющая аксиомам А1-А3, называется вероятностным пространством.
Итак, Ω определяется опытом или экспериментом, F — алгебра подмножеств Ω . Единственным компонентом вероятностного пространства, которое требует определения является вероятность P .
Таким образом, в вероятностном пространстве необходимо назначить элементарные вероятности. Это можно сделать, во-первых, исходя из смысла поставленной задачи.
Во-вторых, задать элементарные вероятности как частоту элементарных событий, появляющихся во время проведения одинаковых и независимых повторных испытаний. Произведя достаточно большое количество опытов или испытаний в совершенно одинаковых, за исключением влияния случайного фактора, условиях, можно определить как часто наступает событие А, и вычислить его вероятность (такое определение вероятности будем называть статистическим).
~ |
m |
|
|
P(A) = |
n |
, |
(2.2) |
m — число испытаний, в которых появилось событие A; n — общее число испытаний.
Для надежного определения вероятности нужно проделать большое число испытаний (опытов), что не всегда просто.
В-третьих, можно задать элементарные вероятности, используя некие гипотезы. Например, гипотезу о равных возможностях наступления элементарных событий.
Пусть |
|
p(ω) |
(ω Ω ) |
является константой. Т.к. |
Ω = {ω1,ω2 ,...,ωn }, |
|||||||||||||||
p(ωi ) = 1 = |
|
1 |
, где |
|
|
|
|
Ω |
|
|
|
|
|
|
— |
мощность множества Ω. |
Очевидно, что |
|||
|
|
|
|
|
|
|||||||||||||||
|
|
|
||||||||||||||||||
n |
Ω |
|
|
|
1 |
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
P( A) = ∑ p(ω) = ∑ |
|
|
|
|
= |
|
|
|
|
|
. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Ω |
|
|
|
Ω |
|
|
|
|||||||||||
|
|
|
|
|
|
|||||||||||||||
ω A |
|
ω A |
|
|
|
|
|
|
|
|
|
|||||||||
Если A = m , то

12 |
|
P(A) = m . |
(2.3) |
n |
|
Вероятность события А вычисляется как отношение числа элементарных событий, благоприятствующих этому событию, к общему числу элементарных событий.
Данное определение вероятности называется классическим определением вероятности.
Пример 2.6. В урне 10 пронумерованных шаров с номерами от 1 до 10. Вынули один шар. Какова вероятность того, что номер вынутого шара не превосходит 10? Какова вероятность, что номер вынутого шара больше 10?
Решение. ПЭС Ω = {ω1,ω2,ω3,ω4,ω5,ω6,ω7 ,ω8,ω9,ω10} (событие ωi означает, что в результате опыта вынутый шар соответствует i-му номеру, i = 1,2,…,10). Следовательно n = 10 (см. формулу (2.3)).
Пусть событие А – «номер вынутого шара не превосходит 10». Число случаев благоприятствующих появлению события А равно числу всех возможных случаев m=n=10 ( A = Ω ). Следовательно, событие А является достоверным событи-
ем и Р(А)=1.
Пусть событие В – «номер вынутого шара больше 10». Очевидно, что B = { } и m = 0. Т.о. событие В — невозможное событие и P( B ) = 0. ►
Пример 2.7. Из колоды в 36 карт вынимается одна карта. Какова вероятность появления карты пиковой масти?
Решение. Исходы опыта (вынимание карты из колоды) равновозможны, мощность ПЭС равно 36, т.е. n=36.
Событие А – «появление карты пиковой масти». Число случаев, благоприятствующих появлению события А равно 9 (в колоде 9 карт пиковой масти). Следо-
вательно, P( A ) = 369 = 14 .►
Пример 2.8. Бросаются одновременно две монеты. Какова вероятность выпадения орла на обеих монетах? Какова вероятность того, что решка выпадет хотя бы на одной монете?
Решение. Определим ПЭС. Ω = {ω1 = (о,о),ω 2 = (о, р),ω3 = ( р,о),ω 4 = ( р, р)} («о» — выпал «орел», «р» — выпала «решка»). Т.о. n = 4 .
Событие А — «орел выпал на обеих монетах»: А= {ω1}. Число элементарных исходов, благоприятствующих событию А, равно 1, т.е. m = 1. Следовательно
P( A ) = 14 .
Событие B — «решка выпадет хотя бы на одной монете»: B = {ω 2,ω3,ω 4}.

13
Т.о. m = 3 и P( B ) = 34 . ►
Пример 2.9. Из урны, в которой M белых и N -M чёрных шаров, наудачу, без возвращения вынимают k шаров, k<N. Термин «наудачу» означает, что появление любого набора из k шаров равновозможно. Найти вероятность того, что будет выбрано ровно k1 белых и k - k1 чёрных шаров (событие А).
Решение. Заметим, что при k1 > M или k - k1 > N - M искомая вероятность равна 0, так как соответствующее событие невозможно. Пусть k1 ≤ M. Результатом эксперимента является набор из k шаров. При этом можно не учитывать или учитывать порядок следования шаров.
1. Выбор без учета порядка. Общее число элементарных исходов есть число k –элементных подмножеств множества, состоящего из n элементов, то есть
Ω = СNk .
Обозначим через A событие, вероятность которого требуется найти. Событию A благоприятствует появление любого набора, содержащего k1 белых шаров и k - k1 черных.
Число благоприятных исходов равно произведению числа способов выбрать k1 белых шаров из M и числа способов выбрать k - k1 черных шаров из N - M:
A = СMk1 СNk −−kM1 .
Сk1 Сk −k1
Вероятность события A равна: P(A) = M kN − M .
СN
2. Выбор с учетом порядка. Общее число элементарных исходов есть число способов разместить N элементов на k местах Ω = ANk .
При подсчете числа благоприятных исходов нужно учесть, как число способов выбрать нужное число шаров, так и число способов расположить эти шары среди k. Можно, скажем, посчитать число способов выбрать k1 мест среди k (рав-
ное Сkk1 ), затем число способов разместить на этих k1 местах M белых шаров (равное AMk1 — не забывайте про учет порядка!), и затем число способов разместить на
оставшихся k - k |
1 |
|
местах N - M черных шаров (равное Ak − k1 |
). Перемножив эти |
||||||||
|
|
|
|
|
|
|
|
|
|
N − M |
|
|
числа, получим: |
|
|
А |
|
= Сk1 Ak1 |
Ak −k1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
k M |
|
N − M |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
Сkk1 Ak1 |
Ak −k1 |
Сk1 Сk −k1 |
|
||
Следовательно P( A) = |
|
M |
N − M |
= |
M N − M |
.► |
|
|||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
СkN |
СkN |
|
|||
В рассмотренной задаче мы сопоставили каждому набору из k1 белых и k-k1 черных шаров вероятность получить этот набор при выборе k шаров из урны,
14
содержащей M белых и N-M черных шаров. Очевидно, что если k1 = k и k1 = 0 ,
тоP(A) = |
СkM |
и P(A) = |
СkN − M |
соответственно. |
|
СkN |
СkN |
||||
|
|
|
Пример 2.10. В урне 10 шаров: 6 белых и 4 черных. Вынули два шара. Какова вероятность, что оба шара белые (событие А)?
Решение. Применим схему, приведенную в |
примере |
|
2.9. Тогда n = C 2 |
и |
|||||||
|
C62 |
|
|
|
|
|
|
|
|
10 |
|
m = C62 . Искомая вероятность P(A) = |
= |
|
6!2!8! |
|
= |
5 6 |
= |
1 |
. ► |
|
|
C102 |
10!2!4! |
9 10 |
3 |
|
|||||||
|
|
|
|
|
|
||||||
Пример 2.11. В цехе работают 6 мужчин и 4 женщины. По табельным номерам наудачу отобраны 7 человек. Найти вероятность того, что среди отобранных лиц три женщины (событие А).
Решение. Для решения данной задачи можно также использовать схему, приведенную в примере 2.9. Общее число возможных исходов равно числу способов,
которыми можно отобрать 7 человек из 10, т.е. n = C107 .
Найдем число исходов, благоприятствующих интересующему нас событию: трех женщин можно выбрать из четырех C43 способами; при этом остальные че-
тыре человека должны быть мужчинами, их можно отобрать C64 способами. Сле-
довательно, число благоприятствующих исходов |
m = C3C4 |
. Искомая вероятность |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
4 |
6 |
|
|
C3C 4 |
4!6!7!3! |
|
|
3 4 5 6 |
|
1 |
|
|
|
|
||
P(A) = |
4 6 |
= |
|
|
|
= |
8 9 10 |
= |
|
. ► |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
C107 |
1!3!4!2!10! |
|
|
2 |
|
|
|
|
||||
Пример 2.12. Из множества перестановок чисел 1,2,...,n |
наугад выбирается одна. |
||||||||||||
Какова вероятность, что числа 1,2,...,m < n стоят рядом в любом порядке (событие В), в порядке возрастания (событие А)?
Решение. По условию задачи ПЭС — это множество всех перестановок из n элементов, Ω = n!. Для определения A объединим эти m чисел в одно число α и
рассмотрим (n − m + 1)! перестановок нового множества {α , m + 1, m + 2,..., n}.
Очевидно, A = (n − m + 1)! и P(A) = (n − m + 1)! . n!
Числа, входящие в объединенное число α , можно представлять m! спосо-
бами, следовательно, B = A m! и P(B) = (n − m + 1)!m! . ► n!
Пример 2.13. Пять книг расставляются на полку. Найти вероятность того, что две определенные книги окажутся рядом (событие А).

15
Решение. Для решения задачи можно применить схему, приведенную в приме-
ре 2.12.
Число всех способов, которыми можно расставить на полке пять книг, равно числу перестановок из пяти элементов n = Ω = A55 = 5! и m = A = 2! 4!. Итак,
P(A) = 2!5!4! = 0,4 .►
Пример 2.14. В лифт 9-тиэтажного дома вошли 4 человека. Каковы вероятности следующих событий: все четверо выйдут на одном этаже; все четверо выйдут на разных этажах?
Решение. Опыт состоит в том, что люди выходят из лифта произвольным образом: каждый из четырех человек может выйти на любом из восьми этажей (со второго по девятый). Общее число исходов этого опыта n = 84 (первый человек может выйти на любом из восьми этажей, второй - также на любом из восьми этажей и т.д.; имеем размещения с повторениями из множества {2, 3,…,9}).
Пусть событие А состоит в том, что все 4 человека выйдут на одном и том же этаже, тогда число исходов описанного опыта, благоприятствующих наступ-
лению события А, равно 8. Поэтому, P(A) = 884 = 813 ≈ 0,002 .
Пусть событие В состоит в том, что все 4 человека выйдут на разных этажах, тогда число исходов опыта, благоприятствующих наступлению события В,
равно A84 = 8 7 6 5 (у первого пассажира есть 8 возможностей выйти, тогда у
второго — 7 возможностей, у третьего — 6 и у четвертого — 5). Тогда
P(A) = 8 7846 5 ≈ 0,41. ►
Пример 2.15. Наудачу взятый телефонный номер без нуля впереди состоит из 7 цифр. Найти вероятность того, что все цифры различны.
Решение. Событие А состоит в том, что в наудачу набранном телефонном номере все цифры будут различны. Поскольку первая цифра не ноль, то для выбора первой цифры существует 9 вариантов. Каждая из последующих 6 цифр может быть выбрана 10 способами. Число всех различных номеров равно n = 9 106 . Число номеров с различными цифрами равно m = 9 9 8 7 6 5 4 = 9 A96 (первую
цифру можно выбрать 9 способами, вторую —9, третью — 8, четвертую — 7 и
|
6 |
|
|
т.д.). Тогда P(A) = |
9 A9 |
≈ 0,06 |
. ► |
6 |
|||
|
9 10 |
|
|
2.4. Свойства вероятностей. Теорема сложения вероятностей
Приведенные выше аксиомы позволяют доказать ряд теорем и свойств вероятностей.

16
Из аксиом А1-А3 нетрудно доказать следующие свойства вероятностей:
•С1. вероятность невозможного события равна нулю: P( ) = 0;
•С2. вероятность любого события не превосходит единицы: P( A) ≤ 1;
•С3. если событие А влечет событие В, т.е. A B , тоP( A) ≤ P(B) ;
•С4. вероятность суммы двух событий не превышает суммы вероятностей этих событий: P(A + B) ≤ P(A) + P(B) ;
• С5. сумма вероятностей противоположных событий равна единице:
P(A) + P(A) = 1.
Как известно, вероятность суммы двух несовместных событий определяется аксиомой А2:
Р(А+В)=Р(А)+Р(В), A B = . |
(2.4) |
|||
Заметим, что формула (2.4) справедлива для любого числа несовместных |
||||
событий A1, A2 ,..., An : |
|
|
|
|
|
n |
|
n |
(2.5) |
P |
∑ Ai |
= ∑ P(Ai ) . |
||
i=1 |
|
i=1 |
|
|
Тогда, сумма вероятностей |
событий A1, A2 ,..., An , образующих |
полную |
||
группу, равна единице: |
|
|
|
|
P(A1 ) + P(A2 ) + ... + P(An ) = 1. |
(2.6) |
|||
Является справедливой следующая теорема сложения вероятностей. Ве-
роятность суммы двух событий равна сумме вероятностей этих событий без вероятности их совместного наступлении:
P(A + B) = P(A) + P(B) − P(A B) . |
(2.7) |
Пример 2.16. В урне 10 белых, 15 черных, 20 синих и 25 красных шаров. Вынули один шар. Найти вероятность того, что вынутый шар а) синий или черный; б) белый или черный или синий.
Решение. Обозначим следующие события:
A– «вынули белый шар»: P(A) = 1070 ;
B– «вынули черный шар»: P(B) = 1570 ; С – «вынули синий шар»: P(C) = 7020 ;
D– «вынули красный шар»: P(D) = 7025 .
