
Теория_Вероятностей_КР7
.pdf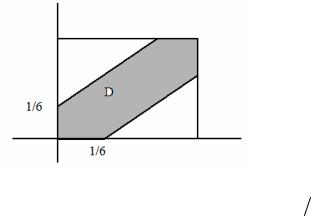
37
y
x |
|
|
|
|
|
|
|
|
Рис.11. |
|
|
|
|
− (5 6)2 |
|
|
|
Искомая вероятность определяется с.о. P( A) = |
S |
D |
= |
1 |
= |
11 |
. ► |
|
|
|
1 |
36 |
|||||
|
SΩ |
|
|
|
|
|||
5.Случайные величины
5.1.Понятие случайной величины. Функция распределения
Понятия случайного события не достаточно для описания результатов наблюдений некоторых величин, имеющих числовое выражение. Например, при анализе прибыли предприятия в первую очередь интересуются ее размерами. Поэтому понятие случайного события дополняется понятием случайной величины. Под случайной величиной понимается переменная величина, которая в зависимости от исхода испытания принимает одно из возможного множества своих значений.
Примеры случайных величин:
1.число очков, выпавших при бросании игральной кости,
2.объем продаж в следующем квартале,
3.число покупателей, подходящих к расчетному окну в супермаркете за час,
4.число произведенных выстрелов до первого попадания,
5.время безотказной работы прибора,
6.расход электроэнергии на предприятии за месяц.
Случайные величины будем обозначать заглавными буквами латинского алфавита — X, Y, Z,…, а их возможные значения — соответствующими малыми буквами — x, y, z, …
Случайная величина называется дискретной, если множество ее значений конечно, или бесконечное, но счетное.
Под непрерывной случайной величиной будем понимать величину, бесконечное несчетное множество значений которой есть некоторый интервал (конечный или бесконечный) числовой оси.
Так, в приведенных выше примерах1-4 имеем дискретные случайные величины (в примерах 1-3 — с конечным множеством значений; в примере 4 — с бес-
38
конечным, но счетным множеством значений); а в примерах 5 и 6 — непрерывные случайные величины.
Дадим теперь строгое определение случайной величины, исходя из теоре- тико-множественной трактовки основных понятий теории вероятностей.
Введем понятие σ-алгебры в дополнение к определению алгебры (см.
п. 2.2). Алгебра множеств S, содержащая бесконечное число элементов, называ-
∞
ется σ-алгеброй, если из An S , п = 1,2,3,..., следует ∑ An S .
n=1
Пусть ( Ω , F, P) — произвольное вероятностное пространство. Ω — произвольное пространство элементарных событий, F — σ-алгебра случайных событий, P — вероятность, удовлетворяющая аксиомам А1,А3 и
аксиоме счетной аддитивности: |
∞ |
|
∞ |
P ∑ Ai |
= ∑ P ( Ai ) для любой последовательности |
||
|
i=1 |
|
i=1 |
попарно несовместных событий.
Случайной величиной (СВ) называется действительная числовая функция X = X (ω), ω Ω , такая что при любом действительном x событие
{ω : X (ω) ≤ x} принадлежит F. |
(5.1) |
Условие (5.1) означает, что подмножество |
множества Ω, на котором |
X (ω) ≤ x , принадлежит σ-алгебре случайных событий F, т.е. является случайным событием. Это событие будем записывать в виде {X ≤ x}, а его вероятность —
P(X ≤ x) .
Функцией распределения случайной величины X называется функция
F(x) = P(X ≤ x) , |
(5.2) |
заданная на всей числовой прямой ( x R ).
Основные свойства функции распределения
1.Функция распределения случайной величины есть неотрицательная функция, заключенная между нулем и единицей: 0 ≤ F(x) ≤ 1.
2.F(x) – неубывающая функция на всей числовой оси, т.е. если х1< х2, то
F(x1)≤ F(x2).
3. |
Функция распределения непрерывна справа: lim F(x) = F(x0 ) . |
|
|
|
x→ x0 + 0 |
4. |
На минус бесконечности функция распределения равна нулю, на плюс |
|
бесконечности равна единице: lim F(x) = 0 , |
lim F(x) = 1. |
|
|
x→−∞ |
x→+∞ |
Знание функции распределения случайной величины дает возможность вычислять вероятности событий, связанных с этой СВ.
Если F(x) — функция распределения с.в. X , то при a < b

39 |
|
P(a < X ≤ b) = F(b) − F(a) , |
(5.3) |
Равенство (5.3) нетрудно доказать.
◄ При a < b событие {X ≤ b} можно представить, как сумму событий {X ≤ a} и {a < X ≤ b}, т.е. {X ≤ b}={X ≤ a} {a < X ≤ b}. Слагаемые в правой части этого равенства являются несовместными случайными событиями. Следовательно P(X ≤ b) = P(X ≤ a) + P(a < X ≤ b) . Откуда получаем равенство (5.3). ►
Из всего многообразия случайных величин будем рассматривать два класса случайных величин: дискретные и абсолютно непрерывные случайные величины.
5.1.1. Дискретная случайная величина
Дискретной случайной величиной называют случайную величину, множество значений которой конечно или счетно.
Приведем пример построения дискретных случайных величин на ПЭС. Пример 5.1. С двукратным подбрасыванием монеты свяжем следующие события:
X— число выпадающих гербов,
Y— число выпадающих решек,
Z=X-Y.
Тогда Ω = {ω1(ГГ),ω2 (ГР),ω3 (РГ),ω4 (РР)}. Функции X, Y, Z можно опре-
делить следующей таблицей
Ω |
X |
Y |
Z |
ω1 |
2 |
0 |
2 |
ω2 |
1 |
1 |
0 |
ω3 |
1 |
1 |
0 |
ω4 |
0 |
2 |
-2 |
Т.о. мы задали три функции на ПЭС для всякого ω Ω . ►
Поведение дискретной случайной величины X может задаваться таблицей, в первой строке которой перечислены все возможные значения случайной величины, а во второй — вероятности, с которыми она принимает эти значения:
|
xi |
x1 |
x2 |
|
K |
xn |
|
K |
|
|
pi |
p1 |
p2 |
|
K |
pn |
|
K |
|
|
|
||||||||
|
То, что случайная величина Х принимает одно из значений x1 , x2 , …, xn ,… |
||||||||
|
есть достоверное событие и поэтому должно выполняться равенство |
|
|
||||||
|
∞ |
|
|
|
|
|
|
|
|
|
∑ pk = 1, (в случае в случае конечного множества значений |
|
|
||||||
|
k =1 |
|
n |
|
|
|
|
(5.4) |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ pk |
= 1). |
|
|
|
|
|
k =1

40
Закон распределения может быть задан графически в виде многоугольника распределения вероятностей, т.е. в виде ломаной, соединяющей точки (хk, рk) (см.
рис.12).
Рис.12
Пример 5.2. Переменная величина Х есть число очков, выпадающее на верхней грани игральной кости при ее однократном бросании. Составить закон распределения этой случайной величины.
Решение. Так как любое число очков при однократном бросании кости выпада-
ет с вероятностью P = 16 , то закон распределения случайной величины имеет вид:
xi |
1 |
2 |
3 |
4 |
5 |
6 |
pi |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
1/6 |
6
Убедимся, что ∑ pi = 1. ►
i=1
Пример 5.3. Вероятность попадания при каждом выстреле р=0,8. Имеется три снаряда. Определить вероятность того, что будет израсходован один снаряд, два снаряда, три снаряда, если стрельба ведется до первого попадания или промаха всеми тремя снарядами. Составить закон распределения случайной величины Х – числа израсходованных снарядов.
Решение. Пусть Х – число израсходованных снарядов. Случайная величина X может принимать значения 1, 2, 3.
Обозначим P( X = xk ) вероятность того, что будет израсходовано xk снаря-
дов.
Тогда Р(X=1)=0,8 (произошло попадание при первом выстреле), Р(X=2)=(1-р)р=0,16 (первый выстрел промах, второй выстрел попадание), Р(X=3)=(1-р)2=0,04 (все три выстрела промах).
Закон распределения случайной величины X будет иметь вид:
41
xk |
1 |
2 |
3 |
pk |
0,8 |
0,16 |
0,04 |
►
Пример 5.4. Экзаменатор задал студенту 4 дополнительных вопроса. Вероятность того, что студент ответит на любой заданный вопрос 0,9. Составить закон распределения случайной величины Х – числа ответов на заданные вопросы.
Решение. По условию Х – число ответов на заданные 4 вопроса. Понятно, что число ответов может быть равно 0, 1, 2, 3, 4.
Для вычисления вероятностей события X = xk |
( xk = 0,1,2,3,4 ) используем |
|||||||
формулу Бернулли P (k) = Ck pk qn−k . |
|
|
|
|
|
|||
|
n |
|
n |
|
|
|
|
|
Здесь n=4, р=0,9, q=0,1. |
|
|
|
|
|
|||
P( X = 0) = q4 = 0,14 , |
|
|
|
|
|
|||
P( X = 1) = C41 p1q3 |
= 4 0,9 0,13 , |
|
|
|
|
|
||
P( X = 2) = C42 p2 q2 |
= 6 0,92 0,12 , |
|
|
|
|
|
||
P( X = 3) = C43 p3 q = 4 0,93 0,1, |
|
|
|
|
|
|||
P( X = 4) = p4 = 0,94 . |
|
|
|
|
|
|||
Закон распределения СВ X будет иметь вид: |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
xk |
0 |
|
1 |
2 |
|
3 |
4 |
|
pk |
0,0001 |
|
0,0036 |
0,0486 |
|
0,2916 |
0,6561 |
|
►
Пример 5.5. Производится серия независимых опытов, в каждом из которых наступает событие А с одной и той же вероятностью p . Опыты продолжаются до первого появления события А. Рассматривается случайная величина X — число произведенных опытов. Составить для нее закон распределения.
Решение. Указанная случайная величина X |
может принимать значения |
x1 = 1, x2 = 2, x3 = 3,... . Событие X = n (n = 1,2,3,...) |
означает, что в первых n − 1 |
опытах событие А не наступает, а в n-м наступает. Вероятность такого исхода рав-
на: q q ... q p = p qn−1 |
, где q = 1 − p . |
14243 |
|
n−1 раз |
|
Т.о. закон распределения случайной величины X можно записать в виде следующей таблицы.
xi |
1 |
2 |
K |
n |
K |
pi |
p |
pq |
K |
p qn−1 |
K |

42
Заметим, что условие (5.4) в данном случае выполнено. Действительно,
∞
принимая во внимание условие сходимости геометрического ряда ∑aqn−1
n=1
( q < 1) и формулу S = 1 −a q для его суммы, получаем
∞ |
p |
|
|
∑ pqn−1 = |
= 1. ► |
||
1 − q |
|||
n=1 |
|
Ряд распределения служит исчерпывающей характеристикой распределения вероятностей дискретной случайной величины. Это означает, что вероятность любого события, связанного с данной случайной величиной, может быть найдена, если задан ряд распределения. В частности, ряд распределения с.в. X однозначно определяет ее функцию распределения F(x).
Прежде, чем привести явное выражение для F(x), рассмотрим следующий пример.
Пример 5.6. Из прошлых данных известно, что компания в течение 20 кварталов 4 квартала имела доход 10 млн. руб., 8 кварталов — 5 млн. руб., 5 кварталов — 1 млн.руб., и 3 квартала компания имела убытки в размере 4 млн. руб. Построим закон распределения для случайной величины X — дохода компании за квартал.
Решение. Очевидно, что с.в. X может принимать значения: -4, 1, 5, 10. Для того чтобы найти вероятности значений с.в. используем статистическое определение вероятности (см. формулу (2.2)). Тогда закон распределения случайной величины X можно записать в виде таблицы.
xi |
-4 |
1 |
5 |
10 |
pi |
3 20 |
5 20 |
8 20 |
4 20 |
или |
|
|
|
|
|
|
|
|
|
xi |
-4 |
1 |
5 |
10 |
pi |
0,15 |
0,25 |
0,40 |
0,20 |
Это распределение вероятности легко использовать для вычисления вероятностей всех событий, связанных с доходом.
Вероятность получения дохода в размере 5 млн. рублей и более можно найти следующим образом: 0,20+0,40=0,60.
Для функции распределения случайной величины X имеем:
при x < −4 F(x) = P(X ≤ x) = P( ) = 0 ;
при − 4 ≤ x < 1 F(x) = P(X ≤ x) = P(X = −4) = 0,15 ;
при 1 ≤ x < 5 F(x) = P(X ≤ x) = P({X = −4} {X = 1}) = 0,4 ;
при 5 ≤ x < 10 F(x) = P(X ≤ x) = P({X = −4} {X = 1} {X = 5}) = 0,8;
43
при x ≥ 10 F(x) = P(X ≤ x) = P({X = −4} {X = 1} {X = 5} {X = 10}) = 1.
|
0, если x < −4; |
|
|
0,15, если − 4 ≤ x < 1; |
|
|
0,40, если1 ≤ x < 5; |
Итак F(x) = |
|
|
0,80, если 5 ≤ x < 10; |
|
|
|
1, если10 ≤ x. |
|
|
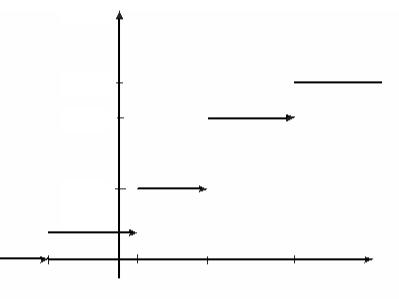
На рис.13 представлен график функции распределения случайной величины X. ►
F(x)
1
0.8
0.4
0,15
-4 |
|
1 |
|
5 |
|
10 |
|
x |
Рис. 13.
Для дискретной случайной величины функция распределения находится по формуле
F(x) = ∑ pk , |
(5.5) |
xk ≤ x |
|
Функции распределения дискретных случайных величин являются разрывными ступенчатыми функциями.
5.1.2. Непрерывная случайная величина
Случайная величина X, заданная на вероятностном пространстве ( Ω , F, P) называется абсолютно непрерывной случайной величиной если существует такая функция f = f (x) (x R ), называемая плотностью распределения ве-
роятностей случайной величины, что функция распределения вероятностей
x |
|
F(x) = ∫ f (t) dt . |
(5.6) |
−∞
Далее такую случайную величину будем называть непрерывной случайной величиной, поскольку это не вызовет противоречия в понимании изложенного материала.
44
Очевидно, что функция распределения F(x) непрерывной случайной величины является непрерывной в любой точке.
Плотность распределения непрерывной случайной величины Х обладает следующими свойствами:
1. Плотность распределения f(x) – неотрицательная функция, т.е. |
|
f(x) ≥ 0. |
(5.7) |
2. Интеграл по бесконечному промежутку (−∞,+∞) от плотности распределения f(x) равен единице:
+∞ |
(5.8) |
∫ f (x)dx = 1. |
−∞
3. В точках дифференцируемости функции распределения F(x) ее производная равна плотности распределения:
f (x) = F ′(x) . |
(5.9) |
4. Вероятность попадания непрерывной случайной величины в интервал (a,b] равна определенному интегралу от ее плотности вероятности в пределах от a до b, т.е.
b |
(5.10) |
P(a < X ≤ b) = ∫ f (x)dx . |
a
Приведем важное утверждение без доказательства: вероятность любого отдельно взятого значения непрерывной случайной величины равно нулю.
P(X = a) = 0. |
(5.11) |
Из приведенного выше факта следует, что нулевой вероятностью могут обладать и возможные события, т.к. событие, состоящее в том, что случайная величина X приняла конкретное значение а, является возможным. Другими словами, появление любого отдельного значения непрерывной случайной величины является возможным событием, несмотря на то, что вероятность его появления равна нулю.
Однако, представление о событии, имеющем отличную от нуля вероятность, но складывающемся из событий с нулевой вероятностью, не более парадоксально, чем представление об отрезке, имеющем определенную длину, тогда как ни одна точка отрезка отличной от нуля длиной не обладает. Отрезок состоит из таких точек, но его длина не равна сумме их длин.
Т.о. для непрерывной случайной величины верны следующие равенства
P(a < X ≤ b) = P(a ≤ X < b) = P(a ≤ X ≤ b) = P(a < X < b) . |
(5.12) |
Пример 5.7. Случайная величина Х задана функцией распределения

|
|
45 |
|
|
|
0, |
при x < 2, |
F(x) = |
(x − 2)2 |
, при 2 ≤ x < 3, |
|
|
|
|
|
|
|
1, |
при x ≥ 3. |
|
|
||
Найти плотность распределения этой случайной величины и вероятность попадания ее в интервал (1; 2,5).
Решение. По формуле (5.9)
|
|
|
|
0 |
при |
x < 2, |
|
|
||||
|
|
|
|
|
при 2 ≤ x < 3, |
|
|
|||||
|
|
f (x) = F′(x) = 2(x − 2) |
|
|
||||||||
|
|
|
|
0 |
при x ≥ 3. |
|
|
|||||
|
|
|
|
|
|
|||||||
Проверим свойство 2 плотности распределения. |
|
|
||||||||||
+∞ |
2 |
3 |
+∞ |
|
x |
2 |
|
|
3 |
9 |
|
|
|
|
|
||||||||||
|
|
|
|
|
||||||||
∫ f (x)dx = ∫ 0dx +∫ 2(x − 2)dx + ∫ 0dx = 2( |
|
− 2x) |
|
= 2( |
− 6 − 2 + 4) = 1. |
|||||||
|
|
2 |
||||||||||
−∞ |
−∞ |
2 |
|
3 |
2 |
|
|
2 |
|
|||
|
|
|
|
|
|
|
|
|||||
Требуемая вероятность будет равна (см. формулы (5.3), (5.12))
P(1 < X < 2,5) = F(2,5) − F(1) = 14 − 0 = 14 . ►
Пример 5.8. Дана плотность распределения непрерывной случайной величины Х:
|
|
|
|
|
|
0 |
при |
x < 1, |
|
|
|
|
|
|
||
|
|
|
f (x) = |
|
|
при 1 ≤ x < 2, |
|
|
|
|||||||
|
|
|
x − 1 |
|
|
|
||||||||||
|
|
|
|
|
|
2 |
при x ≥ 2. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
||||
Найти функцию распределения этой величины. |
|
|
|
|
||||||||||||
Решение. Используем формулу |
(5.6). |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если х < 1, |
F(x) = ∫ 0dt = 0 . |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
−∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если 1 ≤ x < 2, то |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
||
x |
|
1 |
x |
|
1 |
t 2 |
|
1 |
|
|
|
1 |
|
2 |
||
|
|
|
|
|
|
|||||||||||
F(x) = ∫ f (t)dt = ∫ 0dx + ∫ |
t − |
|
|
− |
|
|
|
|
= |
|
(x − x). |
|||||
dt = |
2 |
t |
|
|
|
|||||||||||
−∞ |
|
−∞ |
1 |
|
|
2 |
2 |
|
|
|
1 |
|
2 |
|
||
|
|
|
|
|
|
|
|
|
|
|
||||||
Если х ≥ 2, |
то |
|
|
|
|
|
|
|
|
|
(x |
|
− x) |
2 |
||
x |
|
1 |
2 |
|
|
1 |
x |
|
|
1 |
2 |
|||||
|
− |
|
|
= 1. |
||||||||||||
F(x) = ∫ f (t)dt = ∫ 0dt + ∫ |
x |
dx + ∫ 0dx = |
|
|
||||||||||||
−∞ |
|
−∞ |
1 |
|
|
2 |
2 |
|
|
2 |
|
|
|
|
|
1 |
Итак, искомая функция распределения имеет вид |
|
|
|
|||||||||||||
|
0 |
при |
x < 1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
F(x) = 1 (x2 − x) при 1 ≤ x < 2, ► |
|
|
|
|
|
|
|
|
|
|
||||||
2 |
1 |
при x ≥ 2. |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
46
5.2. Функции случайного аргумента
Для дальнейшего изложения материала введем понятие независимых случайных величин.
Две случайные величины называются независимыми, если закон распределения вероятностей одной из них не зависит от того, какие возможные значения приняла другая величина.
Согласно данному определению, две дискретные случайные величины X и Y независимы, если события (X = xi ) и (Y = y j ) независимы для всех значений xi и
y j , в частности
P((X = xi ) (Y = y j )) = P(X = xi ) P(Y = y j ) . |
(5.13) |
Рассмотрим задачу построения законов распределения функций от случайных величин.
Если каждому возможному значению случайной величины X по определенному правилу поставлено в соответствии одно возможное значение случайной ве-
личины Y, то Y называют функцией случайного аргумента X: Y = g(X).
Рассмотрим сначала случай, когда аргумент X – дискретная случайная величина с возможными значениями х1 ,х2 ,..., хn, вероятности которых соответственно равны р1,р2,...,рп. Очевидно, Y – также дискретная случайная величина с возможными значениями y1 = g(x1), y2 = g(x2 ),..., yn = g(xn ) , некоторые возможные зна-
чения при этом могут совпадать. Оставим только различные возможные значения случайной величины Y : y1, y2 ,..., ym . Пусть g−1 ( yi ) - прообраз возможного значения
yi , т.е. g−1 ( yi ) = {xk : yi = g (xk )} , тогда при записи закона распределения вероятностей функции Y руководствуются следующим равенством:
P(Y = yi ) = ∑ P(X = xk ) . |
(5.14) |
xk g−1 ( yi ) |
|
Пример 5.9. Дискретная случайная величина X задана законом распределения
xk |
-2 |
-1 |
0 |
1 |
2 |
pk |
0,1 |
0,2 |
0,15 |
0,25 |
0,3 |
Найти закон распределения случайных величин Y = X 2 , Z = 3X .
Решение. Квадрат случайной величины X – это новая случайная величина Y, которая с теми же вероятностями, что и случайная величина X , принимает значения, равные квадратам ее значений.
Квадраты случайной величины X равны: (−2)2 = 4, (−1)2 = 1, (0)2 = 0 ,
(1)2 = 1, (2)2 = 4 , т.е. величина Y принимает значения 0, 1, 4.
Закон распределения случайной величины Y можно записать в виде.
