Karmanov_Trojanov

Глава 1. Связанные состояния в ступенчатом потенциале

(решение систем линейных уравнений)

Поиск уровней энергии частицы в заданном одномерном потенциальном поле обычно сводится к решению задачи о собственных значениях для стационарного уравнения Шредингера [1-2]

−h2 d2 Ψ(x) + V(x) Ψ(x) = E Ψ(x) 2 m dx2

при дополнительных условиях непрерывности волновой функции и ее первой производной, а также условии квадратичной интегрируемости (нормировки) волновой функции.

Подобные задачи возникают при анализе свойств низкоразмерных квантовых систем, таких как квантовые точки, нити или кольца, во многих областях науки и нанотехнологии, связаных с развитием вычислительной техники, физики атомных и молекулярных кластеров, полимерных цепочек и нанокристаллов [3–5].

Одномерная потенциальная решетка

Для потенциалов, ограниченных снизу (V(x) > V0 ) и стремящихся к конечному пределу при x –> ± ∞ , собственные значения дискрет-

ны и принадлежат интервалу [V0<E<Vc], где Vc = min(V(- ∞),V(+ ∞)).

Одно из возможных представлений потенциала в одномерной цепочке атомов состоит в использовании кусочно-постоянных функций. Для этого область действия потенциала разбивается на несколько участков, в пределах которых потенциал считается постоянным,

3

а решение уравнения Шредингера представляется в виде линейной комбинации бегущих вправо и влево плоских волн при условии, что собственное значение El больше высоты ступеньки на данном участке Vn , или экспоненциально убывающих и нарастающих функций при El < Vn :

Если El = Vn , то на этом участке волновая функция представляется прямой линией

Ψ(x)ln = Aln + Bln x

Из условия нормировки следует, что коэффициенты Al1 и BlN обращаются в ноль, поскольку волновая функция связанного состояния должна экспоненциально убывать при x –> ± ∞.

Требование непрерывности волновой функции и ее производной во внутренних точках xn области определения потенциала приводит к системе 2(N+1) линейных уравнений относительно коэффициентов Aln и Bln волновой функции:

Получаемая система уравнений является однородной и потому имеет нетривиальное решение, если определитель D(E ) ее матрицы С обращается в ноль. Решение этого уравнения в общем случае можно получить только численно. Найденные корни этого уравнения определяют спектр частицы в заданном потенциале. После решения уравнения |D(E)| = 0 и нахождения уровней энергии для определения коэффициентов волновой функции необходимо решить представленную выше систему уравнений с учетом дополнительного условия нормировки волновой функции.

4

В качестве примера применения этого метода рассчитаем уровни энергии и волновые функции электрона в системе из No= 5 одинаковых потенциальных ям конечной глубины, разделенных равновысокими барьерами постоянной ширины. Пусть

20

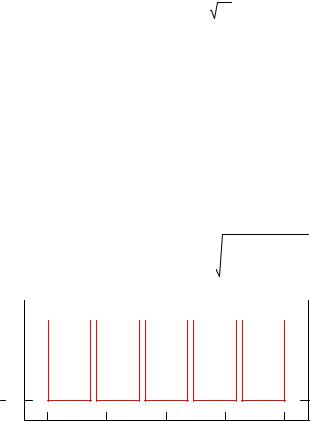
Рис. 1. Потенциальная решетка

Матрицу С(Е) нужной структуры и ее определитель можно сформировать с помощью следующей подпрограммы, а затем рассчитать зависимость его модуля от энергии.

5

e

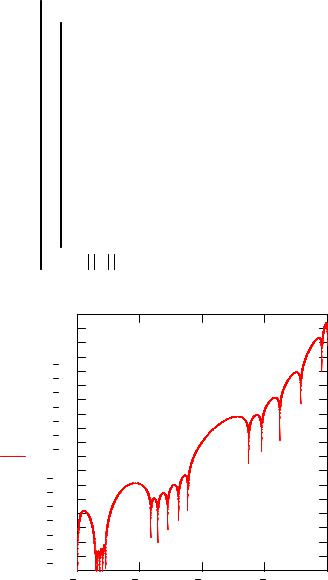
Рис. 2. График функции D(E)

6

Как видно из рис.2, в нашей одномерной решетке формируется система пяти близко расположенных уровней, разделенных промежутком, в котором нет связанных состояний. С увеличением энергии группа из пяти уровней повторяется, а расстояние между уровнями внутри группы увеличивается. Начальные значения энергии, необходимые для начала итерационного уточнения корней с использованием встроенной функции root(), могут быть найдены, например, с помощью следующей программной единицы на основе анализа изменения знака и значений функции в окрестности корня.

En(En,Em,δE) := n ← 0 E ← En

D1 ← D(E)

D2 ← D(E + δE) while E < Em

E ← E + δE

D3 ← D(E) δ1 ← D2 − D1 δ2 ← D3 − D2

if (δ1 δ2 < 0) (δ1 < δ2)

Aen ← E − δE n ← n + 1

D1 ← D2

D2 ← D3

Ae

7

После вычисления уровней энергии следует найти коэффициенты A и B волновых функций для каждого из найденных значений энергии. Для этого следует модифицировать исходную систему линейных уравнений, полагая один из коэффициентов известным, например, равным единице. В дальнейшем расчете его можно найти из условия нормировки волновой функции. Для решения системы уравнений воспользуемся встроенной функцией lsolve().

8

Распечатаем найденные значения уровней энергии и коэффициенты волновой функции для основного состояния системы. Эти коэффициенты являются либо действительными, либо комплексно-сопряжен- ными, что обеспечивает действительность волновой функции состояния.

Волновую функцию задаем с помощью программного блока:

ψ(x,E,ab) := B0 ← 1

for j 1 .. N

break if (Xj−1 ≤ x) (x ≤ Xj)

y ← ab2 j−2 exp(i k(E, j) x) + ab2 j−1 exp(−i k(E, j) x) y ← B0 exp(−i k(E,0) x) if x ≤ X0

y ← ab2 N exp(i k(E,N + 1) x) if x ≥ XN y ← 2 y

9