Karmanov_Trojanov

Какими должны быть параметры потенциала для того, чтобы в яме могли "разместиться" N уровней одинаковой четности?

2. Исходя из определения матриц и используя символьный процессор MathCAD, получите приведенные в упр. 1 уравнения для нахождения уровней энергии в яме конечной глубины.

3. Рассчитайте уровни энергии частицы в потенциальной яме конечной глубины, помещенной в бесконечно глубокую потенциальную яму. Проанализируйте изменения в расположении уровней при увеличении ширины внешней ямы. Результаты сравните с [9].

4.Для выбранных в данной задаче параметров потенциала (a,b,Uo) рассчитайте уровни энергии частицы в системе из двух одинаковых потенциальных ям , решая приведенные в тексте задачи уравнения. Каковы четности волновых функций рассчитываемых состояний?

5.Исходя из определения матриц и используя символьный процессор MathCAD, получите приведенные в тексте задачи уравнения для нахождения уровней энергии в системе из двух близко расположенных одинаковых потенциальных ям конечной глубины.

6.Используя символьный процессор MathCAD, получите аналитическое выражение для коэффициента A4.

7.Рассчитайте волновую функцию нечетного состояния системы

сэнергией e = e11.

8.Проанализируйте зависимость волновой функции четного и нечетного состояний при изменении ширины барьера.

9.Рассчитайте зависимость положения уровней энергии и волновой функции четного и нечетного состояний от высоты барьера.

10.Рассчитайте зависимость положения уровней энергии и волновой функции состояний от параметра непроницаемости барьера, пропорционального произведению ширины и высоты барьера.

11.Предположим, что бесконечно глубокая симметричная потенциальная яма разделена на две равные части потенциальным барьером с переменной шириной и высотой. Рассчитайте зависимость положения уровней энергии и волновой функции состояний от параметра непроницаемости барьера, пропорционального произведению ширины и высоты барьера. Проанализируйте предельный

случай δ - образного барьера (см.[9]).

70

Глава 8. Фазовые переходы в сплавах замещения

(минимизация функции одной переменной)

Существует целый класс дискретных систем с двоичным способом фиксации состояния в каждом узле пространственной решетки, таких как ферромагнетик и антиферромагнетик в модели Изинга, модель решетчатого газа и т.д., формальное микроскопическое описание которых может быть основано на анализе изинговского гамильтониана [16,17] с последующим переходом на уровень макроскопической термодинамики.

Одним из наиболее интересных эффектов, реализующихся в таких системах, являются фазовые переходы, например, упорядочение атомов в сплавах замещения [13,14]. Следуя работе [14], рассмотрим в приближении Брегга – Вильямса изменение состояния сплава со структурой объемно центрированной (ОЦК) решетки. В этом случае из N узлов N/2 узлов можно отнести к α-типу (они расположены в вершинах куба) и N/2 узлов – к β- типу (они расположены в центре куба). В такой решетке число ближайших β-соседей для α-решетки равно z = 8 и наоборот.

Конфигурационная энергия и энтропия

Конфигурационная энергия сплава при учете взаимодействия только ближайших соседей имеет вид

U = Naa Uaa + Nab Uab + Nbb Ubb ,

где Naa, Nab, Nbb и Uaa, Uab, Ubb – число пар атомов каждого типа

и энергии взаимодействия между соседними атомами. Среди zNa соседей атомов типа А будут Nab атомов типа B и 2Naa – атомов типа A и наоборот. Тогда

где Nab(α ,β) – число пар AB, в которых атом А находится в узле α,

а атом B– в узле β, Paα – вероятность замещения узла α атомом А.

71

Если ввести параметр порядка p по правилу [14] p = 2(Paα − Ca),

где Ca – доля узлов типа А, то p = 1 при Ca = 0.5 и Paα= 1, т.е. в

случае, когда все узлы типа α заняты атомами сорта А (полный порядок), и p = 0, если атомы обоих сортов равномерно заселяют узлы

Конфигурационная энтропия при заданном составе и упорядочении

Конфигурационная часть свободной энергии равна

F = U − T S .

Выделяя в этом соотношении часть, зависящую от параметра порядка, и отнеся ее к энергии, равной 0.5NkT, получаем

72

Температура фазового перехода и теплоемкость

Равновесная конфигурация сплава при данной температуре будет соответствовать минимальной свободной энергии как функции параметра порядка. Условие экстремума функции Fp (...) по переменной p – обращение в ноль ее производной. Это условие приводит к трансцендентному уравнению вида

Разлагая левую часть уравнения в ряд по параметру p и учитывая его малость в окрестности точки фазового перехода, сохраняем только линейные члены разложения и получаем для температуры перехода соотношение

Tc = −z ω Ca (1 − Ca) . k

Максимальное значение получается для сплава при Ca = Cb = 0.5

Tcmax = −2 ω . k

Теплоемкость определяется как производная энергии взаимодействия по температуре при постоянном объеме и вблизи точки фазового перехода равна

Величина скачка теплоемкости вблизи точки фазового перехода

Для сплава стехиометрического состава (Ca = Cb = 0.5)

При приближении к точке фазового перехода параметр порядка уменьшается постепенно и не испытывает скачков, а теплоемкость имеет разрыв. Отсюда ясно, что фазовые переходы порядок - беспорядок в сплавах с ОЦК – решеткой – переходы второго рода.

73

Сплав стехиометрического состава

Как пример рассмотрим сплав Cu-Zn (β - латунь) с 50%-ным содержанием меди и цинка, основные параметры которого равны ([13,18])

fp(p,T) := z ω p2 + 2 (Sa(0.5,p) + ln(2)) 4 k T

Условие экстремума этой функции по p – уравнение, корни которого при заданной температуре дают искомую зависимость p(T),

f(p,T) := ln 11 +− pp + 2zkωT p

Минимизация свободной энергии

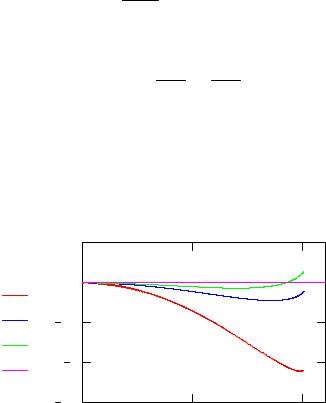
Рассчитаем теперь зависимость параметра дальнего порядка от температуры, минимизируя конфигурационную свободную энергию сплава. График минимизируемой функции для нескольких значений температуры показан на рис. 1. При низких температурах точка экстремума находится около p = 1, а при повышении температуры смещается к нулю.

Для минимизации используем метод золотого сечения [см. 10,11]. Возможный вариант реализации –(см. ниже) функция GoldS(U,a,b,T), аргументы которой U(p,T) – минимизируемая функция, a и b – гра-

74

ницы интервала, на котором ищется мининум, T– температура. При выборе интервала поиска минимума для разных температур будем использовать точку, полученную для предыдущей температуры.

c← a + ξ (b − a)

d← b − ξ (b − a) Uc ← U(c,T)

Ud ← U(d,T)

while b − a > TOL if Uc < Ud

a ← d d ← c

c ← a + ξ (b − a) Ud ← Uc

Uc ← U(c,T)

otherwise b ← c

c ← d

d ← b − ξ (b − a) Uc ← Ud

Ud ← U(d,T) rm ← a +2 b

Наряду с методом золотого сечения воспользуемся встроенной функцией Minimize(), переопределяя с ее помощью функцию пользователя pm(p,T) для использования при разных температурах. Пусть

i := 1 .. I Ti := i Tβ I− 1 pgsi := gs(pgsi−1,Ti) pmTi := pm(pmTi−1,Ti)

75

Упражнения

1. Рассчитайте зависимость параметра порядка от температуры для сплава стехиометрического состава, решая каким-либо численным методом трансцендентное уравнение

2.Постройте график поверхности свободной энергии как функции параметра порядка p и температуры T при фиксированной концентрации одного из элементов сплава с составом, отличным от стехиометрического. Как зависят от этой концентрации максимальные значения параметра порядка и температура перехода?

3.Рассчитайте температурную зависимость параметра порядка для сплава с составом Ca = 0.25; Ca = 0.3; Ca = 0.4 и решеткой ОЦК, минимизируя выражение для свободной энергии методом золотого сечения или используя встроенную функцию Minimize().

4.Рассчитайте зависимость параметра порядка от температуры для сплава нестехиометрического состава, решая уравнение

5. Предположим, что бинарный сплав Cu-Zn содержит примесь атомов типа С малой концентрации. В этом приближении (см. [18]) условие равновесия имеет вид

Считая энергии v и ωпримерно равными, найдите зависимость параметра порядка от температуры и покажите, что температура фазового перехода в тройном сплаве выше, чем в бинарном.

6. Условие равновесия в приближении Кирквуда(см.[18]) имеет вид

Для сплава Cu-Zn стехиометрического состава сопоставьте Ваши результаты с приближением Брегга-Вильямса и экспериментом для параметра порядка и теплоемкости в зависимости от T/Tc.

7. Рассчитайте зависимость параметра p от температуры для сплава Cu3Au стехиометрического состава (см. [18], с. 209). Покажите, что в этом случае имеет место фазовый переход первого рода (Tc = 665K).

77

Глава 9. Параметры кристаллов инертных газов

(решение систем нелинейных уравнений)

Используя экспериментальные данные о характеристиках кристаллов инертных газов найдем оптимальные значения для выбранной параметризации потенциала взаимодействия атомов.

Равновесные характеристики кристалла

При анализе свойств инертных газов [13,14] хорошим приближением является описание взаимного притяжения атомов из-за действия ван- дер-вальсовских сил на основе потенциала Ленарда-Джонса (6-12)

где r – взаимное расстояние между атомами, а параметры ε и σ определяют глубину потенциальной ямы и координату минимума

для 6-12 – потенциала

rmin = σ 6 2

Обычно численные значения дляσ и ε выбирают (см. [14]) на основе анализа взаимодействия атомов в газовой фазе и затем оценивают параметры кристаллов. Поскольку закон взаимодействия на малых расстояниях однозначно не установлен, то зависимость Uo(r) ≈ r -12

часто выбирают для облегчения численных расчетов.

Рассмотрим обратную задачу о поиске параметров потенциала взаимодействия атомов для лучшего согласия с экспериментальными данными о параметрах кристалла. Равновесное положение атомов в кристалле должно соответствовать минимуму удельной энергии.

Пусть R – расстояние между соседними атомами. Выполним суммирование энергии парных взаимодействий в ГЦК– решетке кристалла и получим выражение для удельной энергии

где C6 и C12 - решеточные суммы для ГЦК -решетки (см. [13-15]). Условие минимума удельной энергии – обращение в ноль производной по R приводит к следующей зависимостиσ и R

78

Тогда удельная энергия представляется в виде линейной функции

а модуль всесторонннего сжатия (1010 dyn/cm2/at) имеет вид

Система нелинейных уравнений

Пусть Rex, Uex и Bex – экспериментально наблюдаемые значения для равновесного расстояния между атомами, удельной энергии кристалла и модуля всестороннего сжатия. Введем целевую функцию, характеризующую относительную погрешность сопоставления расчетных и экспериментальных значений. Из условия минимума этой функции будем искать параметры σ и ε потенциала взаимодействия атомов в условиях плотной упаковки в кристалле.

Необходимые условия минимума определяют систему из двух нелинейных уравнений для нахождения неизвестных σ и ε

79