
Karmanov_Trojanov
.pdf
Проверка точности нахождения собственных векторов – расчет невязки системы уравнений:
|
0.992 |
−0.124 |
−0.011 |
0.035 |
|
|
|
|
|
|
||
|
|
0.124 |
0.936 |
0.313 |
−0.101 |
|
|
|
|
|
|
|
C = |
|
|
|
|
|
|
|
|||||
|
−0.016 |
−0.325 |
0.836 |
−0.441 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||||
|
−0.032 |
−0.049 |
0.45 |
0.891 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
||
j := 0 .. 3 δC j := H C j − G C j |
|
|
|
0 0 0 |
0 |
|||||||
δC = |
|
|||||||||||
|
|
|
j |
|
|
|
|
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
||
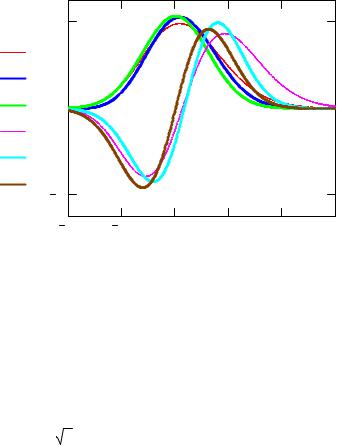
Волновые функции первых состояний
Рассчитанные пробные функции (штриховые кривые), точные волновые функции (сплошные линии) и волновые функции основного и первого возбужденного состояний гармонического осциллятора (пунктир) показаны на рис. 2.
ro := 0.74166 |
A |
|
γ := |
2 ro |
2 mc2 Vo |
||
|
|
||||||
β(n) := |
ro |
|
−2 mc2 Eth |
|
y(x) :=α hcexp(−α x) γ |
||
|
n |
||||||
|
α hc |
|
|
|
|
||
|
|
|
|
|
|
||
Точная волновая функция и ее нормировка:
ψ(n,x) := exp −y(x) y(x)β(n) mhyper(−n,2 β(n) + 1,y(x))
2
⌠1 |
A12(n) := if (n > 1,−1,1) |
A12(n) := ψ(n,x)2 dx |
|
⌡− 1 |
A12(n) |
|
3 |
ψ(n,x) := A12(n) ψ(n,x) |
Φ(n,x) := ∑ Cj,n U(x) j |
|
j = 0 |
40
|
2 |
|
|
|
|
ψ(0,x) |
|
|
|
|
|
Φ(0,x) |
|
|
|
|
|
u0(x) |
|
|
|
|
|
ψ(1,x) |
0 |
|
|
|
|
|
|
|
|
|
|
Φ(1,x) |
|
|
|
|
|
u1(x) |
|
|
|
|
|
|
2 |
|
|
|
|
|
0.4 |
0.2 |
0 |
0.2 |
0.4 |
|
|
|
|
x |
|
|
Рис. 2. Волновые функции первых состояний |
||||
Упражнения
1.Оцените влияние левой границы интегрирования по области локализации волновых функций гармонического осциллятора на значения рассчитываемых матричных элементов потенциала V(x).
2.Используя табличный интеграл (Re(p)>0)
|
⌠∞ |
(a x2 + b x + c)exp(−p x2 − q x)dx |
|
||||||||||||
|
I = |
|
|
||||||||||||
|
⌡− ∞ |
|
|
|
|
|
|
|
|
2 |
|
||||
|
π |
|
|
|
|
|
|
|
( |
|
+ ) |
|
|||
I = |
|
|
|
2 |
− |
+ |
|
2 |
|
|
q |
|
|||
2.5 |
|
a |
q |
|
|
||||||||||
|
|
4 c p |
4 p q b |
|
|
2 p |
|
exp 4 p |
|||||||
|
4 p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
проверьте правильность вычисления матричных элементов H и W. 3. На основании теоремы Гершгорина дайте оценку локализации собственных значений матрицы H (см. [10]).
4. Предполагая известными значения матричных элементов гамильтониана, получите характеристическое уравнение в виде полинома 4 –го порядка относительно переменной E и найдите корни этого полинома, используя встроенную функцию polyroots().
5. Рассчитайте собственные значения гамильтониана H как корни
характеристического или векового уравнения
41

D(E) = H − E I = 0 ,
где I – единичная матрица 4-го порядка. Проведите графический анализ расположения корней и вычислите корни, используя встроенную функцию root().
6. Используя встроенную функцию lsolve(), найдите собственные векторы C из решения системы уравнений
3 |
(Hj,k − E δj,k)cj = 0 , |
|
∑ |
k = 0 .. 3 . |
j = 0
7. Считая известными собственные значения энергии, найдите собственные векторы матрицы H, используя метод квадратного корня (разложение Холецкого). Для выполнения разложения Холецкого можно воспользоваться встроенной функцией cholesky().
8.Рассчитайте собственные значения и собственные векторы для гамильтониана данной задачи итерационным методом, используя QR - разложение.
9.Проверьте нормировку и ортогональность рассчитанных волновых функций.
10.Используя точную волновую функцию Ψ(x)n для молекулы H2 в потенциале Морса, рассчитайте матричные элементы гамильтониана для первых четырех состояний. Дайте оценку обусловленности задачи вычисления собственных значений и собственных векторов гамильтониана H (см. [10]).
11.Согласно теореме вириала для гармонического осциллятора, среднее значение кинетической энергии в каждом состоянии равно среднему значению потенциальной энергии в этом же состоянии. Проверьте, выполняется ли эта теорема для состояний с рассчитанными волновыми функциями.
12.Используя линейный вариационный метод Ритца и волновые функции гармонического осциллятора, рассчитайте уровни энергии
первых 4-х состояний молекулы H2 в потенциале вида (см. [9])
a) |
V(x) = −Vo |
|
|
|
2 |
2 |
|
3 |
3 |
|
7 |
|
4 |
4 |
, |
|
1 |
− α |
|
x |
+ α |
|
x |
− |
|
α |
|
x |
|||
|
|
12 |
|
b) в потенциале Кратцера с параметрами, указанными выше, V(r) = −Vo ror 2 − ror .
42
Глава 4. Равновесное положение атомов ионного кристалла NaCl
(решение нелинейных уравнений)
Рассчитаем равновесное положение атомов и удельную энергию связи ионного кристалла NaCl.
Потенциал взаимодействия
Будем считать, что потенциал взаимодействия пары ионов решетки кристалла может быть представлен как сумма кулоновского потенциала и центрального потенциала отталкивания, записанного в форме БорнаМайера [13] :
|
|
−r |
, j |
|
|
q q |
j |
|
||
U |
= λ exp |
i |
|
+ |
i |
, |
||||
ρ |
|
|
|
r |
|
|
||||
i, j |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
i, j |
|
||
где λ и ρ − эмпирические параметры потенциала Борна-Майера, ri,j – расстояние между ионами и qi , qj – их заряды.
Поскольку взаимное отталкивание является короткодействующим, то его вклад при суммировании достаточно учесть только для ближайших (соседних) атомов и тогда полная энергия кристалла представляется в виде
|
|
|
|
|
|
−R |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Utot(R) = |
N z λ exp |
+ |
|
q |
|
α |
|
|
, |
|
|
|
|
|
||||||
|
|
|
|
ρ |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
R |
|
|
|
|
|
|
|
|
|
|||||||
где N = 1, z = 6 – число ближайших соседей |
(координационное |
||||||||||||||||||||||
число), q2 = 14.409 eV*A, |
α = –1.747565 – постоянная Маделунга |
||||||||||||||||||||||
для решетки NaCl; λ = 1.094 keV, |
|
ρ = 0.321 A |
– значения пара- |
||||||||||||||||||||
метров потенциала, R –расстояние между ближайшими соседями. |
|||||||||||||||||||||||
Равновесное положение ионов в решетке отвечает условию |
|||||||||||||||||||||||
|
d |
|
Utot(R) = 0 |
или |
|
R |
2 |
exp |
−R |
= |
|
|
α |
|
|
q2 ρ |
. |
||||||
|
|
|
|
|
|||||||||||||||||||
dR |
|
|
|
ρ |
|
|
|
z λ |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
43
|
Отделение корней |
|
|
||||||
Задаем константы и определяем полную энергию решетки: |
|||||||||
z := 6 |
q2 := 14.409 |
α := −1.747565 |
λ := 1.094 103 |
||||||
ρ := 0.321 |
Utot(R) := |
z λ exp |
|
−R |
+ |
q2 |
α |
R := 1.0,1.01 .. 6 |
|
|
ρ |
R |
|||||||
|
|
|
|
|
|
||||
|
10 |
|
|
|
|
|
|
|
|
Utot(R) |
|
|
|
|
|
|
|
||
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
10 1 |
2 |
|
3 |
|
4 |
5 |
||
|
|
|
|
R |
|
|
|
|
|
|
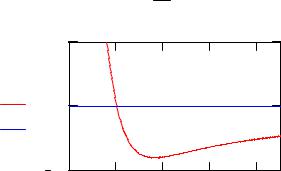
Рис. 1. Удельная энергия кристалла |
||||||||
Используя режим Format-> Graph-> Trace получаем оценку равновесного положения и удельной энергии кристалла:
Rmn = 2.84 A , |
Umn = −7.9228 eV . |
Уравнение, определяющее равновесное положение кристалла,
f(R) := R |
2 |
exp |
−R |
+ |
α q2 ρ |
|
|
|
ρ |
z λ |
|||
|
|
|
|
|||
Метод половинного деления
Алгоритм метода половинного деления [11] реализован в виде подпрограммы Rmin(f,a,b), представленной ниже. Параметры этой подпрограммы: f – функция, задающая уравнение; a и b – начальные границы интервала, на котором ищется корень. Программа проверяет наличие одного действительного корня на заданном отрезке. Если корней нет или их четное число на данном отрезке, то программа выдает сообщение "No Root". Точность расчета корня eps
характеризуется шириной интервала локализации корня.
44
Answer := "No Root" |
|
|
Rmin(f,a,b) := eps ← 0.001 |
|
|
fa ← f(a) |
|
|
fb ← f(b) |
|
|
return |
Answer |
if fa fb > 0 |
while |
b − a |
> 2eps |
c ← a +2 b fc ← f(c)
b ← c if fa fc < 0
otherwise a ← c
fa ← fc rm ← a +2 b
Поскольку в данном случае корень находится на интервале [2,3], то, используя подпрограмму Rmin, можно вычислить корень урав-
нения f(R) = 0. Используя пункт меню Format-> Result-> Number Format-> Number of decimal places, установим режим представления результатов, например, с 5-ю десятичными знаками после запятой, для того, чтобы можно было следить за динамикой изменения погрешности разных методов при выбранном уровне точности eps = 0.001.
Rmin(f,2,3) = 2.81543
Оценка невязки для уравнения f(R) = 0 :
f(RmRm:=) =Rmin(f,2,3) f(Rm) = −1.21358 × 10− 6
а, например, для интервала [3,5] получаем ответ, свидетельствующий об отсутствии корня:
Rmin(f,3,5) = "No Root"
Итак : |
Rm = 2.81543 |
Utot(Rm) = −7.92509 |
45
Метод Ньютона
Метод Ньютона [11] реализован в виде подпрограммы– функции newton (f,df,Rold,eps). Параметры этой подпрограммы:
f – функция, представляющая уравнение, df – функция, задающая производную функции f, Rold – начальное приближение к корню и eps – точность вычисления корня.
newton(f,df ,Rold,eps) := |
Rnew ← Rold − |
|
f(Rold) |
|
|||||||||||
df (Rold) |
|||||||||||||||
|
|
|
|
|
|
||||||||||
|
|
while |
|
Rnew − Rold |
|
|
> eps |
||||||||
|
|
|
|
||||||||||||
|
|
|
Rold ← Rnew |
|
|
|
f(Rold) |
|
|||||||
|
|
|
|
|
|
||||||||||
|
|
|
Rnew ← Rold |
− |
|
|
|||||||||
|
|
|
df (Rold) |
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
Rnew |
|
|
|
|
|
|
|
|
|||||
Производную определяем аналитически: |
df (R) := |
d |
f(R) |
||||||||||||
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
dR |
||||
и находим корень: |
newton(f,df ,2.0,0.001) = 2.81502 |
||||||||||||||
или |
Rn := newton(f,df ,2.0,0.001) |
|
|
|
Rn = 2.81502 |
||||||||||
Интересно отметить, что, несмотря на одинаковые требования к точности вычисления корней (eps = 0.001) в методе половинного деления и методе Ньютона, невязка уравнения f(R) = 0 в данном случае много меньше.
f(newton(f,df ,2.0,0.001)) = 8.19403 × 10− 10
или f(Rn) = 8.19403 × 10− 10
Определение корней с помощью функции root(y,x)
Прежде всего, проверим используемое по умолчанию значение параметра TOL , определяющего "точность" вычисления корня,
|
TOL = 1 × 10− 3 |
|
|
Задаем начальное приближение |
r := 2 |
и вычисляем корень. |
|
rmin := root(f(r) ,r) |
rmin = 2.57618 |
f(rmin) = 9.38923 × 10− 4 |
|
46
Ясно, что требуемая точность вычисления корня не достигается и параметр TOL задает ограничение на точность, с которой выражение f(r) может считаться равным нулю!!!
Переопределяем параметр |
TOL := 10− 7 |
и пробуем снова: |
||
rmin := root(f(r) ,r) |
rmin = 2.81502 |
f(rmin) = 3.31958 × 10− 10 |
||
Теперь результаты расчета корней тремя способами совпадают!
Итерационный процесс
Проследим за динамикой изменения положения корня и невязки в ходе итерационного процесса. Для этого модифицируем программу вычисления корня по методу Ньютона и построим графическую иллюстрацию к итерационному процессу.
Newton(f,df ,Rold,eps) := |
j ← 0 |
|
|
|
|
|
|
|
||||
|
zj,0 ← Rold |
|
|
|
|
|||||||
|
zj,1 ← f(Rold) |
|
|
|
|
|||||||
|
Rnew |
← Rold − |
f(Rold) |
|
||||||||
df (Rold) |
||||||||||||
|
|
|
|
|
|
|
||||||
|
while |
|
Rnew − Rold |
|
|
> eps |
||||||
|
|
|||||||||||
|
|
|
|
zj+1,0 ← Rnew |
|
|
|
|
||||
|
|
|
|
|
|
|
||||||
|
|
|
|
zj+1,1 ← 0 |
|
|
|
|
||||
|
|
|
|
j ← j + 2 |
|
|
|
|
||||
|
|
|
|
zj,0 ← Rnew |
|
|
|
|
||||
|
|
|
|
zj,1 ← f(Rnew) |
|
|
|
|
||||
|
|
|
|
Rold ← Rnew |
|
|
|
|
||||
|
|
|
|
Rnew ← Rold − |
|
|
f(Rold) |
|||||
|
df (Rold) |
|||||||||||
|
|
|
|
|
|
|
|
|
||||
|
z |
|
|
|
|
|
|
|
||||
47
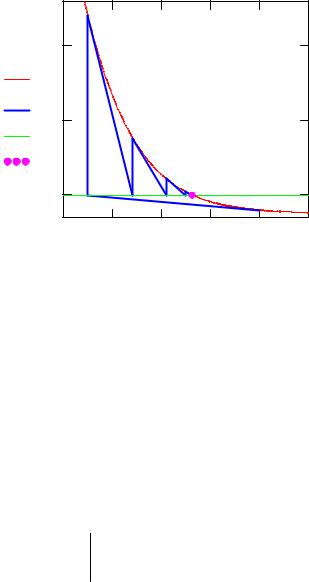
XF := |
Newton(f,df ,3.5,10− 3) |
J := |
rows(XF) − 1 |
|
|||
|
0.01 |
|
|
|
|
|
|
f(x) |
|
|
|
|
|
|
|
XF 1 |
|
|
|
|
|
|
|
0 |
0.005 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
1.5 |
2 |
2.5 |
3 |
3.5 |
4 |
|
|
|
|
x,XF 0 ,x,(XF 0 ) |
J |
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 2. |
Динамика итерационного процесса |
|
|||
Упражнения
1.Рассчитайте постоянную Маделунга кристалла NaCl (см. [13–15]).
2.Выполните суммирование энергий взаимодействия пар ионов по решетке NaCl и получите выражение Utot(R) для удельной энер-
гии кристалла (см. [13–15]).
3. Постройте графическую иллюстрацию итерационного процесса нахождения корня методом половинного деления. Оцените скорость сходимости.
4. На основе вычислительного эксперимента оцените границы области сходимости метода Ньютона в данной задаче. Сопоставьте Ваши результаты с достаточным условием
|
d2 |
|
|
|
d |
|
2 |
|
|
|
|
|
|||||
f(x) |
|
|
f(x) |
< |
|
|
f(x) |
|
dx2 |
|
|
|
|||||
|
|
|
|
dx |
|
|||
|
|
|
|
|
|
|
|
|
48

5. В данной задаче на основе вычислительного эксперимента оцените границы области монотоннойсходимости метода Ньютона и скорость его сходимости.
6.Напишите программу и найдите методом секущих ([10–12]) равновесные параметры кристалла NaCl. Постройте графическую иллюстрацию итерационного процесса.
7.На основе вычислительного эксперимента оцените границы области сходимости, скорость сходимости метода секущих в данной задаче. Сопоставьте Ваши результаты с результатами упражнений 4–5.
8.Предполагая, что атомы инертных газов взаимодействуют между собой посредством потенциала Ленарда-Джонса [13–15],
|
σ |
12 |
− |
σ |
6 |
, |
U(r) = 4 ε |
|
|
r |
|
||
r |
|
|
|
|
||
получите выражение для удельной энергии кристалла с гранецентрированной (ГЦК) решеткой
|
1 |
|
|
|
σ |
12 |
|
|
σ |
6 |
Utot(R) = |
(4 ε) C |
12 |
|
|
− C |
6 |
. |
|||
|
2 |
|
|
R |
|
|
R |
|
Здесь С6 , С12 – решеточные суммы для ГЦК – решетки, а ε и σ – параметры потенциала Ленарда-Джонса.
9. Рассчитайте решеточные суммы С6 , С12 для ГЦК– решетки кристаллов инертных газов (см. [13–15]).
10. Принимая следующие значения параметров потенциала ЛенардаДжонса для атомов Ne
σ = 2.74 А, |
ε = 0.0031 eV, |
рассчитайте любым из методов, обсуждавшихся в данном разделе, равновесное положение, удельную энергию и модуль всестороннего сжатия B для ГЦК решетки кристалла Ne, если
|
2 |
|
2 |
|
|
|
|
|
d |
|
|
. |
|
B = |
|
|
|
|
|
|
9 R |
|
2Utot(R) |
||||
|
|
dR |
|
|
R=Ro |
|
49
