
Karmanov_Trojanov
.pdfПреобразуем найденные выше границы интервалов в границы зон по энергии с помощью функции
EgrZone(E1,E_1,N) := |
for n 0 .. N − 1 |
|||
|
|
if |
(mod(n,2) = 0) |
|
|
|
|||
|
|
|
Egn,0 ← E1n |
|
|
|
|
||
|
|
|
Egn,1 |
← E_1n |
|
|
if |
(mod(n,2) = 1) |
|
|
|
|
Egn,0 |
← E_1n |
|
|
|
||
|
|
|
Egn,1 |
← E1n |
|
Eg |
|
|
|
Для параметров потенциала, соответствующих рис.2, границы зон имеют следующие значения:
|
|
1.313 |
1.655 |
|
Egr := EgrZone(Ea1,Ea_1,Nlev1) |
Egr = |
5.119 |
6.598 |
|
|
|
|
14.767 |
|
|
|
11.09 |
||
Связь квазиимпульса и энергии для расширенной схемы представления зон получим при ss = 1, а для приведенной– при ss = 0. Параметр М позволяет контролировать точность расчета и отслеживать детали дисперсионной кривой в окрестности краев зон.
Q1_imp := Quasi_im(Egr,Nlev1,1,300)
Ee1 := Q1_imp 0 |
Ka1 := Q1_imp 1 |
Fka1 := Q1_imp 2 |
Q0_imp := Quasi_im(Egr,Nlev1,0,300) |
||
Ee0 := Q0_imp 0 |
Ka0 := Q0_imp 1 |
Fka0 := Q0_imp 2 |
Для явного выделения зон области энергий пометим штриховкой
kamax := Nlev1 π |
kgr0 := 0 |
kgr1 := π |
|
J := |
rows(Ka0) − 1 |
J = 902 |
i := 0 .. 1 |
j := |
0,50 .. J |
Yi, j := Ee0j |
|
30
|
15 |
|
|
|
Ee1 |
|
|
|
|
Fka1 |
10 |
|
|
|
|
|
|
|
|
Ee0 |
|
|
|
|
Fka0 |
|
|
|
|
Y |
5 |
|
|
|
|
|
|
|
|
|
0 0 |
3.14 |
6.28 |
9.42 |
|
|
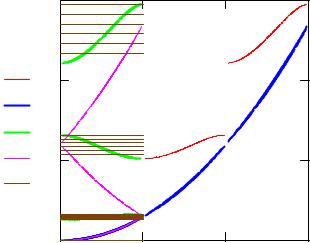
Ka1,Ka1,Ka0,Ka0,kgr |
|
|
Рис. 3. Представление расширенных и приведенных зон для энергии |
||||
электрона как функции волнового вектора в одномерной модели |
||||
Кронига – Пенни. Пунктирной линией показано дисперсионное соот- |
||||
ношение для свободных электронов, а зоны допустимых энергий |
||||
заштрихованы |
|
|
|
|
|
|
Упражнения |
|
|
1.В условиях данной задачи рассчитайте зависимость эффективной массы электрона от энергии в пределах одной зоны (см. [7,13,14]).
2.Для выбранных Вами параметров потенциала рассчитайте уровни энергии в симметричной потенциальной решетке для различных
значений N0 –числа атомов в решетке (см. глава 1) и границы зон по энергии согласно модели Кронига-Пенни. Как согласуются гра-
ницы областей энергии, в которых расположены группы уровней, с результатами модели Кронига-Пенни при увеличении количества атомов в решетке?
3. Покажите, что если перейти от потенциала, представленного на рис.1, к цепочке, состоящей из очень большого числа δ - функций, в предположении, что b –> 0 и V0 –> ∞ , но bV0 = const, то в этом
предельном переходе величина
31

m V
0 a b = γ ,
h2
пропорциональная площади внутри барьера, остается постоянной, а уравнение для определения энергетических зон принимает вид
γ sin(α a) + cos(α a) = cos(k a) .
αa
4.Используя результат упр.3, рассчитайте зонную структуру, дисперсионную кривую и зависимость эффективной массы электрона от энергии или импульса для дираковской потенциальной гребенки
V(x) = α ∑δ(x − n a) .
n
5.Рассмотрим дираковскую потенциальную гребенку с дефектом
-вакансией в точке x = 0
V(x) = α ∑δ(x − n a) , |
n ≠ 0 . |
n
Известно (см. [8]), что в данной задаче, как и в задаче для строго периодического потенциала, разрешенные зоны энергий остаются допустимыми, но появляются дополнительные уровни, обусловленные дефектом в решетке. Покажите, что волновые функции этих состояний могут быть только четными, а нечетных состояний нет. Найдите уровни энергии и нормированные волновые функции нескольких нижних состояний. При α > 0 проанализируйте взаимное расположение зон и этих уровней.
6. Пусть распределение потенциала в системе имеет вид дираковской потенциальной гребенки при x > 0 и ступенки высоты U0 при x < 0
V(x) = α ∑δ(x − n a) , |
n > 0 . |
n
Такое распределение потенциала можно рассматривать как модельное при анализе поверхностных (таммовских) состояний – дополнительных уровней, локализованных вблизи поверхности, расположенной при x = 0. Рассчитайте уровни энергии и нормированные волновые функции нескольких нижних состояний. При α > 0 проанализируйте взаимное расположение зон и этих уровней (см. [8]).
32
7. Используя матричный метод (см. глава 1) и введенные выше обозначения для волновых чисел α(e) и β(e), постройте матрицу перехода для одного периода системы в задаче Кронига - Пенни:
T(e) = Dαβ(e) Pα(e) Dβα(e) Pβ(e) .
Убедитесь в том, что определитель этой матрицы равен единице, а половина ее следа определяется суммой функций f1(e) и f2(e):
0.5 tr(T(e)) = f1(e) + f2(e) .
8. Покажите, что условием существования периодического (ограниченного и незатухающего) решения в системе является равенство единице модуля собственных значений матрицы перехода T(e), а условия, определяющие границы зон по энергии, имеют вид:
−1 ≤ 0.5 tr(T(e)) ≤ 1 .
9. Предположим, что одномерная модельаморфного твердого тела представляет собой цепочку одинаковых потенциальных ям, разделенных барьерами переменной ширины. Задавая период системы согласно какому-либо правилу (или распределению случайных величин со средним значением, близким к периоду однородной цепочки атомов), получите условия, определяющие зонную структуру спектра, и сопоставьте ее с зонной структурой однородной цепочки атомов. Как изменяются результаты при увеличении степени беспорядка в системе? При каких условиях возможно исчезновение запрещенных зон при высоких энергиях?
10. Предположим, что распределение потенциала в одномерной модели сверхрешетки, состоящей из чередующихся слоев GaAs (яма) и Al0.5Ga0.5As (барьер) и ограниченной при x < 0 вакуумом, имеет вид потенциальной ступеньки U(x) = U0 при x < 0, U(x) = 0 и V0 в пределах ямы и барьера, соответственно. Полагая период равным a =75A, ширину барьера b = 15A, а потенциалы U0 = 4.0 eV и V0 = 0.4 eV, рассчитайте матричным методом зонную структуру, дисперсионную кривую и зависимость эффективной массы электронов от энергии при 0 < E < V0 < U0 .
11. В условиях упр. 10 рассчитайте уровни энергии и волновые функции нескольких низколежащих поверхностных состояний и найдите такие условия, при которых эти состояния расположены в зоне запрещенных значений энергии бездефектной решетки.
33
Глава 3. Линейный вариационный метод Ритца
(задача на собственные значения для систем линейных уравнений)
Одним из широко используемых методов приближенного решения уравнения Шредингера является вариационный метод. Он основан на утверждении о том, что если минимальное собственное значение гамильтониана H равно E0 , а Ψ – точная волновая функция этого состояния, то для любой нормированной (пробной) волновой функции Ф выполняется условие [1,2,9]: среднее значение энергии в состоянии с функцией Ф
|
⌠ |
Φ• H Φ dτ ≥ |
⌠ |
Ψ• H Ψ dτ = E . |
E = |
|
|
||
|
|
|
|
0 |
|
⌡ |
|
⌡ |
|
Результат расчета вариационным методом критически зависит от выбора пробной функции Ф. Чем лучше пробная функция аппроксимирует точную, тем ближе значение энергии, полученное с помощью этой пробной функции, к истинному значению энергии. Для выбора пробной функции следует принимать во внимание любую дополнительную информацию о решении, например, асимптотическое поведение точной волновой функции в нуле или на бесконечности, свойство четности, положение максимумов или минимумов, возможную близость искомой волновой функции к волновой функции задачи, для которой известно точное решение, и т.д.
Часто задачу о поиске экстремума функционала энергии рассматривают на определенном классе параметрически заданных функций. При этом задача сводится к поиску экстремума энергии как функции многих переменных – параметров пробной волновой функции.
Необходимым условием экстремума является обращение в ноль производных от средней энергии по каждому из параметров пробной функции. В такой постановке процедура минимизации функционала известна как вариационный метод Ритца.
В линейном варианте метода Ритца пробная волновая функция выбирается в виде линейной комбинации независимых функций
n−1 |
|
Φ = ∑ cj φj , |
где сj – варьируемые |
j = 0 |
параметры. |
|
Считая, что Ф ненормирована, а φj и φk неортогональны, подставим Ф в выражение для средней энергии и получим
34

∑∑(c•)j ck Hj,k
|
|
|
|
E = |
|
j |
k |
|
|
|
|
|
|
|
|
|
|
∑∑(c•)j ck Sj,k |
|
|
|
|
|||
|
|
|
|
|
|
j |
k |
|
|
|
|
|
или |
∑∑(c•)j ck Hj,k − |
E ∑∑(c•)j ck Sj,k = 0 , |
||||||||||
|
j |
k |
|
|
|
|
|
j k |
|
|
|
|
|
|
|
⌠ |
(φ•) |
|
|
|
|
|
⌠ |
(φ•)φ |
|
где |
Hj,k |
= |
|
|
φ |
τ, |
Sj,k = |
|
τ |
|||
|
|
|
j H |
k d |
|
j |
k d |
|||||
|
|
|
⌡ |
|
|
|
|
|
|
⌡ |
|
|
– матричные элементы гамильтониана H и интегралов перекрывания функций φj .
Здесь энергия является квадратичным функционалом относительно вектора параметров С. Дифференцируя по c^j и принимая во внимание тот факт, что производная средней энергии по этому параметру должна обращаться в ноль, находим
n−1
∑ ck (Hj,k − E Sj,k)= 0 . k = 0
Полученная система линейных однородных уравнений имеет нетривиальное решение только тогда, когда ее детерминант D(E) = 0. Соотношение
Hj,k − E Sj,k = 0
называется характеристическимили вековым уравнением и из его решения находят n корней. Минимальное значение из корней соответствует энергии основного состояния, а остальные – энергии возбужденных состояний.
Полное решение задачи о собственных значениях – определение корней векового уравнения и нахождение параметров ck – позволяет найти волновые функции основного и возбужденных состояний, причем точность описания обычно падает с ростом номера возбужденного состояния.
35
Колебательные состояния молекулы H2 в потенциале Морса
Колебательное движение атомов в двухатомных молекулах сравнительно хорошо описывается потенциалом Морса
V(x) = Vo (exp(−2 α x) − 2 exp(−α x)),
для которого известно точное аналитическое решение [9], позволяющее оценить степень точности вариационного расчета:
|
|
1 |
− |
|
α h |
(n |
|
|
|
2 |
|
||
Eth = −Vo |
|
|
|
+ 0.5) |
, |
|
|||||||
n |
|
|
|
|
2m Vo |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
||||||
Ψ(x)n = A exp |
−y(x) |
|
y(x) |
β(n) |
F |
(−n,2b(n) + 1,y(x)) , |
|||||||
2 |
|
|
|
||||||||||
|
|
|
|
|
|
11 |
|
2 r0 |
|
|
|
||
y(x) = γ exp(−α x) |
, |
|
|
|
|
|
γ = |
|
2 µ V |
, |
|||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
α h |
0 |
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
β(n) = |
|
r0 |
|
−2 µ En . |
|
|
||||||
|
|
|
|
|
|||||||||
|
|
|
|
α h |
|
|
|
|
|
|
|
||
Здесь F11(.,.,.) – вырожденная гипергеометрическая функция, α и V0–
параметры потенциала, A- нормировочная постоянная, r0– равновесное положение атомов в молекуле, µ – приведенная масса ядер и n = 0,1,2,3 ... – номер состояния системы.
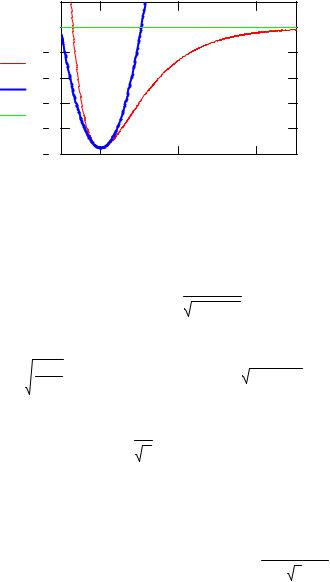
Потенциал и пробная функция для молекулы H2
В окрестности положения равновесия потенциал Морса может быть аппроксимирован потенциалом гармонического осциллятора. Решения уравнения Шредингера для гармонического осциллятора известны в аналитической форме и потому выбор пробной функции для вариационного расчета в виде линейной комбинации нормированных волновых функций нескольких первых состояний может быть хорошим приближением, обеспечивающим правильное асимптотическое поведение при x –> ∞ и x –> –1 , по крайней мере, для основ-
ного и первого возбужденного состояний. Примем следующие параметры для молекулы и определим потенциал взаимодействия атомов:
α := 1.942 Vo := 4.747 eV |
mc2 := 0.5 938.28 106 |
eV |
||||||
hc := 1.9732858 10 |
3 |
eV A |
|
1 |
− |
( |
|
)2 |
|
Uo(x) := −Vo |
|
α x |
|||||
36
|
|
V(x) := Vo (exp(−2 α x) − 2 exp(−α x)) |
||
|
1 |
|
|
|
|
0 |
|
|
|
V(x) |
1 |
|
|
|
|
|
|
|
|
Uo(x) |
2 |
|
|
|
|
|
|
|
|
0 |
3 |
|
|
|
|
4 |
|
|
|
|
5 |
0 |
1 |
2 |
|
|
|||
|
|
|
x |
|
Рис. 1. |
Потенциал Морса и гармонического осциллятора |
|||
Точное решение в потенциале Морса для первых четырех состояний и экспериментальное значение энергии основного состояния:
n := 0 .. 3 |
|
|
1 |
− |
α hc |
2 |
|||
Eth := −Vo |
|
|
|
(n + 0.5) |
|||||
|
|
n |
|
|
|
2mc2 Vo |
|
||
|
|
|
|
|
|||||
|
Eth0 = −4.478 |
eV |
|
Eexp := −4.474 eV |
|||||
ω = α |
2 Vo |
λ = |
m ω |
|
|
λ := |
α |
|
2 mc2 Vo |
m |
h |
|
|
|
|||||
|
|
|
|
|
hc |
|
|||
Область локализации волновых функций по x |
|||||||||
λ = 65.68 |
xo(λ) := 1 |
|
|
xo(λ) = 0.123 |
|||||
|
|
|
λ |
|
|
|
|
|
|
Нормированные волновые функции первых четырех состояний гармонического осциллятора и их вторые производные по x:
|
1 |
|
|
|
|
|
(1 |
− 2 λ x2) |
λ 4 |
|
|
x2 |
|
||||
u0(x) := |
exp |
−λ |
|
|
u2(x) := u0(x) |
|
|
|
|
|
|
||||||
π |
|
|
2 |
|
|
2 |
||
37

u1(x) := u0(x) x 2λ |
|
|
|
u3(x) := u0(x) |
λ x (3 − 2 λ x2) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
du0(x) := |
d |
u0(x) |
|
|
|
|
|
du2(x) := |
|
d |
u2(x) |
|||
2 |
|
|
|
|
|
|
2 |
|||||||
|
dx |
|
|
|
|
|
|
|
|
|
|
dx |
||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
du1(x) := |
d |
u1(x) |
|
|
|
|
|
du3(x) := |
|
d |
u3(x) |
|||
2 |
|
|
|
|
|
|
2 |
|||||||
|
dx |
|
|
|
|
|
|
|
|
|
|
dx |
||
Пробная волновая функция молекулы водорода |
||||||||||||||
Φ(x) = c0 u0(x) + c1 u1(x) + c2 u2(x) + c3 u3(x) |
||||||||||||||
|
H Φ(x) = −h2 |
|
d2 |
Φ(x) + V(x) Φ(x) |
||||||||||
|
|
|||||||||||||
|
|
2 m |
|
dx2 |
|
|
|
|
|
|
|
|
|
|
Среднее значение энергии и минимизируемая функция |
||||||||||||||
|
|
E(c0,c1,c2,c3) = |
(Φ |
|
H |
|
Φ) |
|
|
|||||
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||
|
(Φ |
,Φ) |
|
|
||||||||||
F(c0,c1,c2,c3,ε) = E(co,c1,c2,c3) − ε (Φ,Φ)
Условие экстремума для квадратичного функционала– система линейных уравнений. S – единичная матрица.
3
∑ cj (Hj,k − ε Sj,k)= 0 j = 0
Матричные элементы
Вычисление матричных элементов гамильтониана:
u0(x)
u1(x) U(x) :=
u2(x)u3(x)
|
|
du0(x) |
||
|
d2U(x) := |
du1(x) |
|
|
|
|
|
||
|
||||
|
|
du2(x) |
|
|
|
|
du3(x) |
||
38
|
|
|
|
|
|
|
|
|
|
−hc2 |
⌠∞ |
|
|
|
|
|
|
|
|
j := 0 .. 3 |
k := 0 .. 3 |
Z |
j,k |
:= |
|
|
|
U(x) d2U(x) |
k |
dx |
|||||||||
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
2 mc2 |
⌡ |
|
|
j |
|
|
|
||||
|
|
⌠ |
∞ |
|
|
|
|
|
|
|
|
− ∞ |
|
|
|
|
|
|
|
W |
|
|
|
|
dx |
|
|
|
H |
|
:= Z |
|
+ W |
|
|||||
j,k |
:= |
U(x) V(x) U(x) |
k |
|
|
|
j,k |
j,k |
j,k |
||||||||||
|
⌡ |
|
j |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
− 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
−4.467 |
−0.072 |
|
−0.02 |
0.061 |
|
|
|
|
|||||||
|
|
|
H = |
−0.072 |
−3.894 |
0.207 |
|
−0.058 |
|
|
|
|
|||||||
|
|
|
|
0.207 |
−3.291 |
−0.388 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
−0.02 |
|
|
|
|
|
||||||||||
|
|
|
|
0.061 |
−0.058 |
−0.388 |
−2.658 |
|
|
|
|
||||||||
Собственные векторы и собственные значения
Рассчитаем собственные векторы и собственные значения матрицы H, используя встроенные функции eigenvals() и eigenvecs(). Функция eigenvecs() возвращает матрицу, составленную из собственных векторов:
G := eigenvals(H) |
|
−4.478 |
|
||
|
|
−3.953 |
|
||
C := eigenvecs(H) |
G = |
||||
|
−2.457 |
|
|||
|
|
||||
|
|
|
|
||
|
|
−3.423 |
|||
Внимание! Найденные собственные значения и, конечно, собственные векторы для нашей задачи неправильно упорядочены! Нужно выполнить упорядочивание собственных значений и векторов, переставив 3-й и 4-й столбцы в матрице собственных векторов. Отметим, что векторы уже нормированы на единицу.
G := sort(G) ca := C 2 C 2 := C 3 C 3 := ca
|
−4.478 |
|
−4.478 |
|
|
− 4 |
|
|||
|
|
|
|
2.41 × 10 |
|
|||||
G = |
−3.953 |
|
Eth = |
−3.964 |
|
G − Eth = |
|
0.011 |
|
|
|
|
|
|
|
0.059 |
|
||||
|
|
|
||||||||
|
−3.423 |
|
|
−3.482 |
|
|
|
|
||
|
−2.457 |
|
−3.031 |
|
|
0.573 |
|
|||
Как и следовало ожидать, полученное решение для уровней энергии– оценка сверху, и точность оценки падает с ростом номера состояния!
39
