Karmanov_Reznichenko

Методические указания

к выполнениюлабораторныхработпо курсу «Вычислительные методыв квантовойфизике» Часть 1

Решение системлинейныхуравнений

Карманов Ф.И., Резниченко Д.А.

Данное методическое пособие предназначено для студентов 4-го курса специальности 070500 «Ядерные реакторы и энергетические установки» и 070900 «Физика металлов» и содержит методические рекомендации к выполнению лабораторных работ по курсу «Вычислительные методы в квантовой физике». В пособии рассматриваются постановки задач, формулируются методы их решения, обсуждаются алгоритмы и приводятся подробные тексты программ моделирования с использованием достаточно широких возможностей интегрированного пакета «MathCAD 11a». Особое внимание уделяется созданию программ как инструментов исследования и выполнению компьютерного моделированияизучаемых явлений.

Первая часть содержит материал, относящийся к одному из традиционных разделов вычислительной математики - решениюсистем линейных уравнений.

2

Решение систем линейных алгебраических уравнений

Задача 1

Частица массы m находится в потенциальной яме конечной глубины Uo. Требуется найти допустимые уровни энергии частицы, решая уравнение Шрёдингера для задачи о стационарных состояниях. Ширина ямы равна a.

Рис. 1. Распределение потенциала

Будем искать решение в виде ψ(х) = Аexp(ikx) + Bexp(-ikx), где неизвестные параметры A и B определяются из условий ограниченности волновой функции и непрерывности волновой функции и ее первой производной на границах, т.е. при x=0 и x=a. Выполнение этих условий приводит к следующей системе линейных алгебраических уравнений:

3

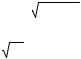
eik1 a A1 + e− ik1 a B1 − eik2 a A2 = 0

k1 ei k1 a A1 − k1 e− ik1 a B1 − k2 eik2 a A2 = 0

Поскольку данная система уравнений однородна, то она однозначно разрешима, только если ее определитель равен нулю, а это и есть необходимое уравнение для определения уровней энергии частицы.

4

( для справок см. Help -> Resource Center -> Quick Sheets, References -> Vectors and Matrices -> Decompositions of Matrices )

Проанализируем структуру полученной матрицы М и извлечем из нее верхнюю U и нижнюю L треугольные матрицы, а также матрицу перестановок Р:

Определитель матрицы С как произведение диагональных элементов

верхней треугольной матрицы, умноженный на (-1)^ p , где р - число перестановок (в нашем случае, судя по найденной матрице Р, была только одна перестановка) и его модуль:

5

Расчет уровней энергии частицы в потенциальной яме

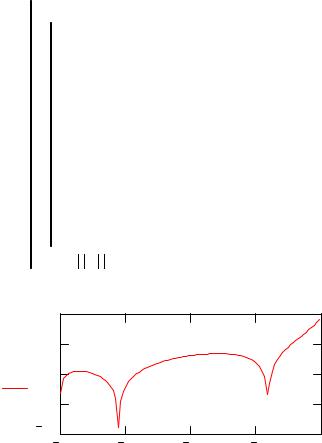
На основе описанного выше алгоритма вычисляем детерминант как функцию энергии с помощью подпрограммы D(E). Поскольку в MathCAD существует встроенная функция вычисления определителя системы линейных уравнений, основанная на использовании разложения матрицы на верхюю и нижнюю треугольную, то воспользуемся этой встроенной функцией.

D(e) := for j 0 .. 2 N − 1

C2 j,2 j−1 ← exp(i k(e, j) Xj) if ( j > 0) C2 j,2j ← exp(−i k(e, j) Xj)

6

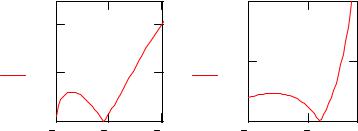
Определение корней с помощью функции root(y,x)

Построим более детальные графики в окрестности предполагаемых значений корней.

Исходя из графика функции D(E) ясно что , приближенные значения корней E1 = -16 , E2 = -4 . Используя встроенную функцию root(f,x), уточняем значения корней:

(для справок см. Help -> Resource Center -> QuickSheets, References -> Solving Equations ->Solving Equations in a Single Unknown)

TOL = 1 × 10− 3 ( значение по умолчанию)

Оценим влияние параметра TOL на точность нахождения корней:

Как видно, требуемая точность нахождения корня (три знака после запятой) достигается при TOL:= 10− 3.Чему равна невязка уравнения?

7

Решение системы линейных уравнений

Поскольку система уравнений однородна, то ее решение может быть найдено только если предположить, что одна из компонент вектора неизвестных может быть определена на основе некоторых дополнительных условий. В нашем случае - это условие нормировки волновой функции. Полагая, например, Bo известной величиной и опуская одно из уравнений исходной системы, получим:

Для нахождения решения этой системы уравнений воспользуемся встроенной функцией lsolve()

(для справок см. Help -> Resource Center -> QuickSheets, References -> Solving Equations ->Solving a Linear System of Equations)

8

Волновые функции состояний

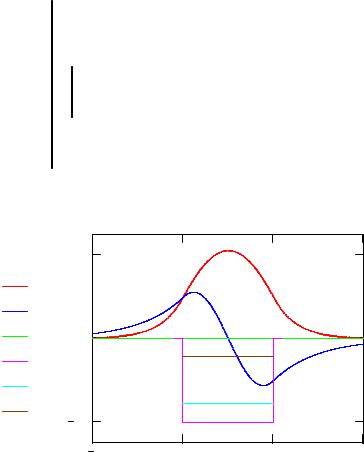
Вычислим теперь значения волновых функций для каждого из найденных состояний и построим их графики. Отметим, что волновые функции являются ненормированными.

ψ(x,e) := ab ← lsolve(M(e) ,V(e))

y ← Bo exp(−i k(e,0) x) if x ≤ 0 if 0 < x < a

y ← ab0 exp(i k(e,1) x)

y ← y + ab1 exp(−i k(e,1) x) y ← ab2 exp(i k(e,0) x) if x ≥ a

y

xx := 0 ..a

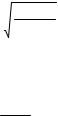
Упражнения

1. Проанализируйте постановку задачи о стационарных состояниях для частицы, находящейся в потенциальной яме конечной глубины (см. [1]). Получите трансцендентное уравнение

где a - ширина ямы, n - номер состояния (целое число), k - волновое число, изменяющееся в диапазоне [0, ko], а ko равно

корни которого определяют значения уровней энергии в таком потенциальном поле. При этом энергия состояния определяется соотношением

2

E = (hk2m) − Uo .

Получите оценку числа стационарных состояний, реализующихся в данной потенциальной яме в зависимости от соотношения ее глубины и ширины

2.Найдите графически решение трансцендентного уравнения, приведенного в упражнении 1, для обсуждавшихся выше параметров потенциала.

3.На основе приведенного выше описания алгоритма «соберите» работающий вариант программы и вычислите значения уровней энергии и волновых функций в потенциальной яме конечной глубины с выбранными Вами параметрами ямы. Проанализируйте результаты на основе информации, приведенной в упражнении 1.

4.Рассчитайте уровни энергии и волновые функции для стационарных состояний частицы в двух близко расположенных потенциальных ямах конечной глубины. Эта система может рассматриваться как простейшая модель ковалентной связи. Какими дополнительными свойствами обладают волновые функции и уровни энергии в этой задаче?

10