
Karmanov_Reznichenko
.pdf
Задача 5
Рассчитать коэффициенты отражения и прохождения частицы через прямоугольный потенциальный барьер.
|
|
|
|
Решение |
|
|
|
|
Аналитический расчет вероятности прохождения |
||||||
Пусть |
a := |
5 |
A |
Uo := 20 eV |
i := −1 |
||
|
mc2 := |
0.511 106 |
eV |
hc := 1.9732858 103 |
eV A |
||
Форму барьера определим следующим образом: |
|
||||||
x := ( −0.5 a |
0 |
0 a a |
1.5 a ) |
u := ( 0.1 |
0.1 Uo |
Uo 0.1 0.1 ) |
|
20
uT
0 |
|
|
|
|
|
|
|
|
|
|
|
5 |
0 |
5 |
10 |
||||
|
|
||||||||
xT
Рис. 1. Потенциальный барьер
Следуя стандартной схеме [1], выписываем решения уравнения Шредингера для трех областей (x<0 , 0<x<a, x>a), принимаем во внимание условия непрерывности волновой функции и ее производной в точках x =0 и x =a и, считая A1 -амплитуду падающей слева на барьер волны равной единице, получаем систему уравнений для определения коэффициентов B1 , A2 , B2 , A3.
Для решения этой системы уравнений воспользуемся специальным вычислительным блоком Given - Find(). Начальные значения в этом случае присваивать не обязательно, а решение получается в символьной форме. Формируем вычислительный блок, определяем список переменных, рассматриваемых как неизвестные, и заканчиваем оператор Find() знаком символьных вычислений (стрелкой) в меню
Evaluation ->, т. е. Find(B1,A2,B2,A3)->
31

Given
1 + B1 = A2 + B2
k1 − k1 B1 = k2 A2 − k2 B2
exp(i k2 a) A2 + exp(−i k2 a) B2 = exp(i k1 a) A3 k2 exp(i k2 a) A2 − k2 exp(−i k2 a) B2 = k1 exp(i k1 a) A3
Find(B1,A2,B2,A3)
Полученное решение очень громоздко и потому здесь полностью не приводится, но его можно упростить, используя символьный процессор. Поскольку нас интересует коэффициент прохождения T = |A3|2, извлечем 4-ю компоненту вектора решения и, собирая в знаменателе дроби подобные слагаемые (Symbolics-> Collect), получаем:
−4 k2 k1 exp(−i k1 a)
A3 =
(k1 − k2)2 exp(i k2 a) − (k1 + k2)2 exp(−i k2 a)
Аналогично, извлекая первую компоненту вектора решения и приводя подобные, находим
B1 = |
(k12 |
− k22)(exp(−i k2 a) − exp(i k2 a)) |
|
|
(k1 − k2)2 exp(i k2 a) − (k1 + k2)2 exp(−i k2 a)
Знаменатель обеих формул можно привести к виду
|
|
i (k12 + k22) |
|
|
|
|
|
|
|
||
−4 k1 k2 |
cos(k2 a) − |
2 k1 k2 |
sin(k2 a) |
и тогда находим точное решение [1] для коэффициента прохождения:
|
|
|
|
2 |
|
2 |
2 |
− 1 |
|
1 |
|
− k1 |
sin(k2 a) |
|
|||
T = |
+ k2 |
|
|
2 |
||||
|
|
|
2 k1 k2 |
|
|
|||
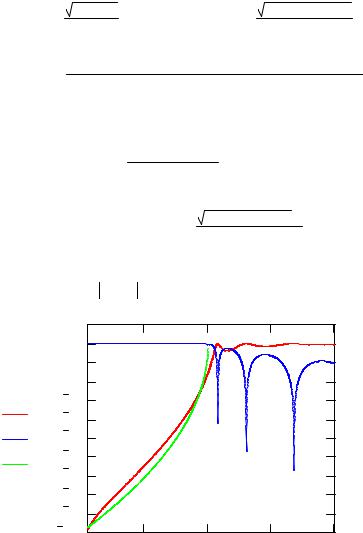
Построим графики зависимости коэффициентов отражения R(E) и прохождения T(E) от энергии E и сравним результат с традиционно используемым [1] приближением Tth(E) для высокого и широкого барьера (a Uo>>1).
32
k1(E) := |
2 mc2 E |
|
|
|
|
k2(E) := |
2 mc2 (E − Uo) |
||||||
|
|
hc |
|
|
|
|
|
|
|
|
|
hc |
|
B1(E) := |
|
(k1(E)2 − k2(E)2)(1 − exp(2 i k2(E) a)) |
|||||||||||
|
(k1(E) − k2(E))2 exp(2 i k2(E) a) − (k1(E) + k2(E))2 |
||||||||||||
|
|
|
|
|
2 |
|
|
|
2 |
|
2 |
− 1 |
|
|
|
|
|
− |
k1(E) |
|
|
||||||
|
T(E) := 1 + |
k2(E) |
|
|
|
sin(k2(E) a)2 |
|||||||
|
|
|
|
2 k1(E) k2(E) |
|
|
|
||||||
|
|
|
|
|
|
|
−2 |
2 mc2 (Uo − E) a |
|
||||
|
Tth(E) := if E |
< Uo,exp |
|
|
|
hc |
|
,0 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R(E) := ( |
B1(E) )2 |
|
|
|
|
|
|
E := |
1,1.01 ..40 |
|||
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
0.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0.01 |
|
|
|
|
|
|
|
|
|
|
|
|
T(E) |
1 .10 3 |
|
|
|
|
|
|
|
|
|
|
|
|
R(E) |
1 .10 4 |
|
|
|
|
|
|
|
|
|
|
|
|
1 .10 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Tth(E) 1 .10 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 .10 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 .10 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 .10 9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 .10 10 |
|
|
10 |
|
|
|
20 |
|
|
30 |
40 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
Рис. 2. |
Коэффициенты отражения и прохождения |
|||||||||||
33
Матричное описание процесса распространения
Волновую функцию частицы в кусочно постоянном потенциале можно представить с помощью двух матриц: вектора-строки плоских волн и вектора-столбца коэффициентов [7]:
ψ(x) = A exp(i k x) + B exp(−i k x) = (ei k x e− i k x ) |
A |
|
B |
При распространении частицы в таком потенциале на расстояние r можно рассматривать две системы координат, для которых
x = x1 + r и ψ1(x1)= ψ(x)
Учитывая это условие, получаем P матрицу распространения:
|
|
|
|
|
i k x |
|
|
|
− i k x |
|
|
|
A e |
i k r |
|
||||
|
ψ(x1 + |
r)= (e |
1 |
e |
1 ) |
|
|
||||||||||||
|
|
|
|
|
|
|
− i k r |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B e |
|
|
||
или |
|
|
|
i k r |
|
|
|
|
|
|
|
|
|
|
|
|
i k r |
|
|
|
A |
|
|
|
0 |
|
|
A |
|
|
A e |
||||||||
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
P |
B |
= |
|
0 e |
− i k r |
|
B |
|
= |
|
|
− i k r |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
B e |
|
|
||||||
|
|
|
|
|
|
i k r |
|
|
|
0 |
|
|
|
|
|
|
|
||
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
P(r) = |
|
0 |
|
|
e |
− i k r |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Пусть потенциал испытывает разрыв в точке x = 0, тогда из условий непрерывности волновой функции и ее производной получаем:
A2 + B2 = A1 + B1 i k2 (A2 − B2)= i k1 (A1 − B1)
Разрешая эту систему уравнений относительно A2 и B2, находим в явном виде матрицу скачка потенциала от U1 (слева) до U2 (справа):
34
|
|
A |
|
|
A |
|
||||||
|
|
|
|
2 |
|
= D |
|
|
1 |
|
||
|
|
B |
2 |
|
12 |
B |
1 |
|
||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
k |
|
|
k |
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
1 + k |
1 − k |
|
|
|
||||||
D = 1 |
|
|
|
|||||||||
|
|
|
2 |
|
|
2 |
|
|
||||
12 |
2 |
|
|
|
k1 |
|
|
k1 |
||||
|
1 − |
1 + |
||||||||||
|
|
|
|
|
|
|
|
|||||
|
|
k |
k |
|
|
|
||||||
|
|
|
|
|
2 |
|
|
2 |
|
|||
В случае δ- потенциала |
вида |
U(x) = α δ(x) система уравнений |
||||||||||
для связи коэффициентов |
волновой функции по обе стороны от |
|||||||||||
барьера будет состоять из условия непрерывности функции и соотношения для скачка производной:
A2 + B2 = A1 + B1
i k (A2 − B2)− i k (A1 − B1)= |
2 m α |
(A1 + B1) |
||||||||||
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
h |
|
|
|
Отсюда получаем матрицу δ- потенциала: |
|
|
||||||||||
|
|
1 |
− |
i m α −i m α |
|
|||||||
Del(α) |
|
k h2 |
k h2 |
|
||||||||
|
|
|
||||||||||
= |
|
|
i m α |
|
i m α |
|
||||||
|
|
|
|
1 + |
|
|||||||
|
|
|
|
2 |
|
|
||||||
|
|
|
|
|
|
2 |
|
|||||
|
|
|
|
k h |
|
k h |
||||||
Отметим, что все волновые числа, входящие в определение матриц, стандартным образом зависят от энергии E и от потенциала U.
Матричный расчет
Воспользуемся введенными матрицами для расчета коэффициента прохождения через прямоугольный барьер следующей формы:
a := 5 |
U3 := 10 |
|
x := ( −0.5 a |
0 0 a a 1.5 a ) |
u := ( 0.1 0.1 Uo Uo U3 U3 ) |
и покажем зависимость результатов от высоты правой ступеньки.
35

20
uT
0 |
|
|
|
|
|
|
|
|
|
|
|
5 |
0 |
5 |
10 |
||||
|
|
||||||||
|
|
|
|
|
|
xT |
|
|
|
Рис. 3. Потенциальный барьер
Вводим матрицы скачков потенциала и распространения волны:
|
|
|
1 |
+ |
k1(E) |
1 |
− |
k1(E) |
|
|
1 |
|
k2(E) |
k2(E) |
|
||||
D12(E) := |
|
|
|
|
|
|
|||
|
2 |
|
1 |
− |
k1(E) |
1 |
+ |
k1(E) |
|
|
|
|
|
|
k2(E) |
|
|
k2(E) |
|
|
k3(E,u3) := |
2 mc2 (E − u3) |
|
|||||||
|
|
hc |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
+ |
k2(E) |
1 − |
k2(E) |
|
||
|
1 |
|
k3(E |
,u3) |
k3(E,u3) |
|
||||
D23(E,u3) := |
|
|
|
|
|
|||||
2 |
|
|
k2(E) |
|
k2(E) |
|||||
|
|
1 |
− |
1 + |
|
|||||
|
|
k3(E,u3) |
k3(E,u3) |
|||||||
|
|
|
|
|
|
|||||
P2(E) := |
exp(i k2(E) a) |
|
0 |
|
|
|||||
|
|
|
0 |
|
exp(−i k2(E) a) |
|||||
|
|
|
|
|
||||||
Пусть каждой из трех областей постоянства потенциала соответствует свой вектор коэффициентов (Aj , Bj ). В рамках обсуждаемого матричного формализма
A |
|
|
A |
|
||
|
3 |
|
= D23(E,u3) P2(E) D12(E) |
|
1 |
|
B |
|
|
B |
|
|
|
|
3 |
|
|
|
1 |
|
36
Использованное здесь произведение матриц определим как матрицу перехода частицы из области с потенциалом U1 = 0 к U3.
T13(E,u3) := D23(E,u3) P2(E) D12(E)
В случае, если волна падает на барьер слева направо, то, как обычно, A1 = 1, B3 = 0 или, если волна падает справа, A1 = 0, B3 = 1 и, в силу симметрии процесса прохождения, система принимает вид
A |
|
1 |
|
A |
|
0 |
|||
|
3 |
= T13(E,u3) |
|
или |
|
3 |
= T13(E,u3) |
|
|
0 |
|
B1 |
|
1 |
|
B1 |
|
||
Отсюда находим: |
B1(E,u3) := (T13(E,u3)1,1)− 1 |
|
|
||||||
|
|
A3(E,u3) := |
T13(E,u3)0,1 B1(E,u3) |
|
|
||||
Вычисляя плотности потоков вероятности (см. [1,8] ), получаем
T(E,u3) := ( |
|
B1(E,u3) |
|
)2 |
|
k1(E) |
|
R(E,u3) := ( |
|
A3(E,u3) |
|
)2 |
||
|
|
|
|
|
|
|||||||||
|
|
k3(E,u3) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
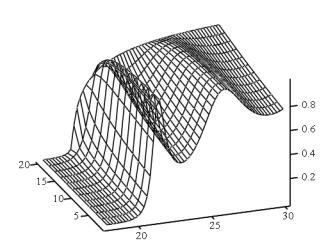
T
Рис. 4. Зависимость коэффициента прохождения от энергии E и высоты правой ступеньки U3
37
|
Два δ- барьера |
|
|
|
|
|
|
||||
Рассчитаем зависимости коэффициентов отражения и прохождения |
|||||||||||
от энергии через два δ-барьера, отстоящих друг от друга на расстоя- |
|||||||||||
ние d. Обозначим через b |
комбинацию параметров барьера и |
|
|||||||||
определяем матрицы: |
|
|
|
|
|
|
|
|
|
|
|
b = m α |
b := 1 |
|
k(E) := |
2 mc2 E |
|
|
d := 5 |
|
|||
h2 |
|
|
|
|
|
|
hc |
|
|
|
|
|
exp(i k(E) d) |
|
|
|
0 |
|
|
|
|
||
P(E) := |
0 |
|
exp(−i k(E) d) |
|
|
||||||
|
|
|
|
|
|||||||
|
|
|
i b |
|
−i b |
|
|
|
|
||
|
1 |
− k(E) |
|
k(E) |
|
E := |
0,0.01 ..30 |
||||
Del(E) := |
i b |
|
|
i b |
|||||||
|
|
1 |
+ |
|
|
|
|
|
|||
|
|
k(E) |
k(E) |
|
|
|
|
||||
|
T12(E) := Del(E) P(E) Del(E) |
|
|
|
|
||||||
T2(E) := ( |
T12(E)1,1 ) |
− 2 |
|
|
T1(E) := |
|
1 + |
i b |
− 2 |
||
|
|
|
|
k(E) |
|
||||||
|
|
|
|
|
|
|
|
|
|||
1 |
|
|
|
|
|
|
|
|
|
|
|
T2(E) |
|
|
|
|
|
|
|
|
|
|
|
T1(E) 0.5 |
|
|
|
|
|
|
|
|
|
|
|
0 0 |
5 |
10 |
|
15 |
|
20 |
|
25 |
30 |
||
|
|
|
|
|
E |
|
|
|
|
|
|
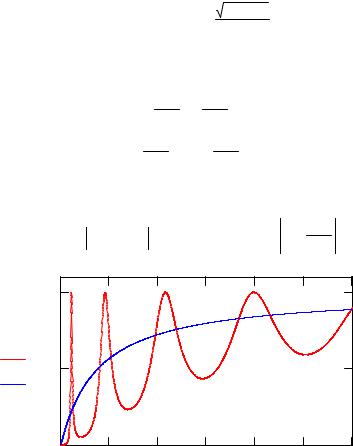
Рис. 5. Зависимости от энергии коэффициентов прохождения |
|||||||||||
через один δ- барьер (см. [8]) и через два таких же барьера |
|
||||||||||
|
|
|
38 |
|
|
|
|
|
|
|
|

Упражнения
1. Повторите символьные расчеты, получите выражения для коэффициентов отражения и прохождения и убедитесь в том, что при любой энергии имеет место условие нормировки вероятности
R(E) + T(E) = 1 .
2. В приближении широкого и высокого барьера (a Uo >> 1) получите соотношение
|
|
2 m (Uo − E) a |
||
Tth(E) = exp |
−2 |
|
. |
|
h |
||||
|
|
|
||
3. Рассчитайте коэффициенты отражения и прохождения, численно решая систему уравнений для коэффициентов волновых функций. Для этой цели можно использовать встроенную функцию lsolve(). Постройте графики рассчитанных зависимостей R(E) и T(E).
4. Теория α- распада атомных ядер, предложенная Г. Гамовым, основана на расчете в приближении ВКБ вероятности t(ε) подбарьерного туннельного перехода α- частиц в сферически симметричном потенциальном поле, образованном прямоугольной "ядерной" ямой и кулоновским барьером [6]. Рассчитайте зависимость периода полураспада T(ε) от энергии α- частиц в интервале [4 - 9] МэВ и сопоставьте с законом Гейгера-Неттола, например, для тория (Z = 90):
C = −51.94 |
logT(ε) = C + D |
D = 139.4 |
|
ε |
|
При расчете принять следующие параметры потенциала для тория: радиус R = 10фм, глубина ямы Uo = 25 МэВ и учесть, что период полураспада T(ε) и вероятность прохождения t(ε) связаны соотношением
T(ε)− 1 = exp ln |
h |
|
|
− t(ε) |
. |
|
|
2 |
|||||
|
|
|
|
|
||
|
m R |
|
|
|||
39
5. Проверьте следующие свойства матрицы распространения частицы в постоянном потенциале:
a)P(0) = 1 0 = P(r) P(−r) = I
0 1
b)P(r1)P(r2)= P(r1 + r2)= P(r2)P(r1)
с) |
P A = A P |
если |
|
|
|
− |
|
|
|
|
exp(i k a) = exp( i k a) |
||||||
|
в этом случае |
|
π |
и |
P = I |
или |
P = |
− |
|
|
k a = n |
|
|
I |
|||
6. Докажите следующие свойства матрицы скачка потенциала:
a) |
1 |
0 |
|
D12 D21 = D11 = I = |
0 |
1 |
|
|
|
||
b)D12 D23 = D13
с) |
D12 D23 = D23 D12 |
7. Проверьте следующие свойства матрицы δ- потенциала:
a) |
Del(α) Del(−α) |
1 |
0 |
= I = |
1 |
||
|
|
0 |
|
b) |
Del(α) = lim |
D21 P(a) D12 |
|
|
a → 0 |
|
|
при условии, что при U2 -> ∞
lim a (U2 − U1) = α a → 0
8. Покажите, используя матричный формализм, что коэффициент отражения частицы от потенциальной ступеньки, состоящей из одного скачка потенциала, равен
R = |
|
|
k1 − k2 |
|
2 |
|
|
||||
|
|
k1 + k2 |
|
|
|
|
|
|
40
