
Karmanov_Reznichenko
.pdf5. Рассчитайте уровни энергии и волновые функции в системе из двух близко расположенных потенциальных ям конечной глубины Ua , разделенных дополнительной ямой глубины Ub , отсчитываемой от уровня дна исходных потенциальных ям, если 0 < Ub < Ua. Сопоставьте результаты со спектром энергий частицы в одной потенциальной яме суммарной ширины.
6.Подготовьте программу и рассчитайте уровни энергии и волновые функции в системе из двух близко расположенных потенциаль-
ных ям, разделенных барьером конечной высоты Ub , отсчитываемой от уровня дна исходных потенциальных ям. Проанализируйте зависимость спектра и вида волновых функций от параметра непроницаемости потенциального барьера, пропорционального произведению высоты и ширины барьера.
7.Рассмотрим одномерную решетку, состоящую из 5 - 10 атомов. Каждому атому соответствует прямоугольная потенциальная яма. Все ямы отделены друг от друга равновысокими барьерами. Подготовьте программу и рассчитайте спектр энергий в системе и волновые функции нескольких состояний, принадлежащих каждой группе (зоне) близко расположенных уровней.
8.Предположим, что в подобной одномерной системе (упр. 7) один из атомов является нестандартным (примесь). Потенциальная яма, соответствующая данному атому, имеет ширину, большую или меньшую ширины потенциальных ям атомов решетки. Рассчитайте спектр энергий в такой системе и волновые функции нескольких состояний атома-примеси. Сравните полученный спектр энергий со спектром однородной цепочки атомов. Зависит ли положение уровня энергии атома-примеси в спектре от расположения его потенциальной ямы в решетке? Где локализована волновая функция атома - примеси? Зависят ли результаты от соотношения ширины ямы для атомапримеси и атома решетки?
9.Будем считать, что одномерная модель аморфного твердого тела представляет собой цепочку одинаковых потенциальных ям, разделенных барьерами переменной ширины. Задавая ширину барьеров согласно какому-либо правилу (или распределению случайных величин со средним значением, близким к ширине барьера однородной цепочки атомов), вычислите спектр энергий и сопоставьте его со спектром однородной цепочки атомов. Сохраняется ли и в этом случае "зонная" структура спектра?
11
|
|
Задача 2 |
|
|
|
|
|
|
Используя линейный вариационный метод Ритца рассчитать |
||||||||
уровни энергии ангармонического осциллятора с потенциалом вида |
||||||||
|
|
V(x) = α x2 − β x3 . |
|
|
|
|
||
|
|
Решение |
|
|
|
|
|
|
Потенциал и пробные функции |
|
|
||||||
Пусть параметры потенциала и масса частицы соответствуют |
||||||||
частоте колебаний молекулы |
водорода |
|
|
|
|
|||
ω = 7.8 1014 rad s− 1 |
α := 17.9 |
eV A− 2 |
|
β := 16 |
eV A− 3 |
|||
mc2 := 0.5 938.28 106 |
eV |
|
hc := 1.9732858 103 |
eV A |
||||
Потенциалы гармонического |
и ангармонического осциллятора: |
|||||||
V(x) := α x2 − β x3 |
|
Uo(x) := α x2 |
|
ω = |
2 |
α |
||
|
|
|
|
|
|
m |
||
6 |
|
|
|
|
|
λ = |
m ω |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
h |
|
4 |
|
|
|
|
|
λ := |
2 α mc2 |
|
V(x) |
|
|
|
|
|
|
hc |
|
|
|
|
|
|
|
|
|
|
Uo(x) |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
λ = 65.675 |
||
0 1 |
|
|
|
|
|
xo(λ) := |
2 |
|
0.5 |
0 |
0.5 |
1 |
λ |
||||
|
|
x,x |
|
|
xo(λ) = 0.175 |
|||
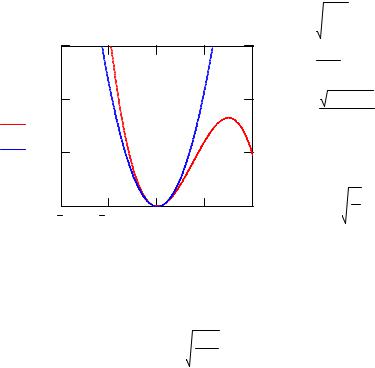
Рис. 1. |
Распределение потенциалов |
|
||||||
|
|
|
|
|||||
Область локализации волновых функций по x |
3 xo(λ) = 0.524 |
||
Уровни энергии гармонического осциллятора |
N := 4 |
||
|
|
2 α |
|
n := 0 .. N − 1 |
Ehon := hc |
mc2 (n + 0.5) |
|
12

Ортонормированные волновые |
функции |
первых |
|
N состояний |
||||||||||
гармонического осциллятора |
|
|
|
|
|
|
|
|||||||
|
1 |
|
|
|
|
|
|
|
|
(1 − 2 λ x2) |
||||
|
|
|
|
|
|
x2 |
|
|
||||||
λ |
4 |
|
|
−λ |
u2(x) := |
u0(x) |
||||||||
u0(x) := |
|
|
exp |
|
|
|
|
|
|
|||||
π |
|
|
|
|
|
|
2 |
|
|
|
2 |
|||
u1(x) := u0(x) x |
|
2λ |
|
|
|
u3(x) := u0(x) |
|
λ x (3 − 2 λ x2) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
и их вторые производные |
|
|
|
|
|
|
|
|
||||||
|
2 |
|
|
|
|
|
|
|
2 |
|
||||
du0(x) := |
|
|
d |
|
u0(x) |
|
|
du1(x) := |
|
d |
u1(x) |
|||
|
|
|
2 |
|
|
|
2 |
|||||||
|
|
dx |
|
|
|
|
|
|
|
dx |
||||
|
2 |
|
|
|
|
|
|
|
2 |
|
||||
du2(x) := |
|
|
d |
|
u2(x) |
|
|
du3(x) := |
|
d |
u3(x) |
|||
|
|
|
2 |
|
|
|
2 |
|||||||
|
|
dx |
|
|
|
|
|
|
|
dx |
||||
Выберем пробную функцию в виде
Φ(x) = c0 u0(x) + c1 u1(x) + c2 u2(x) + c3 u3(x),
где c0, c1, c2, c3 - варьируемые параметры.
В соответствии с общими положениями вариационного метода минимизируемый функционал в задаче на условный экстремум имеет вид
F(c0,c1,c2,c3,ε) = E(co,c1,c2,c3) − ε (Φ,Φ).
Здесь ε - неопределенный множитель Лагранжа, а среднее значение энергии определяется соотношением
(Φ H Φ)
E(c0,c1,c2,c3) = (Φ,Φ) .
Условие экстремума для квадратичного функционала - система линейных уравнений (см, например, [2] )
3 |
(Hj,k − ε Sj,k)cj = 0 |
|
∑ |
k = 0 ..3 |
j = 0
13
где Hj k и Sj k - матричные элементы гамильтониана H и интегралы перекрытия, определяемые соотношениями
|
|
⌠ |
∞ |
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
H |
j,k |
= |
|
−h |
u(x) |
d |
|
u(x) |
k |
+ V(x) u(x) u(x) |
k |
dx |
||||
2 m |
|
|||||||||||||||
|
|
|
|
j 2 |
|
|
|
j |
|
|||||||
|
|
⌡ |
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
− ∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S |
|
|
⌠∞ |
|
|
|
dx |
|
|
||
|
|
|
|
|
j,k |
= |
u(x) u(x) |
k |
|
|
||||||
|
|
|
|
|
|
|
⌡ |
|
|
j |
|
|
|
|||
|
|
|
|
|
|
|
|
− ∞ |
|
|
|
|
|
|
||
Как легко видеть, в силу ортонормированности волновых функций гармонического осциллятора, матрица S = I - единичной матрице.
Вычисление матричных элементов гамильтониана
|
|
|
|
|
|
u0(x) |
|
|
|
|
|
|
|
du0(x) |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U(x) := |
u1(x) |
|
|
|
d2U(x) := |
|
du1(x) |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
u2(x) |
|
|
|
|
|
|
|
du2(x) |
|
|
|
|
|
|
|||
|
|
|
|
|
|
u3(x) |
|
|
|
|
|
|
du3(x) |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
−hc2 ⌠∞ |
|
|
|
|
|
|
|
|
|
||
j := |
0 ..3 |
k := |
0 .. 3 |
Z |
j,k |
:= |
|
|
|
|
U(x) d2U(x) |
k |
dx |
||||||||||
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 mc2 ⌡ |
|
|
|
j |
|
|
|
|
|
||||
|
|
|
|
⌠∞ |
|
|
|
|
|
|
|
|
− ∞ |
|
|
|
|
|
|
|
|
||
W |
|
|
:= |
U(x) V(x) U(x) |
|
dx |
|
H |
|
|
:= Z |
|
+ W |
|
|
||||||||
j,k |
|
k |
|
j,k |
j,k |
j,k |
|||||||||||||||||
|
|
⌡ |
|
|
j |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
− 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.273 |
|
|
−0.032 |
|
6.01 × 10 |
− 9 |
|
0.026 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
−0.032 |
|
0.818 |
|
|
0.09 |
|
|
|
8.217 × |
10 |
− 12 |
|
|||||||
H = |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
− 12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
4.528 × |
10 |
0.09 |
|
|
1.363 |
|
|
|
−0.166 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
0.026 |
|
8.165 × 10 |
− 12 |
−0.166 |
|
|
|
1.908 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
14
Собственные значения и собственные векторы
Вычислим собственные значения и соответствующие им векторы, используя встроенные функции eigenvals() и eigenvecs(), и сравним результаты со значениями уровней энергии первых 4-х состояний гармонического осциллятора. Отметим, что функция eigenvecs() возвращает матрицу, составленную из собственных векторов.
0.27
0.804 G := eigenvals(H) G =
1.9551.331
Внимание! Порядок собственных значений, возвращаемых функцией eigenvals(), не соответствует порядку рассчитываемых состояний. Поэтому собственные значения и, конечно, собственные векторы следует упорядочить.
G := sort(G) |
|
|
0.27 |
|
0.273 |
|||
G = |
|
0.804 |
|
Eho = |
0.818 |
|
||
|
||||||||
C := eigenvecs(H) |
|
1.331 |
|
|
|
|||
|
|
|||||||
|
|
|
|
|
1.363 |
|
||
|
|
1.955 |
|
|
1.908 |
|||
Перестановка 3-го и 4-го столбцов в матрице из собственных векторов.
k := 2 .. 3 |
j := 0 ..3 |
caj,k := Cj,k |
Cj,2 := caj,3 |
Cj,3 := caj,2 |
|
Проверка правильности нахождения собственных векторов - расчет невязки системы уравнений. Отметим, что найденные собственные векторы уже нормированы на единицу.
|
0 |
0 |
0 |
0 |
|
j := 0 ..3 δC j := H C j − G C j |
δC = 0 |
0 |
0 |
0 |
|
j |
|
0 |
0 |
0 |
|
|
0 |
|
|||
|
0 |
0 |
0 |
0 |
|
15
QRразложение
Воспользуемся встроенной функцией qr() для преобразования исходной матрицы H и приведения ее к матрице треугольной или жордановой структуры.
B := qr(H)
Полученная матрица B содержит две матрицы Q и R и представляет матрицу H в виде произведения H = QR.
Q := submatrix(B,0,3,0,3)
|
0.989 |
|
|
0.114 |
9.798 × 10− 4 |
0.096 |
||||
|
−0.116 |
|
0.987 |
0.109 |
0.017 |
|
||||
Q = |
|
|
|
− 11 |
|
|
|
|
|
|
|
1.643 × |
10 |
0.111 |
−0.986 |
−0.121 |
|
||||
|
|
|
|
|||||||
|
0.094 |
|
|
0.015 |
0.123 |
−0.988 |
||||
|
|
|
R := |
submatrix(B,0,3,4,7) |
|
|
||||
|
|
0.276 |
−0.126 |
−0.026 |
0.206 |
|
||||
|
R = |
|
0 |
|
0.814 |
0.238 |
0.013 |
|
||
|
|
0 |
|
0 |
−1.355 |
0.398 |
|
|
||
|
|
|
|
|||||||
|
|
|
|
|
|
|||||
|
|
|
0 |
|
0 |
0 |
−1.862 |
|
||
Здесь матрица Q ортогональна, а матрица R , очевидно, верхняя треугольная. Проверим правильность разложения:
1 0 |
0 |
0 |
0 0 |
0 |
0 |
||||
QT Q = 0 |
1 |
0 |
0 |
H − Q R = 0 |
0 |
0 |
0 |
||
|
0 |
1 |
0 |
|
|
0 |
0 |
0 |
|
0 |
|
0 |
|
||||||
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
||
Использование QR -разложения для нахождения собственных значений и векторов основано на итерационном процессе вычисления преобразованной матрицы Hk+1 с использованием Qk и Rk матриц:
16

Bk = qr(Hk) |
|
Hk = Qk Rk |
|
Hk+1 = Rk Qk |
|
λ(H) j = lim |
λ H |
= lim |
( |
H |
j = 0 .. N − 1 |
k → ∞ |
( k) |
k → ∞ |
|
j, j)k |
|
Следующая подпрограмма, основанная на итерационном использовании встроенной функции qr(), возвращает диагональные элементы последней преобразованной матрицы. Здесь а - исходная матрица размерности n, eps - требуемая точность расчета собственных значений, и δm > eps - начальное значение модуля разности для диагональных элементов матрицы ak на соседних итерациях.
EigVals(n,a,eps,δm) := for j 0 .. n − 1 adj ← aj, j
jr ← rows(a) − 1 kc ← 2 jr + 1 while δm > eps
b ← qr(a)
q← submatrix(b,0, jr,0, jr)
r← submatrix(b,0, jr, jr + 1,kc)
a← r q
for |
j 0 .. n − 1 |
|
|
|
|
||||||||
|
|
δj ← |
|
ad |
− a |
j, j |
|
|
|
||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
j |
|
|
|
|
||
|
|
adj ← aj, j |
|
|
|
|
|
||||||
δm |
← max(δ) |
|
|
|
|
|
|||||||
ad ← sort(ad) |
|
|
|
|
|
|
|||||||
ad |
|
|
|
|
|
|
|
|
|
|
|
||
Gqr := EigVals(4,H,0.0001,1) |
|
|
0.27 |
|
|
|
0.27 |
||||||
|
|
0.804 |
|
|
|
|
0.804 |
|
|||||
Gqr = |
|
G = |
|
||||||||||
|
1.331 |
|
|
1.331 |
|
||||||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1.955 |
|
|
|
1.955 |
|
|||||
17
Собственные значения, рассчитанные двумя разными способами, совпадают. Для того, чтобы найти собственные векторы C исходной матрицы следует найти собственные векторы Ck последней преобразованной матрицы Hk и умножить их на произведение ортогональных матриц Qk , использовавшихся при преобразовании.
C = (Q0 Q1 ..Qk)Ck
Волновые функции ангармонического осциллятора
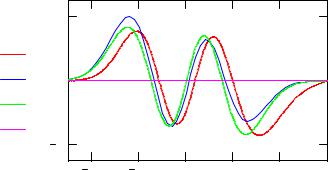
Согласно решению данной задачи в рамках вариационного метода, влияние ангармонизма приводит к смещению вниз нижних энергетических уровней по сравнению с уровнями гармонического осциллятора, однако точность самого вариационного расчета обычно падает с ростом номера состояния. Чем выше состояние по энергии, тем больше пробные функции отличаются от истинных волновых функций. На рисунке 2 сплошной линией показана точная волновая функция как решение уравнения Шредингера, штриховой - из вариационного расчета и пунктиром - базисная функция 3-го состояния.
GT = ( 0.27 |
|
0.804 |
1.331 1.955 ) |
|
|
3 |
EhoT = ( 0.273 0.818 1.363 1.908 ) |
|
|||||
Φ(n,x) := ∑ Cj,n U(x) j |
||||||
EcT = ( 0.27 |
0.802 |
1.319 1.819 ) |
|
|
j = 0 |
|
|
2 |
|
|
|
|
|
ψi |
|
|
|
|
|
|
Φ(3,x) |
|
|
|
|
|
|
u3(x) |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
0.4 |
0.2 |
0 |
0.2 |
0.4 |
|
|
|
|
Xi ,x,x |
|
|
Рис.2. Волновая и пробная функции 3-го возбужденного состояния |
||||||
|
|
|
18 |
|
|
|

Упражнения
1.Объясните, почему диагональные матричные элементы оператора H совпадают в нашем расчете со спектром гармонического осциллятора.
2.Рассчитайте собственные значения гамильтониана H как корни характеристического или векового уравнения
D(E) = H − E I = 0 ,
где I - единичная матрица 4-го порядка. Проведите графический анализ расположения корней и вычислите корни, используя встроенную функцию root().
3. Используя встроенную функцию lsolve(), найдите собственные векторы C из решения системы уравнений
3 |
(Hj,k − E δj,k)cj = 0 , |
|
∑ |
k = 0 ..3 , |
j = 0
4.Проверьте положительную определенность матрицы H гамильтониана и найдите собственные векторы, решая систему уравнений c симметричной матрицей с помощью встроенной функции cholesky().
5.Рассчитайте собственные значения и собственные векторы для гамильтониана данной задачи итерационным методом, используя QR - разложение.
6.Проверьте нормировку и ортогональность рассчитанных волновых функций.
7.Согласно теореме вириала для гармонического осциллятора, среднее значение кинетической энергии в каждом состоянии равно среднему значению потенциальной энергии в этом же состоянии. Проверьте, выполняется ли эта теорема для состояний с рассчитанными волновыми функциями ангармонического осциллятора.
8.Используя линейный вариационный метод Ритца и волновые функции гармонического осциллятора, рассчитайте уровни энергии первых 4-х состояний частицы в потенциале вида
V(x) = α x2 + β x .
19
|
|
|
Задача 3 |
|
|
|
Частица массы |
m находится в бесконечно глубокой симмет- |
|||||
ричной потенциальной яме на отрезке -1< x < 1. |
Требуется найти |
|||||
вариационным методом допустимые значения энергии частицы в |
||||||
первых трех состояниях, используя для построения пробной функ- |
||||||
ции следующие соотношения: |
|
|
|
|||
|
|
Φ(x) = c0 u0(x) + c1 u1(x) + c2 u2(x) , |
||||
|
|
u0(x) := 1 − x2 , |
u2(x) := 1 − x4 , |
|||
|
|
|
u1(x) := x (1 − x2). |
|
|
|
|
|
|
Решение |
|
|
|
|
|
|
Система линейных уравнений |
|||
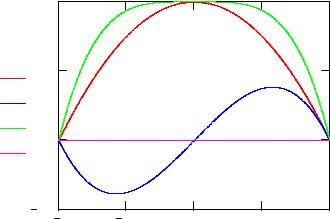
Семейство функций u0(x),u1(x),u2(x) не является ортонормированным. |
||||||
Действуя в рамках общей схемы вариационного метода (см. задачу 2), |
||||||
получаем систему линейных уравнений |
|
|
||||
|
1 |
|
|
|
|
|
u0(x) |
0.5 |
|
|
|
|
|
u1(x) |
|
|
|
|
|
|
u2(x) |
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
0.5 |
1 |
0.5 |
0 |
0.5 |
1 |
|
|
|
|
x |
|
|
|
|
Рис. 1. Базисные функции системы |
||||
|
|
|
|
20 |
|
|
