ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ

Т.Н. Т и т о в а

ПРОИЗВОДНАЯ ФУНКЦИИ И ЕЕ ПРИМЕНЕНИЕ В ИНЖЕНЕРНОМ ВУЗЕ

УЧЕБНОЕ ПОСОБИЕ

М о с к в а 2010

УДК 517(075.8)

Титова Т.Н. Производная функции и ее применение в инженер-

ном вузе: Учебн. пос. / Моск. гос. строит. ун-т.-М.: МГСУ, 2010.- 80 с.

Пособие посвящено дифференциальному исчислению функции одной переменной. Рассмотрены основные вопросы теории, разобрано большое количество примеров и задач.

Пособие предназначено для студентов 1 курса, обучающихся по направлению 270100 «Строительство».

Научный редактор:

канд. физ.-мат. наук, проф. В.Н.Арефьев

Рецензенты:

ведущий научный сотрудник Математического института им. В.А.Стеклова РАН, докт. физ.-мат. наук О.К.Шейнман,

научный сотрудник лаборатории «Разностные методы» фак-та ВМК МГУ им. М.В.Ломоносова,

канд. физ.-мат. наук Т.Я. Ершова

2

§1. ПРОИЗВОДНАЯ ФУНКЦИИ

Понятие производной является одним из основных математических понятий. Оно возникло при решении ряда задач, важнейшими из которых является задача о скорости неравномерного движения и задача о касательной к кривой. Производная широко используется при решении задач математики, физики, других наук, в особенности при изучении скорости разных процессов.

1.1. Задача о скорости

Пусть материальная точка движется по некоторой прямой. Через S обозначим расстояние данной точки от некоторого

Это равенство называется законом движения точки.

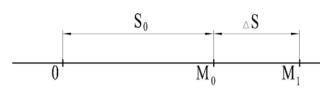
Пусть в момент времени t0 точка занимает положение M0 на расстоянии S0 от начального положения, а в некоторый следующий момент времени t =t0 + t точка займет положение М

на расстоянии S0 + S от начального положения (рис. 1).

Рис. 1

Рассмотрим среднюю скорость движения точки за время ∆t (на участке M0M ):

vср = St .

Средняя скорость зависит от значения ∆t: чем меньше ∆t, тем точнее средняя скорость выражает скорость движения точки в момент времени t0.

3

Скоростью движения точки в момент времени t0 называ-

вается предел отношения приращения функции к приращению аргумента при x →0

Если производная существует во всех точках некоторого промежутка (a,b), то её можно рассматривать как новую функцию f ′(x). Операция нахождения производной от функции f(x)

называется дифференцированием этой функции.

В задаче о скорости прямолинейного движения точки была получена формула

Это равенство перепишем в виде

v = S′(t).

Таким образом, скорость прямолинейного движения материальной точки в момент времени t есть производная от пути S по времени t. В этом заключается механический смысл производной.

4

1.3. Геометрический смысл производной. Уравнение касательной и нормали к кривой

Возьмем на непрерывной кривой L две точки M0 и М (см. рис. 2). Прямую М0М , проходящую через эти точки, называют секущей. Пусть точка М приближается по кривой к точке М0, тогда секущая М0М занимает разные положения.

Рис. 2

Определение. Касательной к кривой L в точке М0 называется предельное положение М0Т секущей М0М , когда точка М неограниченно приближается по кривой к точке М0.

Рассмотрим график непрерывной функции y = f (x) ,

имеющей в точке М0(х0,f(x0)) невертикальную касательную. Пусть α - угол, образованный касательной с положительным направлением оси Оx, y0=f(x0). Рассмотрим на графике другую точку М1(х0+∆х, у0+∆у). Проведем секущую М0М1. Пусть ϕ - угол, образованный секущей с положительным направлением оси Оx.

Из ∆М0М1С видно, что tgϕ = yx (см. рис. 3).

Пусть x →0 , тогда точка М неограниченно приближается по кривой к точке М0, секущая М0М стремится занять положение касательной М0Т, угол ϕ →α . Тогда угловой коэффициент ка-

сательной

5

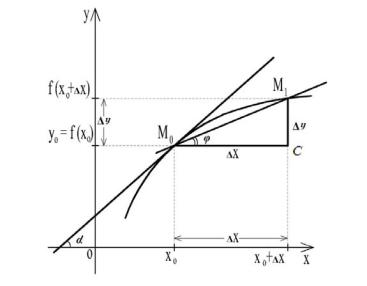
Рис. 3

Таким образом, значение производной f ′(x0 ) равно угло-

вому коэффициенту касательной к графику функции f(x) в соответствующей точке М0(х0, f(х0)).

Уравнение касательной

Воспользуемся уравнением прямой, проходящей через

Уравнение нормали

Нормалью к кривой L в точке М0(х0,y0) называется прямая, проходящая через точку М0 и перпендикулярная касательной в этой точке (рис. 4).

6