
bardushkin
.pdf
x 0, FX
II Случай
x |
x |
0 dt |
|
|
|
0
.
|
0 |
|
|
x |
|
|
|
x |
|
|
|
|
x 0, FX x 0 dt e |
t |
dt e |
t |
e |
x |
1 |
||||||
|
||||||||||||
|
|
0 |
|
|||||||||
|
|
|
0 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||||
0, x 0 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
FX x |
e x |
, x |
0 |
|
|
|
|
|
|
|
||
1 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
(x) |
|
|
|
|
|
|
|
|
||
|
X |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
x
h |
|
|
ln 2 |
|
X |
|
|||
|
|
|||
|
|
|
Показательное распределение тесно связано с простейшим стационарным Пуассоновским потоком событий.
Покажем, что интервал времени Т между двумя соседними событиями в простейшем потоке, имеет показательное распределение с параметром равным интенсивности потока.
t
|
0 |
Найдем |
|
F |
t |
T |
|
t T
FT t .
P T t
Для того, чтобы подсчитать эту вероятность нужно, чтобы хотя бы одно событие потока попало на участок длины t.
P 1 P 1 e t |
|
|
|
0 |
|
|
|
F t 1 e t |
|
|
|
T |
|
|
|
Продифференцировав |
FT t , получим |
fT t e |
t |
|
Показательное распределение играет большую роль в Марковских случайных процессах, теории массового обслуживания и теории надежности.
П р и м е р .
Время безотказной работы ЭВМ – это СВ Т, имеющая показательное распределение с параметром . Физический смысл – это среднее число отказов в единицу времени, если не учитывать простоев ЭВМ. Из-
вестно, что ЭВМ уже проработало без отказов время . Найти при этом условии плотность распределения |
||
f t времени T |
(время, которое ЭВМ проработает после момента , до ближайшего отказа). |
|
Решение. |
|
|
|
|
+ t |
|
|
|
0 |
|
t |
|
|
t |
Так как простейший поток отказов не имеет последствия, то вероятность появления хотя бы одного отказа на участке (, + t) не зависит от того, появлялись ли отказы ранее момента .

Найдем
f |
|
t |
|
|
Вывод:
F |
t P T |
|
|
|
|
e |
t |
|
|
||
t 1 e |
t |
|
.
Таким образом распределение времени, оставшегося до следующего отказа, не зависит от того, сколько времени ЭВМ уже отработало без отказов.
§ 3. Нормальное распределение
О п р е д е л е н и раметрами m R и
е |
. СВНТ Х называется распределенной по нормальному (Гауссовскому) закону с па- |
0 |
, если плотность распределения вероятности имеет вид. |
|
|
|
|
|
|
x m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
x |
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
f |
|
e |
|
2 |
, x |
|
|
|
|
|
|
|
|||||
X |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Нормальное распределение задается двумя параметрами m и . |
|
|
|
|
|||||||||||||
X ~ N m, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Докажем, что m mX , X – ? |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
mX |
x f X x dx |
1 |
|
x e |
|
2 |
2 |
dx |
||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
z |
x m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
x |
z m |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Пределы интегриров ания |
|
|
|
|
|
||||
Д о к а з а т е л ь с т в о : |
|
не изменяются |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
z m e |
|
2 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
d z m
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
2 |
|
|
|
|
|
|
|
|
z |
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
dz |
|
m |
|
e |
|
|
|
dz m |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
2 |
|
|
|
2 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нечетная |
|
|
|
функция в симметричн |
|
|
ых пределах |
|
интеграл |
Пуассона |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
" |
|
|
|
|
|
|
|
|
|
|
|
|
|
равен |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x m 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
DX |
1 |
|
|
|
|
|
|
x m |
2 |
|
e |
2 2 |
|
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
z |
x m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
x z m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z 2 |
e |
2 |
|
|
dz |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
Пределы |
интегриров ания |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
не изменяются |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
z2 |
|
|
z 2 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
z2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
z e |
|
|
2 |
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z e |
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
2 |
|
|
|
|
z |
|
|
|
2 |
|
|
|
|
|
|
z2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
e |
2 |
|
d z |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
z |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
e 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||

X
.
Лекция № 12
|
|
|
|
|
|
|
|
|
|
|
x m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
x |
|
1 |
|
|
|
|
|
|
2 |
|
|
f |
|
|
|
|
e |
|
2 |
, x |
|||||
X |
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
X ~ N m, |
|
|
|
|
|
|
|
|
|||||
X ~ N 0,1 |
– стандартизованная нормальная величина. |
||||||||||||
f X x |
1 |
|
|
|
|
x2 |
|
|
|
|
|||
|
|
e |
2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
Функция распределения стандартизованной нормальной величины.
|
|
|
|
|
|
x |
|
t |
2 |
|
|
|
|
|
|
|
x |
1 |
|
|
|
|
|
|
|
|
|
|
|
||||
|
e |
2 |
dt |
|
|
|
|
|||||||||
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1 x |
|
|
|
|
|
t m |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
FX x |
|
1 |
|
|
|
|
|
|
|
dt |
|
|
||||
|
|
|
|
e |
|
|
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
F |
|
x |
x |
m |
|
|
|
|
|
|
|
|
||||
X |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
P x X x |
|
|
|
|
x |
|
m |
x |
m |
|||||||
2 |
|
|
2 |
|
|
1 |
|
|
||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
П р и м е р . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Дана СВ Х, |
X ~ N 30,10 . Найти вероятность попадания P 10 X |
|||||||||||||||
50
.
Решение.
P 10 X |
||
|
2 |
1 |
|
|
|
50 30 |
|
10 30 |
|
2 2 |
||
50 |
|
|
|
|
|
|
|
10 |
|
|
10 |
|
|
2 2 2 1 2 0,9772 1 0,9544 |
||||||
Часто требуется вычислять вероятность того, что отклонение нормально распределенной СВ Х от МО по абсолютной величине меньше заданного положительного числа .
P X mX – ?
X P  X
X
P  X
X
m |
X |
X m |
X |
, |
m |
X |
X m |
X |
|
||||||||||||||||
|
|
P m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
m |
X |
X |
X m |
X |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
m |
X |
m |
X |
|
|
|
m |
X |
m |
X |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
m |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
X |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Методами математического анализа можно легко построить график плотности

f |
(x) |
|
X |
1 |
|
2 |
|
0 |
m |
S = 1
m – сдвиг по оси 0Х
– параметр островершинности  fX(x)
fX(x)
x
Гауссова кривая:
0 |
m |
x |
З а м е ч а н и е .
Мода и медиана совпадают с МО.
§ 4. Оценка отклонения теоретического распределения от нормального; асимметрия и эксцесс
При изучении распределений, отличных от нормального, возникает необходимость количественно оценить это различие. С этой целью вводят специальные характеристики (асимметрию и эксцесс).
a X 33X
e 4 3
X |
4 |
|
|
|
X |
Для нормального распределения эти характеристики равны 0, поэтому, если для изучаемого теоретического распределения асимметрия и эксцесс имеют небольшие значения, то можно предположить близость
этого распределения к нормальному. Наоборот большие значения a X клонения от нормального.
fX(x)
aX > 0
и |
e |
X
, указывают значительные от-
0 |
dX |
x |
Пологая часть правее моды, значит a X 0 .
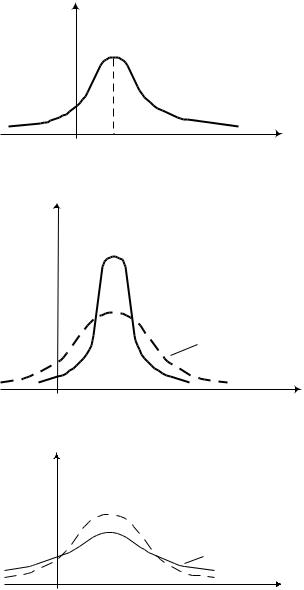
f |
(x) |
|
X |
a |
X |
> 0 |
|
|
0 |
d |
X |
x |
|
|
|
Пологая часть левее моды, значит
f |
(x) |
|
X |
e |
X |
> 0 |
|
|
aX
0
.
|
кривая нормального |
||
|
распределения |
||
0 |
|
|
x |
f |
(x) |
|
|
|
X |
|
|
|
|
кривая нормального |
|
|
|
|
распределения |
|
e |
|
<0 |
|
X |
|
|
0 |
|
|
x |
З а м е ч а н и е .
При исследовании эксцесса надо считать, что нормальное исследуемое распределение, имеют одинаковое МО и дисперсию.
Глава VII. Системы случайных величин (случайные векторы)
Пусть на одном и том же вероятностном X1 X1 ,..., X n X n , совокупность X1; X 2 ;...; X случайным вектором.
П р и м е р ы .
n
пространстве ( ,A, P) задано n СВ,
– называется многомерной (n-мерной) СВ или
Широта X и долгота Y падения метеорита на Землю представляет собой двумерный случайный вектор
X ,Y . В эту модель можно ввести третью координату Z – это время от начала наблюдения до падения пер-
вого метеорита на Землю. Тогда X ,Y , Z .
Успеваемость студента, окончившего курс обучения в ВУЗе, характеризуется n – случайных величин, проставленных по 5-ти бальной системе.
§ 1. Совместная функция распределения

Рассмотрим в одном и том же вероятностном пространстве ( ,A,P) набор СВ
X |
; |
1 |
|
X |
;...; X |
n |
i |
|
. Так как
множество
X k
x |
|
k |
|
A, таких пересечения
n |
X |
|
|
|
k |
||
|
|||
k 1 |
|
|
x |
|
k |
|
A, поэтому существует вероятность этого
события, которая называется многомерной функцией распределения.
P X1 x1, X 2 x2 ,..., X n xn F x1, x2 ,..., xn . |
|
З а м е ч а н и я : |
|
1.В дальнейшем ограничимся случаем двух случайных величин |
X1 X , X 2 Y |
2. Функция F x, y P X x,Y y – вероятность того, что случайная точка X |
|
нечный квадрант с вершиной в точке x; y . |
|
Y |
|
. ,Y
попадает в беско-
(x, y)
X
С помощью F, можно вычислить вероятность попадания случайной точки в полуполосу или в прямоугольник.
а)
|
Y |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
x1 |
x2 |
X |
|
||
P x |
X x |
2 |
,Y y F x |
2 |
, y F x |
, y |
|
1 |
|
|
|
1 |
|
||
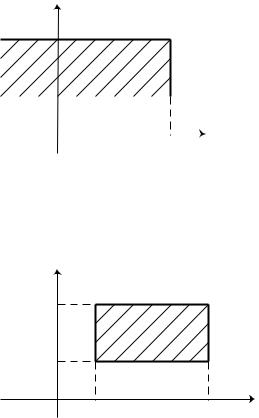
б)
Y
y2
|
|
|
|
y1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
X |
|
|
|
|
|
|
||
P X x, y |
Y y |
2 |
, F x, |
y |
2 |
F x, y |
|
|
|
||||||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||
в) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
x2 |
|
X |
|
|
|
|
P x |
X x |
2 |
, y |
Y y F x |
2 |
, |
y |
2 |
F x |
, y |
2 |
|
|||||||||||
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||
F x |
2 |
, |
y |
F x |
, |
y |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
1 |
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
П р и м е р . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
F x, y sin x sin y |
|
|
|
|
|
|
|
|
|
|
|
|||||||
0 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
X |
|
, |
|
Y |
|
|
|
sin |
|
sin |
|
sin |
|
|
|
||
P |
|
|
|
|
sin |
|
|
|
|
|
||||||||
|
6 |
|
|
2 4 |
|
3 |
|
2 |
|
3 |
|
6 |
|
3 |
|
|
||

|
|
sin |
|
sin |
|
sin |
|
|
|
3 |
|
3 |
|
|
2 |
sin |
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
4 |
|
6 |
|
4 |
|
2 |
|
4 |
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||
2 |
|
|
|
|
|
4 |
|
|
|
|
|
3 |
2 |
4 |
|
|
|
|
Из формулы вероятности попадания в прямоугольник и определения многомерной функции распреде- |
|
ления |
F x, y , вытекают следующие свойства, которые доказываются аналогично одномерному случаю. |
Свойства. |
|
1. |
F x, y по каждому аргументу не убывает и непрерывна слева. |
2. |
F , y F x, F , 0 . |
3. |
F , 1. |
4. а) При y , F x, y становится функцией распределения компоненты x. |
|
F x, FX x .
б) При x , F x, y становится функцией распределения компоненты y.
F , y FY y .
§ 2. Дискретные двумерные случайные величины
О п р е д е л е н и е . Двумерная СВ (X, дискретной.
Пусть СВ Х может принимать значения
Y)
x |
, |
1 |
|
называется дискретной, если каждая из СВ и Х и Y является
..., xn , а СВ Y принимает дискретные значения |
y1,..., ym . |
|
|
|
|
Y |
y1 |
y2 |
|
… |
|
ym |
P{X=xi} |
|
|
|
|
|
X |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
P11 |
P12 |
|
… |
P1m |
P1 |
|
|
|
|
|
|
|
x2 |
P21 |
P22 |
|
… |
P2m |
P2 |
|
|
|
|
|
|
|
… |
… |
… |
|
… |
|
… |
… |
|
|
|
|
|
|
xn |
Pn1 |
Pn2 |
|
… |
Pnm |
Pn |
|
|
|
|
|
|
P{Y=yj} |
P 1 |
P 2 |
|
… |
P m |
|
|
|
||
Двумерный |
случайные |
вектор |
может |
|
принимать |
только |
пары |
значений |
|||||
X ,Y xi ; y j i 1,..., n; |
j 1,..., m |
|
|
|
|
|
|
|
|
||||
P |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
ij |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
m |
|
|
|
|
|
|
|
|
|
|
|
|
P i j 1 |
|
|
|
|
|
|
|
|
|
|
|||
i 1 |
j 1 |
|
|
|
|
|
|
|
|
|
|
|
|
По этой таблице нетрудно определить функцию распределения.
F x, y |
Pij |
|
|
|
|
|
i:xi x; |
|
|
|
|
|
j: y j y |
|
|
|
|
P X ;Y B |
|
Pij |
|||
|
|
x |
; y |
j |
B |
|
|
i |
|
|
|
.
Лекция № 13
|
Y |
–1 |
1 |
Pi |
X |
|
|||
|
|
|
|
|
0 |
|
0,1 |
0,06 |
0,16 |
1 |
|
0,3 |
0,18 |
0,48 |
2 |
|
0,2 |
0,16 |
0,36 |
P j |
|
0,6 |
0,4 |
1 |

Найти одномерные законы распределения компонент X и Y. |
|
Найти вероятность того, что |
P X Y – ? |
F x, y – ? |
|
Решение.
P X
P X P X
0
1
2
P
1
P2 P3
0,16
0,48 0,36
X |
0 |
1 |
2 |
P |
0,16 |
0,48 |
0,36 |
P Y P Y P X
F x,
1 P 1 0,6
1 P 2 0,4
Y 1 P X Y 1 0,06 0,94
 Y
Y
1 






1 |
2 |
x |
-1


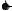



y P X x, Y y
Y |
y –1 |
–1 < y 1 |
y > 1 |
|
X |
||||
|
|
|
||
x 0 |
0 |
0 |
0 |
|
0 < x 1 |
0 |
0,1 |
0,16 |
|
1 < x 2 |
0 |
0,4 |
0,64 |
|
x > 2 |
0 |
0,6 |
1 |
§ 3. Непрерывные двумерные СВ
Пусть A – -алгебра множеств двумерного пространства R2, порожденная всевозможными прямоугольниками вида
a |
x b |
1 |
1 |
a2 |
y b2 . |
О п р е д е л е н и е .
Двумерной плотностью
P X ;Y B f x, y dx B
распределения
dy , где B A
f x, y называется такая функция, что вероятность
.
Из определения
Свойства.
I. f x, y 0 .
f x, y
следуют ее свойства.

|
|
f x, y dx dy 1 |
|
|
|||||
II. |
|
(условие нормировки). |
|||||||
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
F x, y |
x |
|
y |
f u1 |
|
|
du1 du2 . |
|
III. |
|
|
, u2 |
||||||
|
|
|
|||||||
|
|
|
|
|
|
|
|
||
|
f x, y |
|
2 |
F x, y |
|
||||
IV. |
|
|
|||||||
|
|
x y |
|
. |
|
||||
|
|
|
|
|
|
|
|
||
О п р е д е л е н и е .
Двумерная СВ (X; Y) называется непрерывной, если ее распределение имеет f x, y .
П р и м е р 1 :
f |
x, y |
|
|
1 |
|
|
1 |
1 y |
|
|
|
|
|
|
|
|
||||
|
2 |
x |
2 |
2 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
F x, y – ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
F x, y |
1 |
|
|
|
y |
|
x |
|
|
|
|
1 |
|
|
|
|||||
|
|
|
du2 |
|
|
|
|
|
|
du1 |
|
|||||||||
|
|
|
1 u 2 |
1 u 2 |
||||||||||||||||
2 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
||
|
1 |
arctg u |
|
x |
|
arctg u |
|
y |
|
|
|
|||||||||
|
|
|
|
|
2 |
|
|
|
|
|||||||||||
|
|
2 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
2
|
|
|
arctg x |
|
arctg y |
|
2 |
|
2
.
П р и м е р 2 : (двумерное равномерное распределение)
Плотность |
f x, y равномерного распределения на области S R2 конечной двумерной площади |
||
|
1 |
, x; y S |
|
|
|
|
|
f x, y S |
|
|
|
|
|
|
|
0, x; y S |
|
||
|
|
|
|
|
|
z |
|
|
|
1 |
h |
|
|
S |
|
|
|
B |
y |
|
|
|
|
x |
|
S |
|
P X ;Y B  B S
B S 
S
 S
S
 .
.
