
bardushkin
.pdf
Ar n
n n 1 ... |
n r 1 |
n! |
, r |
|
n r ! |
||
|
n
.
Доказательство:
Каждое <n,r>-размещение без повторений является упорядоченной последовательностью длины r. По правилу произведения получаем
Ar n n 1 ... n r 1 |
n! |
|
. |
|
n r ! |
||||
n |
|
|||
|
|
|
||

Теорема 3.
|
|
|
A |
r |
|
n! |
, r n . |
|
C |
r |
|
|
|
||||
n |
r! n r ! |
|||||||
|
|
|
|
|||||
|
n |
|
r! |
|
|
|||
|
|
|
|
|
||||
Доказательство:
Каждое <r,r>-сочетание без повторений можно упорядочить r!-способами.
Объединение получаемых таким образом попарно непересекающихся множеств <n,r>-размещений без повторений для всевозможных <n,r>-сочетаний без повторений, даст все <n,r>-размещения без повторений.
Ar r! (суммирование производится по всевозможным <n,r>-сочетаниям без повторений). n
|
|
r |
|
|
A |
|
|
n |
C |
r |
|
|
|
|
|
n |
|
Теорема 4.
r! |
r!C |
|
||||
|
|
|
|
r |
|
|
|
|
|
|
n |
|
|
A |
r |
|
|
n! |
|
|
|
|
|
. |
|||
n |
r! n r ! |
|||||
|
|
|||||
r! |
|
|
||||
C r n
r |
n 1 |
= Cr n 1 |
Cr n 1 |
Пример
X 1,2,3,4 , n 4, r 6 B 2;2;3;3;3;4 .B 0110111016 4 1
Пример
C 110011011
C 1;1;3;3;4;4 .
Доказательство:
Каждому <n,r>-сочетанию (В) с повторениями, составленного из элементов множества X поставим в соответствие вектор B длины r+n–1, состоящего из r-единиц и n–1нулей, такой, единиц между (i–1)-м и i-м нулями, где 2 i n–1 будет равно числу элементов Xi , входящих в
x |
,..., x |
1 |
n |
что число сочетание
В.
Число единиц, стоящих перед первым нулем равно числу элементов |
x1 |
, а число единиц, стоящих после |
(n–1) нуля равно числу элементов xn , входящих в В.
Это соответствие между В и B B B будет взаимнооднозначным.
Поэтому, чтобы подсчитать количество <n,r>-сочетаний с повторениями достаточно подсчитать количество векторов B .
Количество векторов B
Cnr =
r |
|
C |
n 1 |
r |
n 1 |
|
C |
1 |
r n |
.
Лекция № 3
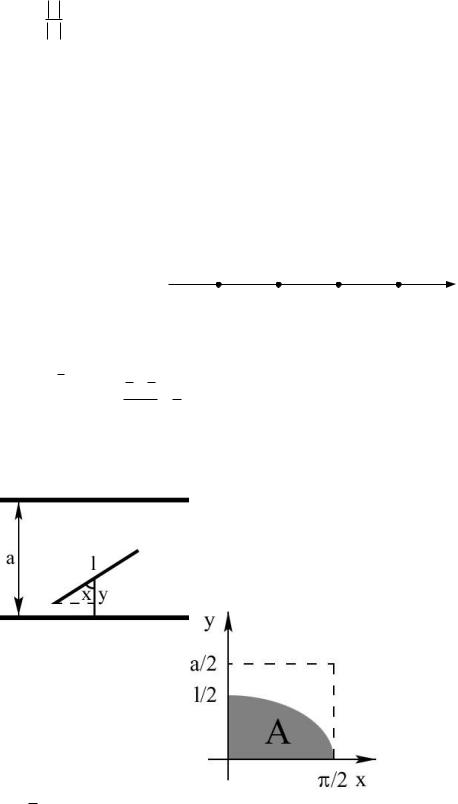
§ 6. Геометрические вероятности
Геометрические вероятности – класс моделей вероятностных пространств, дающий геометрические вероятности.
Пусть Ω={ω} – ограниченное множество n-мерного евклидова пространства с конечным n-мерным объёмом.
Событиями назовём подмножества Ω, для которых можно определить n-мерный объём.
Для любого A A положим
P A |
A |
|
|
||
|
, где |V|-n-мерный объем множества V A.
Это вероятностное пространство служит моделью задач, в которых частица случайно бросается в область Ω. Предполагается, что положение частицы равномерно распределено на множестве Ω, т. е. вероятность попадания частицы в подмножество A пропорциональна n-мерному объёму этой области.
З а м е ч а н и е .
В классе конечных вероятностных пространств в систему A входили все подмножества Ω. При геомет-
рическом определении вероятности в качестве A уже нельзя взять все подмножества Ω, так как некоторые из них не имеют n-мерного объёма.
П р и м е р ы
1 . Стержень разламывается на две части в случайной точке, равномерно распределённой по длине стержня. Найти вероятность того, что длина меньшего обломка окажется не больше трети длины всего стержня.
0 |
l |
Обозначим за x расстояние от фиксированного конца стержня до точки излома.
|
x |
l |
|
l |
|
l |
|
|
|
|
|
3 |
|
|
|
|
|
||||
|
|
|
|
|
|
2 |
|
|||
|
|
|
P( A) |
3 |
|
3 |
|
|
||
|
|
, |
|
. |
||||||
|
|
|
|
|||||||
|
|
|
|
|
||||||
|
|
|
l |
|
3 |
|||||
|
2l |
|
|
|
|
|
||||
x |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
3 |
|
|
|
|
|
|
|
до ближайшей прямой
составленный иглой с этой
задаёт положение иглы с прямой.
y 2l cos – игла пересекает
2 . З а д а ч а Б ю ф ф о н а .
Плоскость расчерчена па-раллельными прямыми, расстоя-ние между которыми равно a. На плоскость наудачу брошена игла длины l (l<a). Найти вероятность того, что игла пересечет какую-либо прямую.
Решение.
Пусть y – расстояние от центра иглы
|
|
a |
|
|
|
|
0 y |
|
|
, а |
x |
|
– ост-рый угол, |
|
|
|
||||
|
2 |
|
|
|
|
|
прямой |
|
|
|
|
. Пара чисел (x, y) |
|
0 x |
|
|
||||
|
|
|
2 |
|
|
|
точностью |
до |
выбора конкретной |
||||
прямую.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
l |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
cos dx |
|
|
l |
sin x | |
2 |
|
|
|
||||
2 |
|
|
2l |
|
||||||||||
P( A) |
|
2 |
|
|
|
|||||||||
0 |
|
|
|
|
|
0 |
. |
|||||||
|
|
a |
|
|
a |
|
|
|||||||
|
|
|
|
|
|
|
|
a |
||||||
|
|
|
4 |
|
|
|
|
|
4 |
|
|
|
|
|

Глава 2. Условные вероятности; независимость
§ 1. Условные вероятности; теорема умножения
N – число испытаний; |
|
|
|
|
|
|||||||
A, B, AB – события; |
|
|
|
|
|
|
||||||
N(A), N(B), N(AB) – частоты событий; |
|
|||||||||||
|
N ( AB) |
– условная относительная частота события A при условии, что произошло событие B; |
||||||||||
|
N (B) |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
N ( A) |
P( A) ; |
N (B) |
P(B) ; |
N ( AB) |
P( AB) |
||||||
|
|
|
|
|
||||||||
|
N |
|
|
|
N |
|
|
|
N |
|
||
|
|
|
|
|
N ( AB) |
|
|
|
|
|
|
|
|
N ( AB) |
|
N |
|
|
P( AB) |
. |
|
|
|||
|
|
|
|
|
|
|
|
|
||||
|
N (B) |
N (B) |
|
P(B) |
|
|
||||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
N |
|
|
|
|
|
|
|
Если все относительные частоты событий устойчивы, тогда условная относительная частота тоже устойчива.
Пусть P(B)>0.
Условной вероятностью P(A|B) события A при условии, что событие B произошло, называется отно-
шение P( A | B) |
P( AB) |
. |
|
P(B) |
|||
|
|
P(A|B) = PB(A) (встречается в литературе).
Т е о р е м а у м н о ж е н и я
Если P(A)>0, P(B)>0, а P(A|B), то вероятность произведения
Доказательство:
Доказательство следует из определения.
Пример
P( AB)
P(B) P( A |
B)
.
1 способ. В урне находятся M-белых шаров и N-M-черных шаров. По схеме выборки без возвращения, последовательно выбираются два шара. Найти вероятность того, что оба шара будут белыми.
A = {1 вынутый шар белый}
B = {2 вынутый шар белый}
AB = {оба шара белых}
P( A)
P( AB)
M |
, P(B | A) |
|
N |
||
|
P( A) P(B |
M 1 N 1
A) M (M 1) . N (N 1)

2 способ.
|
2 |
|
P( AB) |
A |
|
M |
||
2 |
||
|
||
|
A |
|
|
N |
M! |
|
|
(M 2)! |
|
|
N! |
||
|
||
(N 2)! |
|
M (M 1) N (N 1)
.
Следствие. |
|
|
Пусть события |
A1,..., AN таковы, что |
|
|
P( A |
... A ) |
|
1 |
n |
Доказательство:
P(A |
... |
1 |
|
P( A ) P |
|
1 |
A |
|
1 |
A |
) 0, |
||
n 1 |
|
|
|
( A ) |
P |
|
|
2 |
|
A A |
|
|
|
1 |
2 |
тогда ( A3 ) ...
|
P |
( A ) |
A |
... A |
n |
1 |
n 1 |
|
.
Доказательство проводится методом математической индукции.
§ 2. Формула полной вероятности
Система событий A1,..., An называется конечным разбиением (разбиением) пространства , если они:
1) |
попарно несовместны, т.е. |
Ai Aj , если i j. |
2) |
A1 A2 ... An . |
|
Тео р ем а (Формула полной вероятности)
|
|
|
|
|
|
|
n |
Если A1,..., An – разбиение и все P(Ai ) 0 |
, то для всех событий B P(B) P( Ai ) P(B | |
||||||
|
|
|
|
|
|
|
i 1 |
Доказательство: |
|
|
|
|
|
|
|
B B B(A ... A ) BA BA ... BA |
|
|
|
||||
1 |
n |
1 |
2 |
n |
|
|
|
|
P(B) P(BA |
... BA ) P(BA ) P(BA ) ... P(BA ) |
|||||
|
|
1 |
|
n |
1 |
2 |
n |
Ai )
.
|
|
|
|
n |
|
|
P( A )P(B |A ) ... P( A )P(B | A ) |
|
P( A ) P(B | A ). |
||||
1 |
1 |
n |
n |
i |
i |
|
|
|
|
|
i 1 |
|
|
Пример.
В урне находятся M-белых шаров и N-M-черных шаров. По схеме выборки без возвращения, последовательно выбираются два шара. Найти вероятность события B={второй вынутый шар белый}.
A = {первый шар белый}
A = {первый шар черный}
Решение
A A =
A + A =
P(B) P( A) P(B | |
A) P( A)P(B | A) |
M (M 1) |
|
(N M ) M |
|
|||||
N (N 1) |
N (N 1) |
|||||||||
|
|
|
|
|
|
|
|
|||
|
M (N 1) |
|
M |
. |
|
|
|
|
|
|
N (N 1) |
N |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||
Пример показывает, что при правильно организованной жеребьевке шансы будут равны.
Лекция № 4
§ 3. Формулы Байеса
Т е о р е м а . Если A1 ,..., An – разбиение и все P Ai 0, P B 0 , тогда имеет место следующая формула:

P A |
| B |
P A P B | A |
,i 1,...,n |
||
|
i |
i |
|||
n |
|
|
|||
i |
|
|
|
|
|
|
|
|
k |
k |
|
|
|
|
P A |
P B | A |
|
k1
До к а з а т е л ь с т в о :
По теореме умножения:
P A B P A P B | |
A |
|
||
i |
|
i |
i |
|
P A B P B P A | B |
|
|||
i |
|
i |
|
|
P A |
| B |
P A P B | A |
||
i |
i |
|
||
i |
|
P B |
|
|
|
|
|
|
|
Формулы Байеса можно интерпретировать следующим образом: назовём Ai – гипотезой, |
||||
тат некоторого эксперимента, a |
P Ai – априорные вероятности, а условные вероятности P Ai |
|||
риорные вероятности (послеопыт-ные вероятности).
а
|
B B
–резуль-
–апосте-
Формулы Байеса позволяют по априорным и условным вероятностям вычислить апостериорные вероятности гипотез.
П р и м е р . Детали, изготовленные цехом завода, попадают к одному из двух контролёров для проверки на стандартность. Вероятность того, что деталь попадёт к первому контролёру – 0,6; ко второму контролёру, соответственно, – 0,4. Вероятность того, что годная деталь будет признана стандартной, для первого контролёра – 0,9; для второго – 0,98. Годная деталь была признана стандартной. Найти вероятность того, что её проверил первый контролёр.

Решение. |
|
|
|
|
A деталь проверил |
первый |
|||
1 |
|
|
|
|
A деталь проверил |
второй |
|||
2 |
|
|
|
|
A A , A A |
|
|||
1 |
2 |
1 |
2 |
|
B годная |
деталь признана |
|||
P A |
| B ? |
|
|
|
1 |
|
|
|
|
стандартно й
P A |
| B |
|
P A P B | A |
|
|
|
||
|
1 |
P A |
1 |
P B | A |
|
|||
1 |
P A |
P B | A |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
2 |
|
2 |
|
|
|
0,6 0,9 |
|
0,58 |
|
|
|
|
|
|
|
|
|
|
|
|||
0,6 0,9 0,4 |
0,98 |
|
|
|
|
|
||
§ 4. Независимость событий
Если события A и B таковы, что P B 0 P A | B
О п р е д е л е н и е . Событие A не зависит от события B, если P A | B P A
Если потребовать условия P A 0 |
, то |
|
|||||
P B | A |
P AB |
|
P B P A | B |
|
P B P A |
P B |
|
P A |
P A |
P A |
|||||
|
|
|
|
||||
Понятие того, что одно событие зависит от другого, симметрично. |
|||||||
З а м е ч а н и е . |
|
|
|
|
|
||
Из теоремы умножения: |
|
|
|
||||
P AB P B P A | B |
|
|
|
||||
P AB P B P A |
|
|
|
||||
Это приводит к определению.
О п р е д е л е н и е . События A и B называются независимыми, если вероятность произведения событий равна произведению вероятностей событий P AB P A P B . Если событие A не зависит от со-
бытия B, то они являются просто независимыми. Если P AB P A P B не выполняется, то события явля-
ются зависимыми.
P AB P A P B – теоретико-вероятностная (статисти-ческая) независимость; её следует отличать от причинной независи-мости реальных явлений. Причинная независимость реальных явлений не устанавливается с помощью этого равенства, а постулируется на основе других внешних соображений. При установлении независимости событий A и B часто используется следующий принцип:
События A и B, реальные прообразы которых являются причинно-независимыми, независимы и в теоре- тико-вероятностном смысле. Этот принцип не является теоремой – он установлен практикой человека, а реальный смысл этого принципа можно связать со свойством устойчивости частот:
N AB |
|
N A |
|
N B |
~ ~ |
|
~ |
|
~ |
N |
|
N |
|
N |
|
|
Из теоретико-вероятностной независимости не следует причинная независимость их реальных прообразов.
П р и м е р . Из колоды в 52 карты случайно вынимается одна карта. A={туз}, B={бубновая масть}, AB={вынут туз бубновой масти}.
Решение.
P AB |
|
1 |
|
|
|
|
|
|
|
|
||
52 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||
P A |
4 |
|
|
1 |
|
|
|
|
|
|||
52 |
13 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||
P B |
13 |
|
|
1 |
|
|
|
|
|
|||
52 |
|
4 |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
||||
P A P B |
|
1 |
|
1 |
|
1 |
P AB |
|||||
13 |
4 |
52 |
||||||||||
|
|
|
|
|
|
|
|
|
||||
События A и B – независимые события в теоретико-вероятностном смысле.
Добавим в колоду джокер:
P AB |
1 |
|
|
|
|
|
|
||
|
|
|
|
|
|
||||
|
53 |
|
|
|
|
|
|||
P A |
4 |
|
|
|
|
|
|
||
53 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
P B |
13 |
|
|
|
|
|
|
||
53 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|||
P A P B |
4 13 |
|
52 |
P AB |
1 |
||||
2 |
2 |
53 |
|||||||
|
|
|
|
|
|
||||
|
|
|
|
53 |
|
53 |
|
||
События A и B – зависимые события в теоретико-вероятностном смысле.
О п р е д е л е н и е .
Независимость событий в совокупности.
События A1, A2 ,..., An называются независимыми, если 1 i1 i2 ... im n , где полняется:
P Ai1 Ai 2 ... Ai m P Ai1 P Ai2 ... P Aim
2
m
n
, то вы-
|
В противном случае — события зависимы. |
|
|
З а м е ч а н и е . |
Из определения независимости событий в совокупности следует, что события любого |
подмножества Aj1 , Aj2 |
,..., Ajk множества A1, A2 ,..., An будут независимы в совокупности. |
|
|
П р и м е р . Имеются 4 числа: 2, 3, 5, 30. Наудачу выбирается одно число. Вероятность этого события – |
|
0,25. |
Ak выбранное |
число делится на k . |
Решение.
P A2 12
P A |
|
1 |
|
||
3 |
|
2 |
|
|
P A5 12
P A |
|
1 |
|
||
30 |
|
4 |
|
|
P A A |
|
1 |
P A A |
|
1 |
P A A |
|
1 |
P A A A |
1 |
|||||||
|
|
|
|
||||||||||||||
2 |
3 |
4 |
|
2 |
5 |
|
|
4 |
3 |
5 |
4 |
2 |
3 |
5 |
4 |
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
P A A |
P A |
P A |
|
|
|
|
|
|
|
|
|
|
|
||||
2 |
3 |
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
||
P A A |
P A |
P A |
|
попарно |
|
независимы |
|
|
|
||||||||
2 |
5 |
2 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
||
P A A |
P A |
P A |
|
|
|
|
|
|
|
|
|
|
|
||||
3 |
5 |
3 |
|
5 |
|
|
|
|
|
|
|
|
|
|
|
||
P
P
A2 A2
P A |
||
|
|
3 |
A A |
|
|
3 |
5 |
|
P A |
|
1 |
|
1 |
|
1 |
|
1 |
|||
|
|
|
|
||||||||
|
|
5 |
|
2 |
|
2 |
|
2 |
|
8 |
|
|
|
|
|
|
|
|
|||||
|
1 |
(в совокупности зависимы). |
|||||||||
4 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
||
Совокупная независимость более сильное свойство, нежели попарная независимость.
Т е о р е м а . Если события |
A1 |
, A2 |
||||||||||||
все различны, вероятность |
P Ai |
Ai |
2 |
... |
||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||
P A |
j |
, A |
j |
,..., A |
j |
|
| A |
, A |
,..., A |
|
|
|
||
|
|
2 |
k |
i |
i |
2 |
i |
m |
|
|||||
|
1 |
|
|
|
1 |
|
|
|
|
|||||
Д о к а з а т е л ь с т в о :
,..., A |
||
|
n |
|
A |
||
im |
|
|
P A |
j |
, |
|
1 |
|
являются независимыми, индексы
0 , тогда: |
|
|
||
A |
j |
,..., A |
j |
|
|
2 |
k |
||
|
|
|
||
i |
,i |
,...,i |
, j |
, j |
,..., j |
1 |
2 |
n |
1 |
2 |
k |
–
Глава III. Случайные величины и законы их распределения
§ 1. Случайные величины и законы их распределения
Пусть (Ω, A, P) – произвольное вероятностное пространство.
О п р е д е л е н и чайной величиной (СВ),
x R : X x
е . Числовая функция если
| X x A (*)
X
X
от элементарного события
называется слу-
К о м м е н т а р и й . Смысл определения состоит в следующем: поскольку не любое подмножество пространства Ω является событием, и все события составляют -алгебру подмножества A, то, естественно,
рассматриваются только такие функции X X , для которых имеет смысл говорить о вероятности попадания X X в достаточно большие числовые множества. Свойство (*) гарантирует, что для любого X неравенство X x есть событие, а, значит, имеет смысл говорить о его вероятности.
З а м е ч а н и е . Если вероятностное пространство (Ω,A,P) является конечным, то случайной величиной называется любая числовая функция от элементарного события.
О п р е д е л е н и е . |
Множество возможных значений случайных величин X называется область значе- |
ний числовой функции X |
. Если это множество является конечным или счетным, то случайная величина |
называется случайной величиной дискретного типа (СВДТ). Если это множество является несчетным, то случайная величина называется случайной величиной непрерывного типа (СВНТ).
Пример 1. СВДТ. Опыт – бросание игральной кости. СВ X – число выпавших очков. Множество значений
– {1, 2, 3, 4, 5, 6}.
Пример 2. СВНТ. Опыт – дважды измеряется емкость конденсатора, с помощью точных приборов. СВ X
– разность между результатами первого и второго измерений.
Лекция № 5
Законом распределения СВ называется любое правило (таблица, функция), позволяющее находить вероятности всевозможных событий, связанных со случайной величиной.
Если случайная величина X имеет данный закон распределения, то мы будем говорить, что она распределена по этому закону (подчинена этому закону распределения).
Наиболее простую форму можно придать закону распределения СВДТ, обычно этот закон задается рядом распределений.
Рядом распределений СВДТ Х называется таблица
X |
x1 |
x2 |
… |
xn |
… |
P |
p1 |
p2 |
… |
pn |
… |
pi P X xi ,
x1 x2 ... xn ...
Так как |
|
X x |
, X |
1 |
|
i |
1 . |
p |
|
i |
|
x |
,... |
2 |
|
– попарно несовместны, и сумма этих событий образует .
С помощью этой таблицы можно найти вероятности любых событий.
|
P X B pi |
|
|
||
|
|
|
x B |
|
|
|
|
|
i |
|
|
|
Пример |
|
|
|
|
|
|
|
|
|
|
X |
|
1 |
3 |
5 |
7 |
P |
|
0,1 |
0,3 |
0,2 |
0,4 |
|
P 3 X 4 0,1 0,3 0,4 |
||||
Часто бывает удобно иметь графическое изображение ряда распределения, так называемый многоугольник ряда распределения.
