Радиус и интервал сходимости степенного ряда.

Из теоремы Абеля следует, что если х₁ - точка сходимости ряда, то ряд сходится абсолютно во всех точках интервала (-|x₁|,|x₁|). Еслих₁ - точка расходимости, то ряд расходится во всех точках интервалов

(-, |х₁ |), (|х₁ |,). Отсюда делаем вывод, что существует такое число R, что на (-R,R) ряд сходится абсолютно, а на (-,-R), (R, +) расходится. Таким образом, справедлива следующая теорема.

Т: Областью сходимости степенного ряда является интервал (-R, R). В каждой точке этого интервала ряд сходится абсолютно, а на интервалах

(-,-R), (R, +) расходится.

Интервал (-R,R) называется интервалом сходимости ряда, а R - его радиусом сходимости. Для некоторых рядов интервал сходимости вырождается в т.(R=0), для других - охватывает всю ось ОХ (R=). При х=R ряд может и сходиться, и расходиться (вопрос решается для каждого конкретного ряда).

Укажем способ определения радиуса сходимости ряда. Рассмотрим ряд из абсолютных величин его членов и применим к нему

признак Даламбера: 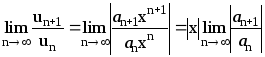. Если<1, т.е. |x|<, то ряд из абсолютных величин членов сходится, и исходный ряд сходится абсолютно. Обозначим

.

При |x|>R степенной ряд расходится, так как общий член ряда a_nxⁿ не стремится к 0. Таким образом, мы получили формулу позволяющую определять радиус сходимости степенного ряда.

Дифференцирование и интегрирование степенных рядов

Т: Пусть функция f(x) является суммой с.р. на (x₀-R,x₀+R). Тогда:

1. f(x) дифференцируема на (x₀-R,x₀+R), причем f(x)=(a₀+a₁(x-x₀)+...+ +a_n(x-x₀)ⁿ +...)=a₁+2a₂(x-x₀)+3a₃(x-x₀)²+...+na_n(x-x₀)^n-1+... сходится абсолютно в этом интервале;

2. f(x) интегрируема на том же интервале, причем для х₁, х₂(x₀-R,x₀+R) имеем

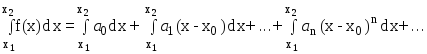
Ряды Тейлора и Маклорена

Пусть функция f(x) в интервале (x₀-R,x₀+R) является суммой степенного ряда:

f(x)=a₀+a₁(x-x₀)+a₂(x-x₀)²+a₃(x-x₀)³+a₄(x-x₀)⁴+...+a_n(x-x₀)ⁿ+...

Коэффициенты могут быть определенны следующим образом:

,... . Тогда имеем:

Полученный ряд называется рядом Тейлора для функции f(x), а в частном случае при х₀=0 - рядом Маклорена:

Таким образом, если функция f(x) разлагается по степеням (x-x0), то этот ряд называется рядом Тейлора и f(x) бесконечно дифференцируема в т. х=х₀.

Необходимое и достаточное условие разложения функции в ряд Тейлора

Пусть функция f(x) бесконечно дифференцируема в т. х=х0. Составим для нее ряд Тейлора. Его сумма не всегда будет совпадать с функцией f(x).

О: Многочленом Тейлора степени n называется частичная сумма

S_n(x)= Остаточным членом ряда Тейлора называется:

R_n(x)=f(x)-S_n(x)

Т: Для того чтобы бесконечно дифференцируемая в т. х₀ функция f(x) являлась суммой составленного для нее ряда Тейлора, необходимо и достаточно, чтобы

Приведем запись остаточного члена в форме Лагранжа

где  находится между х₀ и х.

Разложение основных элементарных функций в ряд Маклорена

Разложение бесконечно дифференцируемой в т. х₀ функции f(x) в ряд Тейлора (в частности Маклорена при х₀=0) распадается на три этапа:

1. Составляется для функции f(x) ряд Тейлора;

2. Находится интервал сходимости ряда;

3. Проверяется, что для составленн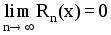ого ряда , т.е.f(x) является суммой этого ряда.

Приведем разложение основных элементарных функций: