
- •Интегральное исчисление функций одной переменной Первообразная и неопределенный интеграл
- •I. Метод замены переменной
- •II. Метод интегрирования по частям
- •Интегрирование специальных классов функций Интегрирование рациональных дробей
- •Интегрирование тригонометрических функций
- •Интегрирование иррациональных функций
- •Определенный интеграл
- •Интегрирование функций нескольких переменных Двойной интеграл
- •Тройной интеграл
- •Комплексные числа и действия над ними
- •Основные понятия о дифференциальных уравнениях
- •Оду 1 порядка. Задача Коши. Общее решение.
- •Дифференциальные уравнения с разделяющимися переменными
- •Однородные ду 1 порядка
- •Линейные оду 1 порядка
- •Линейные ду n-го порядка
- •Понятие числового ряда и его суммы
- •Радиус и интервал сходимости степенного ряда.
- •Дифференцирование и интегрирование степенных рядов
- •Ряды Тейлора и Маклорена
- •Необходимое и достаточное условие разложения функции в ряд Тейлора
- •Разложение основных элементарных функций в ряд Маклорена
- •Применение степенных рядов к приближенным вычислениям
Интегрирование специальных классов функций Интегрирование рациональных дробей
Рациональной
дробью называется функция
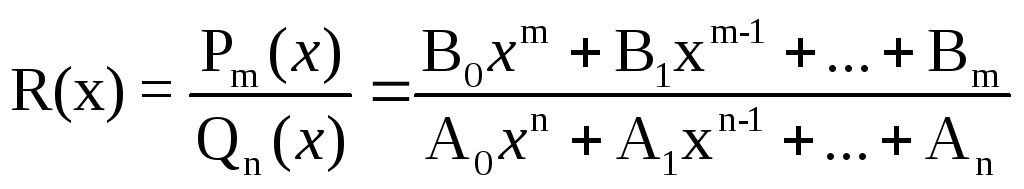 где Bj,
Ai
-заданные коэффициенты,
где Bj,
Ai
-заданные коэффициенты,
![]() ,
,![]() .
Рациональная дробь называется правильной,
если m<n, неправильной, если mn.
.
Рациональная дробь называется правильной,
если m<n, неправильной, если mn.
Всякую неправильную рациональную дробь можно представить в виде суммы многочлена и правильной дроби.
Действительно,
пусть R(x)=![]() - неправильная рациональная дробь.
Разделим числитель на знаменатель,
получим
- неправильная рациональная дробь.
Разделим числитель на знаменатель,
получим![]() ,
где Ll(x)
и остаток rk(x)
- многочлены, а
,
где Ll(x)
и остаток rk(x)
- многочлены, а
![]() - правильная рациональная дробь.
- правильная рациональная дробь.
Любой многочлен
![]() может быть представлен в виде:
может быть представлен в виде:
![]()
Где
![]() - корень кратностиk1;
- корень кратностиk1;
![]() - корень кратностиk2;
- корень кратностиk2;
![]() - корень кратностиkl.
- корень кратностиkl.
В таком случае
правильную дробь
![]() можно представить в виде:
можно представить в виде:
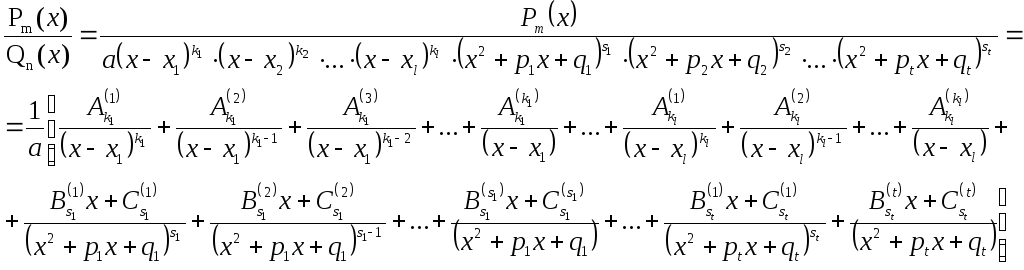
Все дроби представленные в разложении исходной дробно-рациональной функции называются простейшими, числа A, B, C с различными индексами называются неопределенными коэффициентами и однозначно определяются из решения системы линейных уравнений составляемой путем приведения всех простейших дробей к одному знаменателю из соображения однозначности представления многочлена по степеням своей переменной.
В результате представленного разложения становиться возможным вместо взятия интеграла от исходной дробно-рациональной функции (сообразуясь со свойствами неопределенного интеграла) брать интегралы от полученных простейших дробей и в качестве ответа к исходному примеру записывать их линейную комбинацию.
Отметим тот факт,
что получившиеся при разложении
простейшие дроби бывают четырех видов:
![]() ;
;![]() ;
;![]() ;
;![]() .
.
Приведем вычисление интегралов от этих простейших дробей.
1. ![]() .
.
2. ![]() .
.
3. 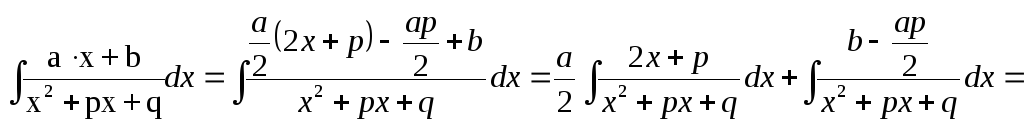
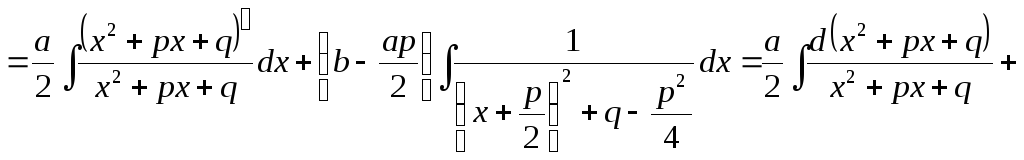
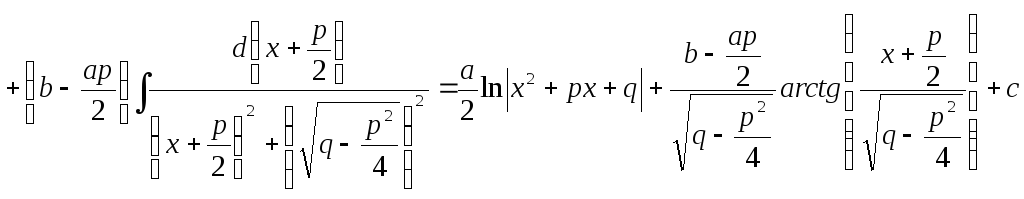
4. 
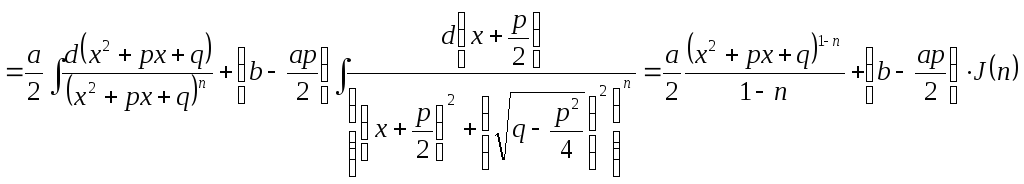
где
![]()
Использовав для
данного интеграла метод интегрирования
по частям можно получить рекуррентную
формулу:
![]() по которой, действуя последовательно,
можно спуститься до
по которой, действуя последовательно,
можно спуститься до![]() .
.
Таким образом, обобщая все вышесказанное можно сформулировать алгоритм пригодный для интегрирования дробно-рациональных функций.
1. Выделяем целую часть, и получаем интеграл от многочлена и правильной дробно-рациональной функции.
2. Представляем правильную дробно-рациональную функцию как сумму простейших дробей.
3. Вычисляем интегралы от простейших дробей.
4. Записываем ответ как сумму от получившихся в п.3. выражений.
Интегрирование тригонометрических функций
Существует несколько подходов к вычислению интегралов от функций содержащих тригонометрические выражения.
1. Интегралы вида
![]() где m и n целые числа и одно из них не
четное вычисляются следующим образом:
где m и n целые числа и одно из них не
четное вычисляются следующим образом:
От простейшей
тригонометрической функции
![]() или
или![]() которая представлена в нечетной степени
отщепляется один сомножитель и заносится
под знак дифференциала, оставшаяся
простейшая тригонометрическая функция
при помощи тождества
которая представлена в нечетной степени
отщепляется один сомножитель и заносится
под знак дифференциала, оставшаяся
простейшая тригонометрическая функция
при помощи тождества![]() преобразуется в дополнительную к себе
функцию, данное преобразование позволяет
передти к табличному интегралу.
преобразуется в дополнительную к себе
функцию, данное преобразование позволяет
передти к табличному интегралу.
2. Интегралы вида
![]() где m и n целые четные числа можно вычислять
посредством применения формул понижения
порядка и перехода к двойному аргументу:
где m и n целые четные числа можно вычислять
посредством применения формул понижения
порядка и перехода к двойному аргументу:
![]() ;
;
![]() ;
;![]()
3. Для интегрирования произведений простейших тригонометрических функций с различными аргументами могут применяться формулы:
![]() ;
;
![]() ;
;
![]()
4. В общем случае
интегралы вида
![]() при помощи замены
при помощи замены![]() ,
при которой
,
при которой![]() ,
,![]() ,
,![]() преобразуются в интегралы отдробно-рациональных
функций, вычисление которых было
рассмотрено выше (обратная подстановка
в этом случае
преобразуются в интегралы отдробно-рациональных
функций, вычисление которых было
рассмотрено выше (обратная подстановка
в этом случае
![]() ).
).
