Линейные оду 1 порядка

О: Линейным ОДУ 1 порядка называется уравнение, линейное относительно неизвестной функции и ее производной:

y+P(x)y=Q(x),

где p(x) и q(x) - заданные непрерывные функции от х или постоянные

Решение такого уравнения находится по формуле:

Линейные ду n-го порядка

О: ОДУ n-го порядка называется линейным, если оно линейно относительно искомой функции и всех ее производных:

a₀(x)y⁽ⁿ⁾+a₁(x)y^(n-1)+...+a_n-1(x)y+a_n(x)y=b(x),

где a_i(x), i=0,n, b(x) непрерывны на некотором интервале (,). Если b(x)0, то называется линейным однородным, в противном случае линейным неоднородным уравнением

Общее решение ЛОДУ n-го порядка имеет вид

y=c₁y₁+ c₂y₂+...+ c_ny_n,

где c_i, - произвольные постоянные, а y₁(х),y₂(х),...y_n(х) образуют фундаментальную систему решений.

Общий вид линейного однородного дифференциального уравнения n-го порядка с постоянными коэффициентами имеет вид:

y⁽ⁿ⁾+a₁y^(n-1)+...+a_n-1y+a_ny=0

где a_i – действительные постоянные.

Уравнение:

λⁿ+a₁λ^n-1+...+a_n-1λ+a_n=0

полученное заменой производных y⁽ⁱ⁾ искомой функции степенями λⁱ называется характеристическим уравнением.

Каждому действительному корню λ кратности r соответствуют r линейно независимых решений исходного уравнения.

, ,…,

Каждой паре комплексных корней кратностиs соответствуют s пар линейно независимых решений.

, ,…,

, ,…,

Таким образом, общее решение линейного однородного дифференциального уравнения n-го порядка с постоянными коэффициентами является линейной комбинацией всех линейно независимых решений.

Общий вид линейного не однородного дифференциального уравнения n-го порядка с постоянными коэффициентами имеет вид:

y⁽ⁿ⁾+a₁y^(n-1)+...+a_n-1y+a_ny= f(x)

где a_i – действительные постоянные.

Его решение может быть получено как сумма общего решения однородного уравнения и частного решения неоднородного.

Частное решение неоднородного дифференциального уравнения n-го порядка с постоянными коэффициентами может быть найдено подбором исходя из вида правой части.

Отметим, что мы рассмотрели лишь простейшие методы решения ОДУ.

В тех случаях, когда необходимо решать нелинейные ОДУ, как правило, используют приближенные численные методы, такие как методы Эйлера, Адамса, Рунге-Кутта и т.п.

Понятие числового ряда и его суммы

О: Числовым рядом называется выражение, полученное последовательным сложением членов числовой последовательности ,..., т.е.

,... . n-ой частичной суммой ряда называется . Ряд называется сходящимся, если существует конечный предел, являющийся суммой ряда; расходящимся, если limS_n= или не существует.

Числа ,...- члены ряда, u_n-n-й или общий член. Коротко ряд записывают

Ряд называется гармоническим рядом и расходится.

Основные свойства сходящихся числовых рядов

1⁰. Отбрасывание конечного числа членов не влияет на сходимость ч.р.

2⁰. Если ряд сходится и имеет сумму S, то ряд, c=const, сходится и имеет сумму cS.

3⁰. Если ряды ,сходятся и имеют суммы S и, соответственно, то ряд сходится и имеет сумму S+.

Необходимый признак сходимости числового ряда

Т: Если ряд сходится , то

Следствие: Если , то рядрасходится.

Необходимый признак не является достаточным. Например, для гармонического ряда , а ряд расходится.

Достаточные признаки сходимости знакоположительных рядов

Т.: (Признак сравнения 1). Пусть для рядов выполняется неравенство:n=1,2,... Тогда :

1.-сходится- сходится;

2.-расходится- расходится

Т.: (Признак сравнения 2). Если для с неотрицательными членами, то оба ряда или сходятся, или расходятся.

Признак Даламбера

Т

<1 ч.р. сходится

>1 ч.р. расходится

=1 сомнительный случай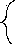

: Если для знакоположительного ч.р.

Интегральный признак Коши

Т

: Пусть члены знакоположительного ч. р. являются при n=1, 2, 3, ... значениями некоторой функции f(x), положительной, непрерывной, монотонно убывающей на [1,), т.е. f(1)=u₁, f(2)=u₂, ..., f(n)=u(n), .... Тогда

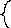сходится ч.р. сходится

расходится ч.р. расходится

Знакочередующиеся числовые ряды. Признак Лейбница

О: Знакочередующимся числовым рядом называется ряд

Т: (Признак Лейбница). Если для ряда выполняются условия:

1. u₁>u₂>...>u_n>...,

2. , то этот ряд сходится, причем его сумма S>0 и S<u₁

Знакопеременные ряды. Абсолютная и условная сходимости

О: Знакопеременным числовым рядом называется ряд , который содержит как положительные, так и отрицательные члены

Знакочередующийся ч.р. является частным случаем знакопеременного ч.р.

Т: (Признак абсолютной сходимости). Если для знакопеременного ч.р. сходится, составленный из абсолютных величин его членов, то рядсходится

О: Знакопеременный ч.р. называется абсолютно сходящимся, если сходится ряди условно сходящимся, если он сходится, хотя рядрасходится

Понятие функционального (ф.р.) и степенного рядов. Теорема Абеля

О: Функциональным рядом называется ряд u₁(x) + u₂(x) + ...+ u_n(x)+..., члены которого является функциями от х

При фиксированном х=х₀ функциональный ряд становится числовым. Областью сходимости ф.р. называется множество Х всех значений х, для которых он сходится.

В области сходимости Х ф.р. его сумма S(х) является функцией от х.

Важным частным случаем ф.р. является с.р.

О: Степенным рядом называется ф.р. вида

=a₀+a₁(x-x₀)+ a₂(x-x₀)²+...+a_n(x-x₀)ⁿ+..., x₀, a₀, a₁ , ..., a_n, ...R

При х₀=0 получаем ряд по степеням х:

=a₀+a₁x+a₂x²+...+ a_nxⁿ+...

Для того чтобы найти область сходимости с.р., докажем теорему Абеля.

Т: (Абеля) Если степенной ряд сходится при х=х₁ 0, то он абсолютно сходится х: |x|<|x₁|. Если ряд расходится в т. х=х₁ , то он расходится  х: |x|>|x₁|