
- •Интегральное исчисление функций одной переменной Первообразная и неопределенный интеграл
- •I. Метод замены переменной
- •II. Метод интегрирования по частям
- •Интегрирование специальных классов функций Интегрирование рациональных дробей
- •Интегрирование тригонометрических функций
- •Интегрирование иррациональных функций
- •Определенный интеграл
- •Интегрирование функций нескольких переменных Двойной интеграл
- •Тройной интеграл
- •Комплексные числа и действия над ними
- •Основные понятия о дифференциальных уравнениях
- •Оду 1 порядка. Задача Коши. Общее решение.
- •Дифференциальные уравнения с разделяющимися переменными
- •Однородные ду 1 порядка
- •Линейные оду 1 порядка
- •Линейные ду n-го порядка
- •Понятие числового ряда и его суммы
- •Радиус и интервал сходимости степенного ряда.
- •Дифференцирование и интегрирование степенных рядов
- •Ряды Тейлора и Маклорена
- •Необходимое и достаточное условие разложения функции в ряд Тейлора
- •Разложение основных элементарных функций в ряд Маклорена
- •Применение степенных рядов к приближенным вычислениям
Тройной интеграл
Пусть теперь в
трехмерной области
задана произвольная непрерывная функция
![]() .
Разобьем
на n частей, аналогично случаям
рассмотренным выше и составим сумму,:
.
Разобьем
на n частей, аналогично случаям
рассмотренным выше и составим сумму,:
![]() которая
называется трехмерной интегральной
суммой для
которая
называется трехмерной интегральной
суммой для![]() в.
в.
Тройным интегралом
от функции
![]() по области
называется предел интегральных суммы
при условии, что диаметр разбиения (т.е.
длина наибольшей хорды) стремиться к
нулю (0),
если предел существует, конечен и не
зависит от способа разбиения
на части i,
по области
называется предел интегральных суммы
при условии, что диаметр разбиения (т.е.
длина наибольшей хорды) стремиться к
нулю (0),
если предел существует, конечен и не
зависит от способа разбиения
на части i,
![]() ,
и от выбора в них точек Мi.
Обозначение
,
и от выбора в них точек Мi.
Обозначение
![]() где dv
- элемент объема;
- область интегрирования;
где dv
- элемент объема;
- область интегрирования;
![]() - подинтегральная функция;
- подинтегральная функция;![]() - подинтегральное выражение.
- подинтегральное выражение.
Функция, для которой тройной интеграл существует, называется интегрируемой.
Аналогично двойному
интегралу в декартовой системе координат
применяют формулу
![]()
Вычисление тройного интеграла сводится к последовательному вычислению трех определенных интегралов.
Если исходная
область
определяется неравенствами:
![]() ,
,![]() ,
,![]() то справедлива формула:
то справедлива формула: ,
т.е. внешний интеграл изменяется от
точки до точки, средний – от функции до
функции, внутренний – от поверхности
до поверхности.
,
т.е. внешний интеграл изменяется от
точки до точки, средний – от функции до
функции, внутренний – от поверхности
до поверхности.
Свойства тройного интеграла полностью повторяют свойства двойного интеграла.
Что
же касается перехода к новым координатам
при вычислении тройного интеграла, то
по аналогии:
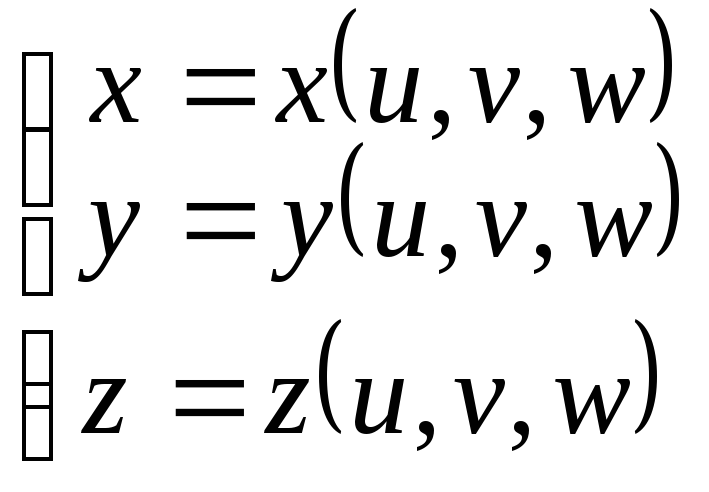 то,
то,
![]() где
где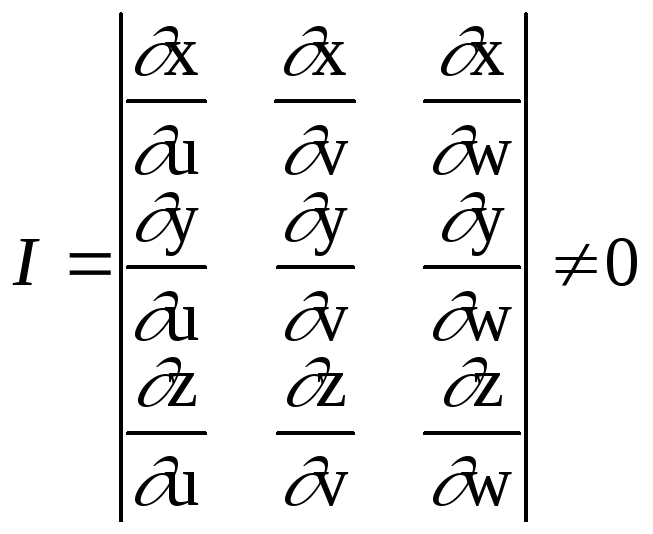 .
.
На практике наиболее распространены переходы к цилиндрическим и сферическим координатам.
Цилиндрические
координаты:
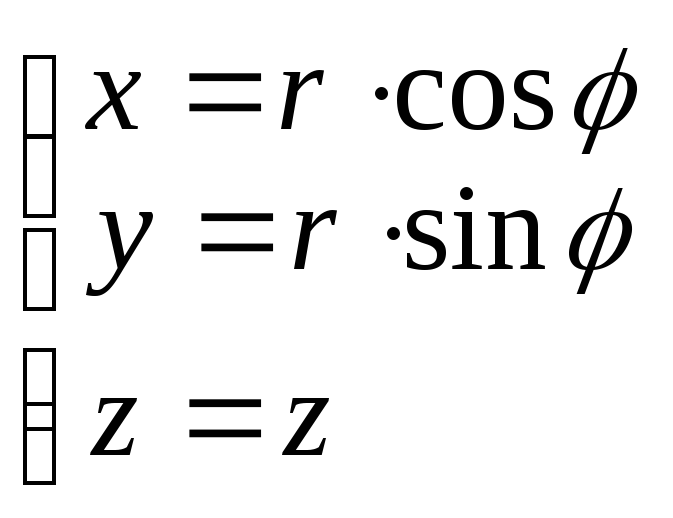 ,
якобиан равен
,
якобиан равен
![]() .
.
Сферические
координаты:
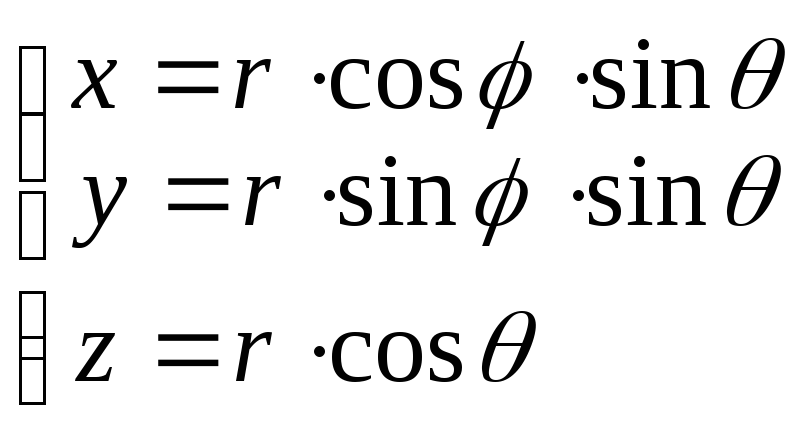 якобиан равенr2sin
якобиан равенr2sin
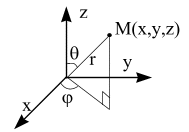
Если говорить о геометрических приложениях тройного интеграла то:
Объем тела ограниченного пространственной областью может быть определен по формуле:
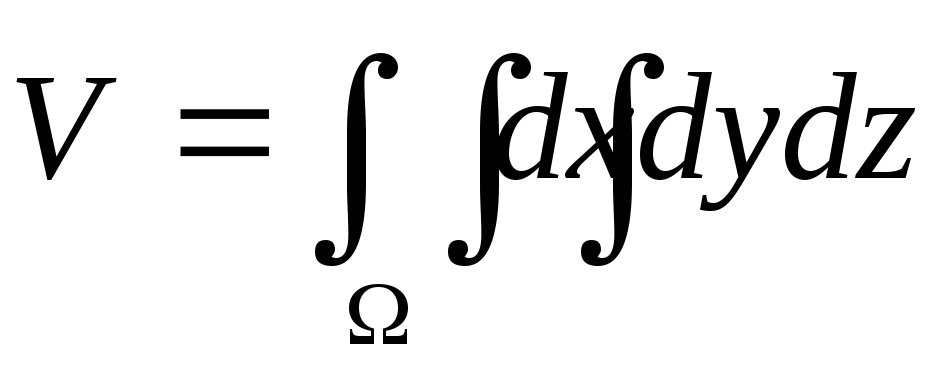 .
.Масса тела в случае если его плотность подчинена закону
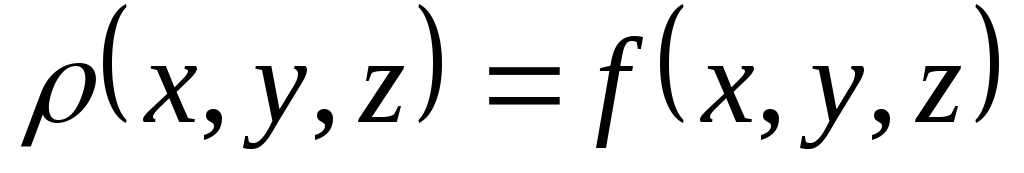 вычисляется по формуле
вычисляется по формуле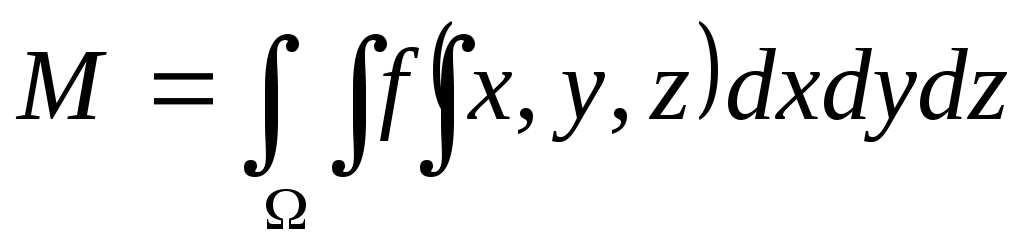 .
.
Комплексные числа и действия над ними
Вводится новое
“понятие” мнимой единицы
![]() (
(![]() ).
С введением этого “числа” появляется
целый класс чисел
).
С введением этого “числа” появляется
целый класс чисел
![]() ,
,
![]() .
Число
.
Число
![]() называется комплексным числом.
называется комплексным числом.
![]() ,
,
![]() - вещественная
и мнимая
его части.
- вещественная
и мнимая
его части.
Над комплексными числами можно производить следующие операции:
Сложение и вычитание:
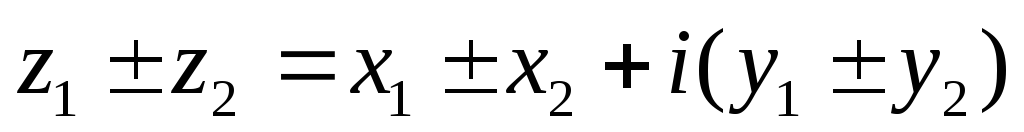
Умножение:
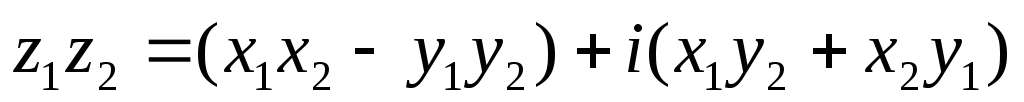
Деление:
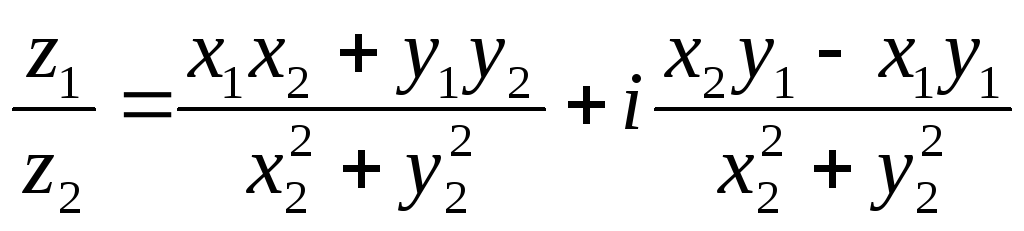
Число
![]() называется
комплексно-сопряженным к числуz:
называется
комплексно-сопряженным к числуz:
если
![]() ,то
,то
![]() .
.
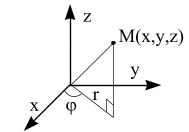
Если вещественные числа можно отображать на прямой, то для комплексных чисел необходима плоскость.
Комплексное число
(это видно из его изображения на плоскости)
можно задавать не только в декартовой
(через
![]() и
и
![]() ),
но и в полярной (через
),
но и в полярной (через
![]() и
и
![]() )
системе координат:
)
системе координат:
![]() - модуль комплексного числа
- модуль комплексного числа
![]() ,
,
![]() - аргумент комплексного числа
- аргумент комплексного числа
![]()
![]() .
.
Значение
![]() выбирается таким образом, чтобы угол
был в той четверти, где находится наше
комплексное число.
выбирается таким образом, чтобы угол
был в той четверти, где находится наше
комплексное число.
Выбранное значение
угла
![]() будем
подчеркивать.
будем
подчеркивать.
 y
y
 r
r

 x
x
Комплексное число
![]() представимо в одной из трех форм записи:
представимо в одной из трех форм записи:
![]() -
алгебраическая форма записи,
-
алгебраическая форма записи,
![]() - тригонометрическая
форма записи,
- тригонометрическая
форма записи,
![]() - показательная
форма записи.
- показательная
форма записи.
Пользоваться тригонометрической и показательной формой удобно в тех случаях, когда нам необходимо разделить или умножить между собой два комплексных числа.
В тригонометрической форме:
если
![]() и
и![]() ,
то
,
то
![]()
![]()
В показательной
форме:
![]() и
и![]() ,
то
,
то![]()
![]()
При работе с комплексными числами часто используются формулы:
Формулы Эйлера: ![]() ;
;
![]()
![]() .
.
Формула Муавра:
![]()
![]()
Корень из комплексного
числа функция многозначная, т. е. одному
значению
![]() соответствуетnзначений функции
соответствуетnзначений функции![]() :
:
![]() k
изменяется от нуля доn-1.
k
изменяется от нуля доn-1.
Область
![]() - это окружность с центром в точке
- это окружность с центром в точке
![]() и радиусомR.
и радиусомR.
