
- •Интегральное исчисление функций одной переменной Первообразная и неопределенный интеграл
- •I. Метод замены переменной
- •II. Метод интегрирования по частям
- •Интегрирование специальных классов функций Интегрирование рациональных дробей
- •Интегрирование тригонометрических функций
- •Интегрирование иррациональных функций
- •Определенный интеграл
- •Интегрирование функций нескольких переменных Двойной интеграл
- •Тройной интеграл
- •Комплексные числа и действия над ними
- •Основные понятия о дифференциальных уравнениях
- •Оду 1 порядка. Задача Коши. Общее решение.
- •Дифференциальные уравнения с разделяющимися переменными
- •Однородные ду 1 порядка
- •Линейные оду 1 порядка
- •Линейные ду n-го порядка
- •Понятие числового ряда и его суммы
- •Радиус и интервал сходимости степенного ряда.
- •Дифференцирование и интегрирование степенных рядов
- •Ряды Тейлора и Маклорена
- •Необходимое и достаточное условие разложения функции в ряд Тейлора
- •Разложение основных элементарных функций в ряд Маклорена
- •Применение степенных рядов к приближенным вычислениям
Интегрирование иррациональных функций
Наибольшую сложность, как правило, представляет интегрирование функций содержащих иррациональную часть. Рассмотрим несколько классов иррациональных функций и приведем стандартные замены применяемые при интегрировании того или иного класса.
1. ![]() замена
замена
![]()
2. ![]() замена
замена
![]()
3. ![]() замена
замена
![]()
Предложенные замены позволяют избавиться от иррациональности в подинтегральном выражении, и вместо вычисления интеграла от иррациональной функции предлагается вычислять интеграл от тригонометрической. Вычисление интеграла от тригонометрической функции рассмотрено ранее.
Интегралы
вида
![]() при помощи выделения полного квадрата
и замены
при помощи выделения полного квадрата
и замены![]() приводятся к одному из трех рассмотренных
типов.
приводятся к одному из трех рассмотренных
типов.
Определенный интеграл
Пусть функция
![]() определенна на отрезке [a,b]
тогда разбив отрезок на n частей точками
a=x0<x1<x2…<xn=b
можно определить так называемую
интегральную сумму,
определенна на отрезке [a,b]
тогда разбив отрезок на n частей точками
a=x0<x1<x2…<xn=b
можно определить так называемую
интегральную сумму,
![]() где точкиi[xi-1,xi]
, а xi=xi-xi-1,
где точкиi[xi-1,xi]
, а xi=xi-xi-1,
![]() .
.
Геометрически
![]() алгебраическая сумма площадей
прямоугольников имеющих основанияxi
и высоты
алгебраическая сумма площадей
прямоугольников имеющих основанияxi
и высоты
![]() смысл
смысл

Определенным интегралом от функции f(x) на [a,b] называется предел ее интегральных сумм при maxxi0, если этот предел существует, конечен и не зависит от способа разбиения [a,b] на отрезки.
Обозначение:
![]()
Числа a и b называют нижним и верхним пределами интегрирования, f(x) - подинтегральной функцией.
Определенный интеграл обладает следующими свойствами:
a) ![]() .
.
b) Если
k=const, то
![]() .
.
c) ![]()
d) ![]()
e) ![]() ,
a<c<b.
,
a<c<b.
f) f(x)(x)
x[a,b]
![]() .
.
g) f(x)
непрерывна
на
[a,b]
[a,b]:
![]() =f()(b-a)
=f()(b-a)
h) f(x)
непрерывна на [a,b]
причем
![]() ,
,![]()
![]()
При вычислении определенного интеграла необходимо сначала вычислить первообразную, после чего воспользоваться формулой Ньютона-Лейбница.
![]()
Отдельно остановимся на геометрических приложениях определенного интеграла.
Площади криволинейной трапеции, боковыми сторонами которой служат прямые x=a и x=b, нижним основанием ось Ox, а верхним основанием график функции
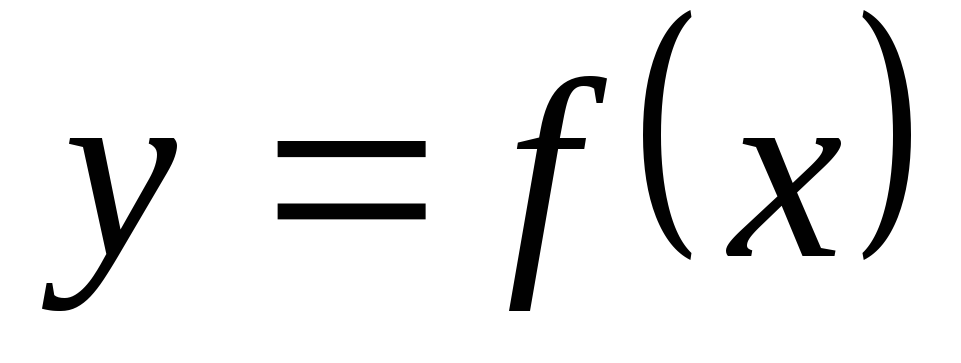 вычисляется по формуле
вычисляется по формуле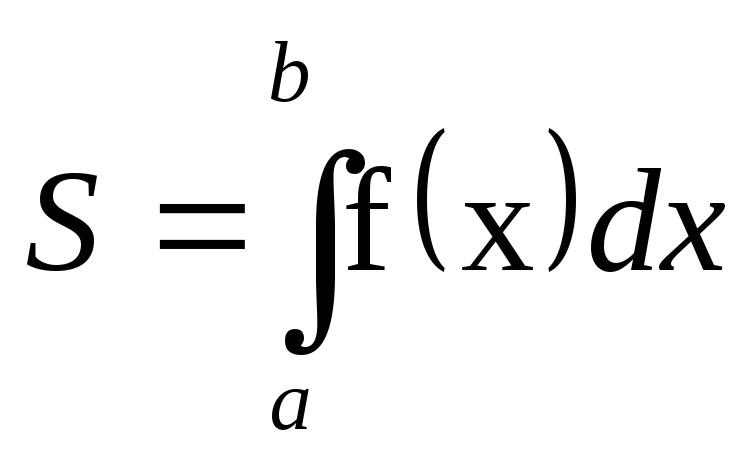 .
.Если гладкая кривая задана уравнением
 то длина ее дуги на отрезке [a,b]
может быть вычислена по формуле:
то длина ее дуги на отрезке [a,b]
может быть вычислена по формуле:
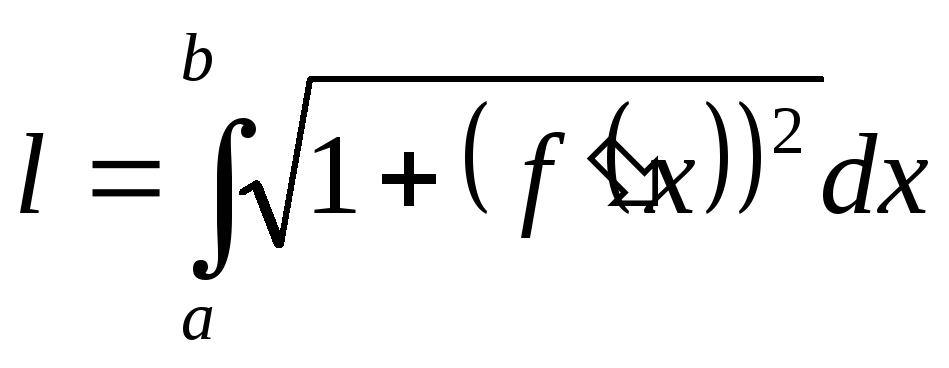 ,
если кривая заданна параметрически
,
если кривая заданна параметрически
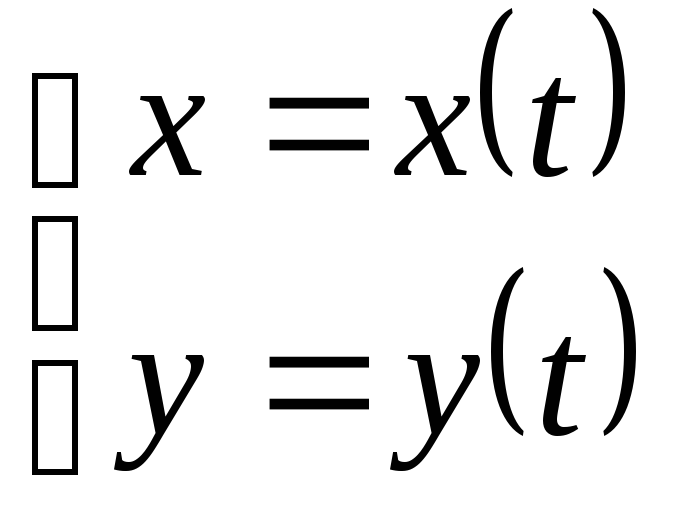
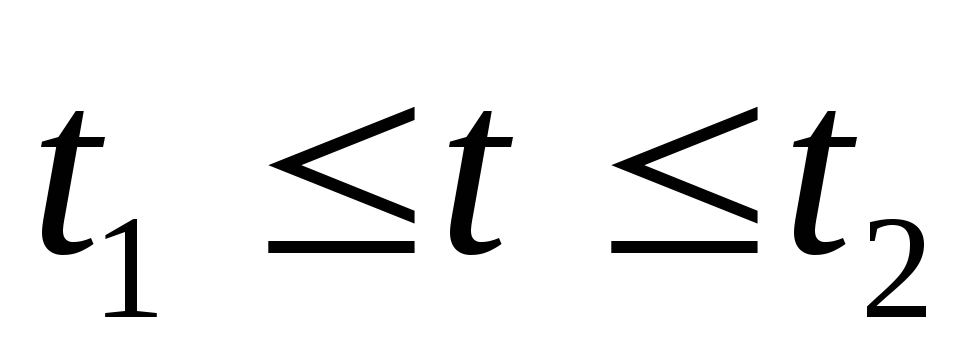 то
то
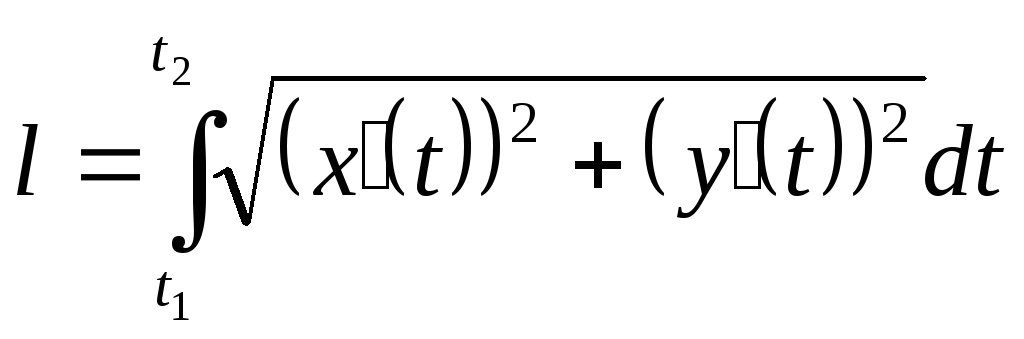 .
.Площадь поверхности образованной вращением вокруг оси Ox дуги кривой заданной уравнением
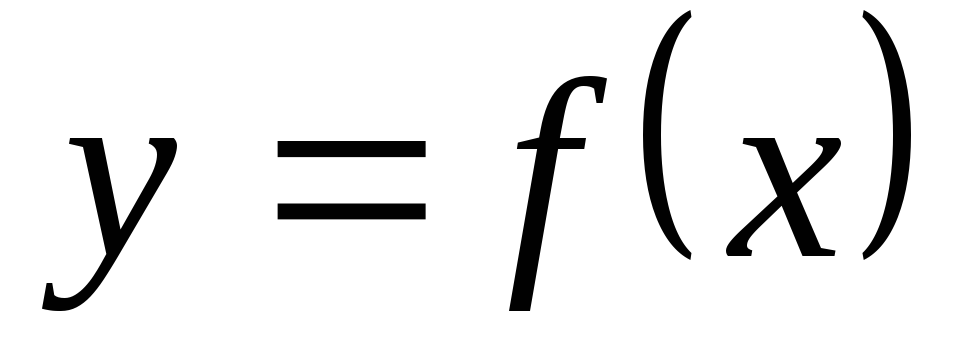
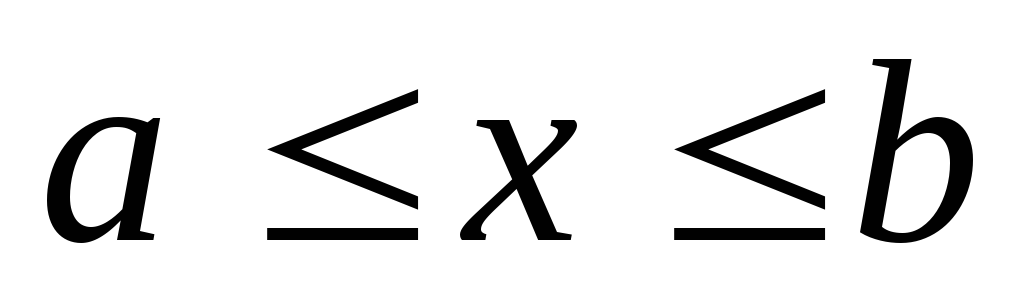 вычисляется по формуле:
вычисляется по формуле:
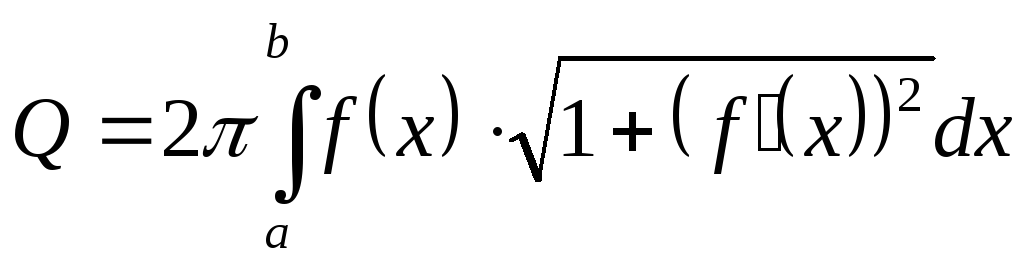 ,
если кривая заданна параметрически
,
если кривая заданна параметрически
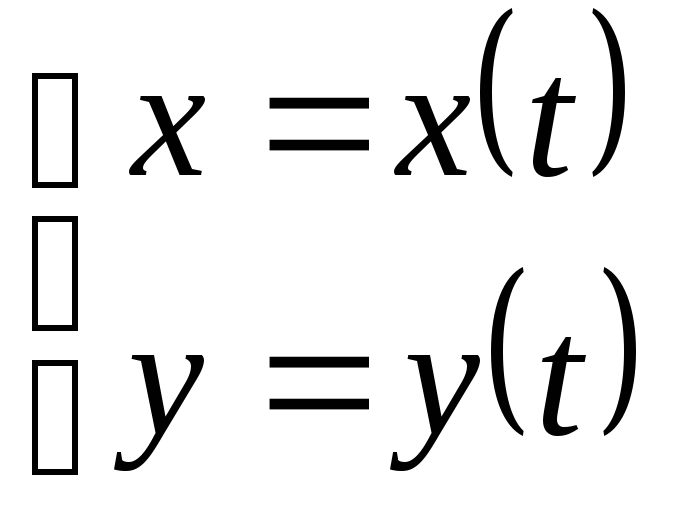
 то
то
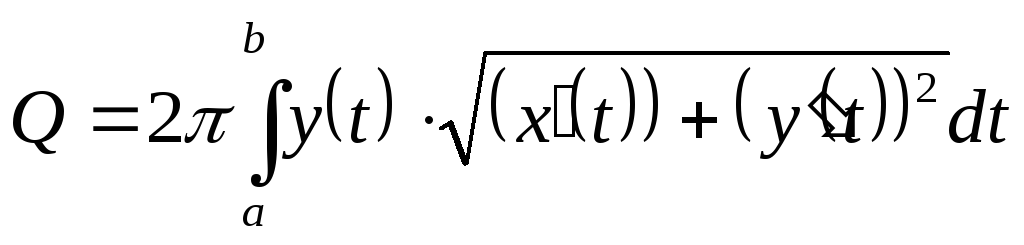 .
.Объем тела вращения дуги вокруг оси Ox определяется как:
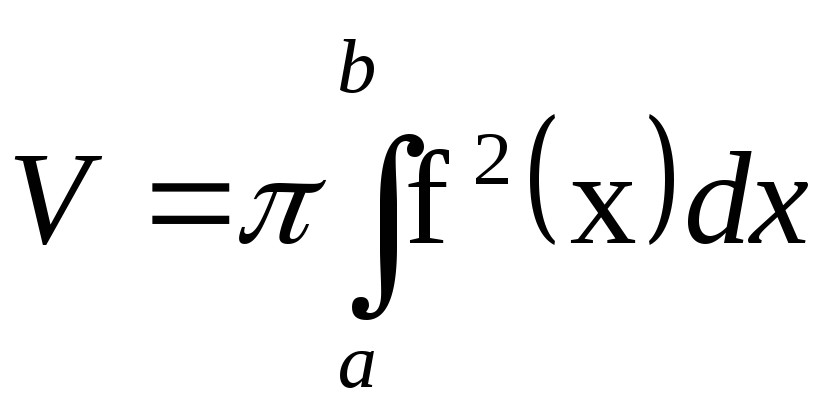 .
.
Интегрирование функций нескольких переменных Двойной интеграл
Пусть
в области D задана функция
![]() .
Разобьем область D на частиDi
с площадями Si,
.
Разобьем область D на частиDi
с площадями Si,
![]() ,
выберем Мi(i,i)
Di
и составим интегральную сумму
,
выберем Мi(i,i)
Di
и составим интегральную сумму
![]()
Двойным интегралом
от функции
![]() по области D называется предел интегральных
суммы при условии, что диаметр разбиения
(т.е. длина наибольшей хорды) стремиться
к нулю (0),
если предел существует, конечен и не
зависит от способа разбиения D на части
Di,
по области D называется предел интегральных
суммы при условии, что диаметр разбиения
(т.е. длина наибольшей хорды) стремиться
к нулю (0),
если предел существует, конечен и не
зависит от способа разбиения D на части
Di,
![]() ,
и от выбора в них точек Мi.
Обозначение
,
и от выбора в них точек Мi.
Обозначение
![]() где ds - элемент площади; D - область
интегрирования;
где ds - элемент площади; D - область
интегрирования;![]() - подинтегральная функция;
- подинтегральная функция;![]() - подинтегральное выражение.
- подинтегральное выражение.
Функция, для которой двойной интеграл существует, называется интегрируемой.
Так
как значение двойного интеграла от
![]() ,
непрерывной вD,
не зависит от вида элементарных частей,
то разобьем D на малые прямоугольники
со сторонами xi
и
yi
прямыми, параллельными осям координат.
При этом
,
непрерывной вD,
не зависит от вида элементарных частей,
то разобьем D на малые прямоугольники
со сторонами xi
и
yi
прямыми, параллельными осям координат.
При этом
![]()
![]() .
Выбирая затем в каждом прямоугольнике
т. Мi(i,i),
можно записать:
.
Выбирая затем в каждом прямоугольнике
т. Мi(i,i),
можно записать:
![]() где ds=dxdy - элемент площади.
где ds=dxdy - элемент площади.
Так как определение двойного интеграла конструктивно аналогично определению определенного интеграла, то двойной интеграл обладает теми же свойствами, что и определенный интеграл.
При вычислении двойной интеграл сводится к повторному по формуле:
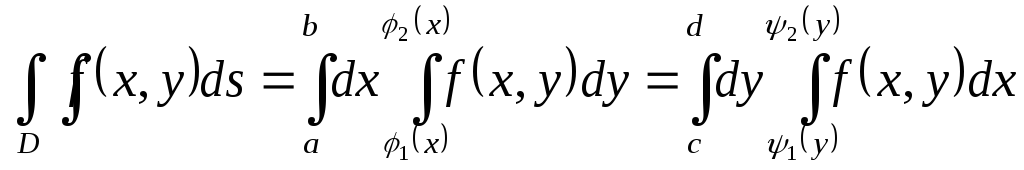
Если граница
области D может быть задана уравнениями:
![]() ,
,![]() (
(![]() ),
x=a,
x=b (a<b),
то двойной интеграл в этом случае
вычисляется по первой части формулы,
причем сначала вычисляется внутренний
интеграл
),
x=a,
x=b (a<b),
то двойной интеграл в этом случае
вычисляется по первой части формулы,
причем сначала вычисляется внутренний
интеграл
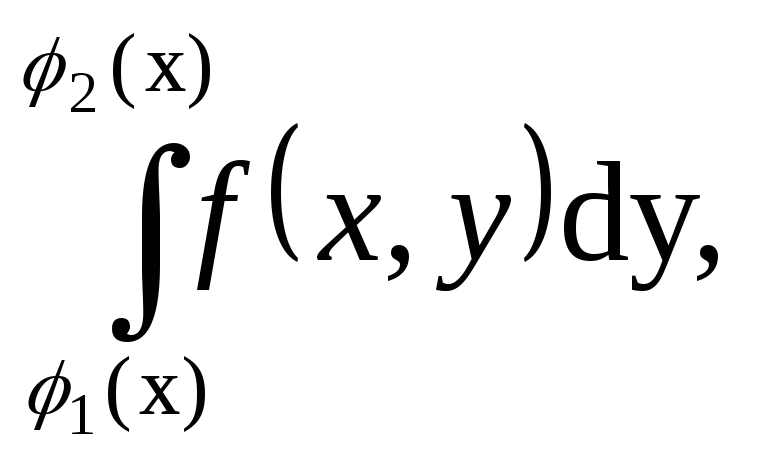 в котором переменная х считается
постоянной, применяя формулу
Ньютона-Лейбница получаем функцию
зависящую только отx,
после чего вычисляется внешний интеграл.
в котором переменная х считается
постоянной, применяя формулу
Ньютона-Лейбница получаем функцию
зависящую только отx,
после чего вычисляется внешний интеграл.
Если граница
области D может быть задана уравнениями:
![]() ,
,![]() (
(![]() ),y=c,
y=d (c<d), то двойной интеграл в этом случае
вычисляется по второй части формулы,
причем сначала вычисляется внутренний
интеграл
),y=c,
y=d (c<d), то двойной интеграл в этом случае
вычисляется по второй части формулы,
причем сначала вычисляется внутренний
интеграл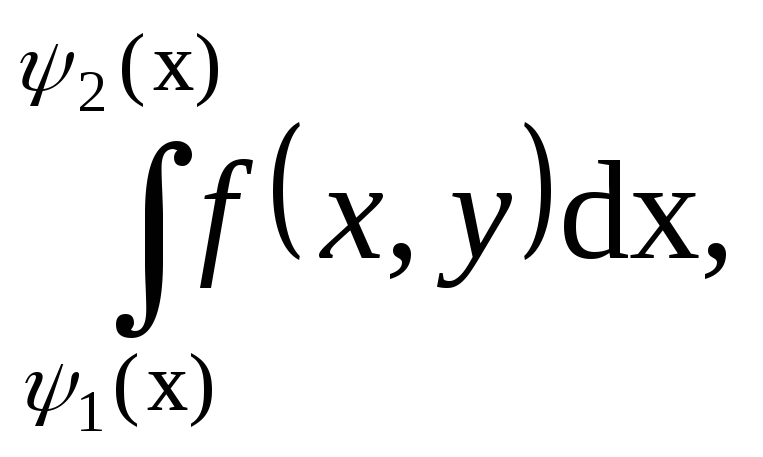 в котором переменнаяy
считается постоянной, применяя формулу
Ньютона-Лейбница получаем функцию
зависящую только от y,
после чего вычисляется внешний интеграл.
в котором переменнаяy
считается постоянной, применяя формулу
Ньютона-Лейбница получаем функцию
зависящую только от y,
после чего вычисляется внешний интеграл.

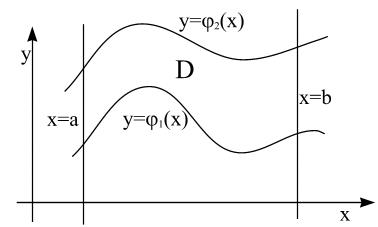
На практике, для определения пределов интегрирования, удобно первым шагом проецировать область на одну из осей, тем самым получая в качестве границ получившегося отрезка пределы внешнего интеграла, после чего двигаясь внутри области по прямым параллельным другой координате определять как граничные функции верхний и нижний пределы внутреннего интеграла. Таким образом внешний интеграл изменяется от точки до точки, внутренний – от функции до функции.
В некоторых случаях для расчетов бывает удобно перейти к новым переменным. Это целесообразно делать в тех случаях, когда уравнения границ области достаточно сложны.
Если в двойном
интеграле
![]() произвести замену переменных:
произвести замену переменных:
![]() то
то
![]() где
где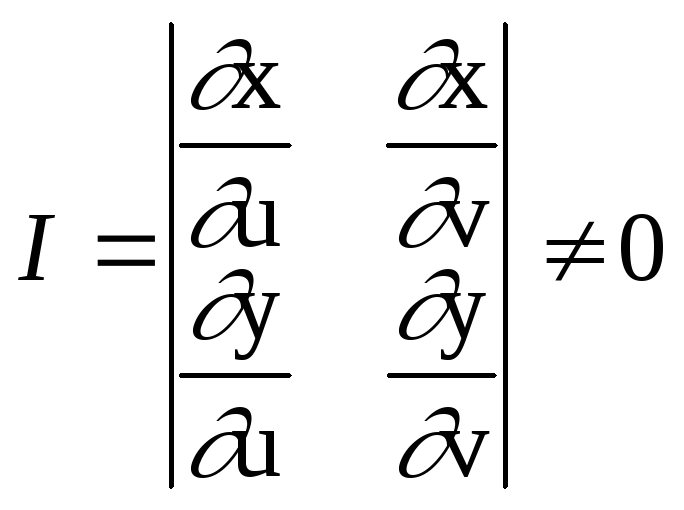 - Якобиан.
- Якобиан.
На практике наиболее
распространен переход к полярным
координатам:
![]() ,
якобиан при этом переходе не сложно
вычислить
,
якобиан при этом переходе не сложно
вычислить
![]() .
.
Если говорить о геометрических приложениях двойного интеграла то:
Площадь плоской фигуры ограниченной областью D, определяется по формуле:
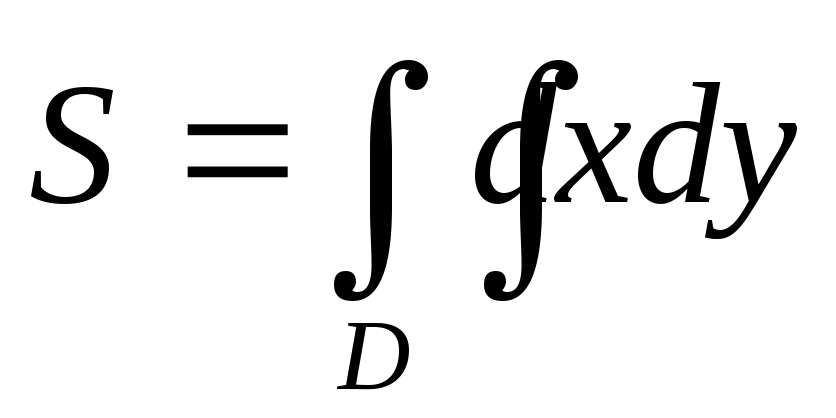 .
.Объем цилиндрического тела ограниченного сверху непрерывной поверхностью
 ,
снизу плоскостью
,
снизу плоскостью ,
с боков цилиндрической поверхностью
вырезающей на плоскости областьD
вычисляется по формуле:
,
с боков цилиндрической поверхностью
вырезающей на плоскости областьD
вычисляется по формуле:
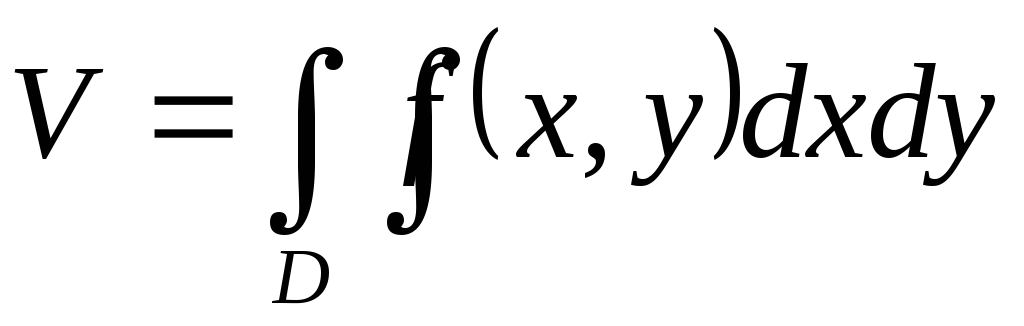
Если гладкая однозначная поверхность задана уравнением
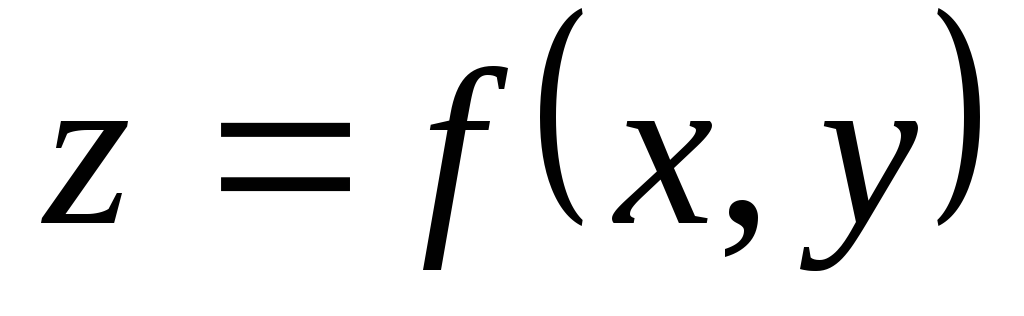 то площадь поверхности выражается
формулой
то площадь поверхности выражается
формулой ,
гдеD–проекция
поверхности на Oxy.
,
гдеD–проекция
поверхности на Oxy.
