Теория игр

Литература

1.Исследование операций в экономике/Под ред. Н.Ш.Кремера. ЮНИТИ,

1997

2.Эддоус, Стэнсфилд. Методы принятия решений.-М.: Аудит, ЮНИТИ,

1997

3.Фомин Г.П. Математические методы и модели в коммерческой деятельности. М.: Финансы и статистика, 2001.

Теория игр

Основные понятия теории игр

Игра-это математическая модель конфликтной ситуации. В отличие от реальных конфликтных ситуаций, в математической модели игра ведется по заранее зафиксированным правилам и условиям.

Ход в игре-это выбор и осуществление одним игроком одного из предусмотренных правилами игры действий. В игре двух лиц ходы строго чередуются. Результат одного хода, как правило, еще не результат игры, а лишь изменение ситуации.

Стратегия-это последовательность всех ходов до окончания игры. Термин партия связан с частичной возможной реализацией правил.

Пусть в игре участвуют n партнеров. Обозначим выигрыш игрока Pj через vj. При этом положительное значение vj означает выигрыш, отрицательноепроигрыш, а нулевое значение-ничья.

Цель игры-максимизация выигрыша за счет другого. Рассмотрим вкратце классификацию игр.

-По количеству игроков игры бывают парные (n=2) и множественные

(n>2).

-В зависимости от числа стратегий игры делятся на конечные, если у игроков имеется конечное число стратегий, и бесконечные, в противном случае.

-Игры бывают с нулевой суммой, если одни выигрывают за счет других.

-Парные игры с нулевой суммой называются антагонистическими.

-Конечные антагонистические игры называются матричными.

-В зависимости от взаимоотношений игроков игры делятся на кооперативные (в которых заранее определены коалиции), коалиционные (игроки могут вступать в соглашения) и бескоалиционные (игрокам нельзя

вступать в соглашения).

Ходы игроков делятся на личные, если ход выбирается сознательно, и случайные, если ход выбирается по механизму случайного выбора.

Стратегии бывают оптимальные, которые обеспечивают игроку наибольший успех-выигрыш, и неоптимальные.

1

Матричные игры

В общем случае матричная игра задается прямоугольной матрицей размерности mxn:

Один игрок имеет m возможных стратегий (A1, A2,…,Am), а другой игрок- n возможных стратегий (B1,B2,…,Bn). Элемент aij R -выигрыш, который платит вто-

рой игрок первому, если первый выбирает стратегию Ai, а второй игрокстратегию Bj. При этом значение выигрыша может быть меньше нуля.

Представим матричную игру в табличной форме, называемой платежной мат-

рицей:

Сформулируем основной принцип матричной игры: первый игрок стре-

мится как можно больше выиграть, а второй – как можно меньше проиг-

рать. Исходя из этого принципа, оба игрока являются сознательными, а матрица игры составлена с точки зрения выигрыша первого игрока; таким образом, выигрыш первого игрока является одновременно проигрышем второго.

Рассмотрим игру с позиции первого игрока. Пусть первый игрок рассматривает возможность применения своей первой стратегии (первой строки матрицы). Тогда его выигрыш в самом худшем случае не будет меньше, чем минимальный

элемент первой строки, т.е. 1 min a1 j . Аналогично, его выигрыш при приме-

j

нении произвольной стратегии Аi составит величину, не меньшую, чем

i min aij . Таким образом, он может среди всех своих стратегий выбрать стра-

j

тегию, наилучшую в смысле наибольшего из возможных минимальных выигрышей. Это значение гарантированного выигрыша в наихудших условиях противодействия второго игрока называется нижней чистой ценой игры, и оно равно следующему выражению (максимину):

max i max minaij

ii j

Теперь рассмотрим точку зрения второго игрока. При использовании им своей первой стратегии, которая представлена первым столбцом платежной матрицы,

его максимальный проигрыш составит величину 1 max ai1 при самых небла-

i

гоприятный действиях первого игрока. Аналогично, его проигрыш при применении произвольной стратегии Вj составит величину, не большую, чем

2

j max aij . Это значение гарантированного проигрыша в наихудших условиях

i

противодействия первого игрока называется верхней чистой ценой игры, и оно равно следующему выражению (минимаксу):

Поэтому стратегии первого игрока называются максиминными, а второго –

минимаксными.

Пример 1. Найти нижнюю и верхнюю чистые цены матричной игры с матрицей:

данном случае a31 v 5. Элемент a31называется седловым элемен-

том матрицы игры (он является одновременно минимальным в своей строке и максимальным в своем столбце), а сама игра – игрой с седловой точкой. При этом нижняя и верхняя чистые цены матричной игры совпадают, и они равны чистой цене игры. Опримальными стратегиями игроков являются A3 , B1, и от-

ступать от них невыгодно ни одному из игроков.

Пример 2. Решим аналогичную задачу для игры с матрицей:

образом, , и в игре отсутствует седловая точка. Решение такой игры затруднено. Поясним эту мысль. Стратегия A2 гарантирует первому игроку выиг-

рыш не менее 4 единиц в худшем случае, когда второй игрок выбирает стратегию B3 . Аналогично стратегия B1 гарантирует второму игроку проигрыш не

более 7 единиц в худшем случае, когда первый игрок выбирает стратегию A1 . Первому игроку можно избрать стратегию A1 , чтобы выиграть 9 единиц, но второй игрок выберет стратегию B2 .

Создается ситуация, когда партнеры заметались по стратегиям. Значит, в данном случае сам подход к игре необходимо менять.

Чистые и смешанные стратегии игроков

Чистая стратегия игрока – это возможный ход игрока, выбранный им с вероятностью, равной 1.

Представим чистые стратегии игроков из примера 1 в виде единичных векторов: стратегия первого игрока A3 : x 0;0;1 , стратегия второго игрока B1 : y 1;0;0 . В общем виде для пары стратегий Ai , B j чистые стратегии можно

3

записать в виде x 0;0;...;1;0;...;0 , y 0;0;...;1;0;...;0 , причем в первом векторе

единица стоит на i-й позиции, а во втором векторе – на j-й позиции. Смешанной стратегией первого (второго) игрока называется вектор:

Здесь величины xi , y j вероятности применения соответствующих стратегий

первого и второго игроков.

Игра называется активной, если xi 0, y j 0 .

Исходя из рассмотренных определений, можно сделать следующие выводы:

1.Игра приобретает случайный характер.

2.Случайной становится величина выигрыша (проигрыша).

3.Средняя величина выигрыша (математическое ожидание выигрыша) яв-

Значение платежной функции при оптимальных стратегиях игроков определяет

Решением игры называется совокупность оптимальных статегий и цены игры. Теорема (основная теорема матричных теории игр - теорема фон Неймана). Любая матричная игра имеет по крайней мере одно решение в смешанных стра-

тегиях – две оптимальные стратегии и соответствующую им цену: 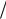x* , y* ,v .

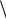Методы решения матричных игр

Все методы решения матричных игр, рассматриваемые в нашем курсе, опираются на теорему об активных стратегиях.

Теорема (об активных стратегиях). Если один игрок придерживается своей оптимальной смешанной стратегии, то выигрыш остается неизменным и равным цене игры, если другой игрок не выходит за пределы своих активных стратегий (т.е. пользуется любой из них в чистом виде или смешивает их в любых пропорциях).

Теперь рассмотрим некоторые частные случаи решаемых матричных игр.

1. Игра, имеющая седловой элемент в платежной матрице (игра с седловой точкой)

4

В этом случае первый игрок реализует свою максиминную стратегию, а второй игрок – свою минимаксную стратегию, нижняя чистая цена игры равна верхней чистой цене игры. Тогда говорят, что игра решается в чистых стратегиях, отклоняться от которых невыгодно никому (см. пример 1).

2. Игра с платежной матрицей 2 на 2, не имеющей седлового элемента.

Здесь нет оптимального решения в чистых стратегиях, поэтому решение отыскивается в смешанных стратегиях. Чтобы их найти, воспользуемся теоремой об активных статегиях. Если первый игрок придерживается своей оптимальной

смешанной стратегии x* , то его средний выигрыш будет равен цене игры v , какой бы активной стратегией ни пользовался второй игрок.

Пусть дана платежная матрица

y1 y2

(вокруг матрицы записаны смешанные стратегии игроков). Запишем для первого игрока два уравнения: первое – для случая прменения вторым игроком только его первой стратегии, и тогда используются только элементы первого столбца матрицы, второе – для случая применения вторым игроком только своей второй стратегии, и тогда используются только элементы второго столбца матрицы. Левые части этих уравнений вычисляют математическое ожидание выигрыша первого игрока, которое равно цене игры. Эти два уравнения содержат сразу три неизвестные - x1, x2 ,v , и сами уравнения при этом являются однород-

ными, поэтому для однозначной разрешимости системы необходимо третье уравнение со свободным членом. Этим добавочным и очень важным уравнением является условие нормировки, согласно которому сумма вероятностей всех событий должна равняться единице. Таким образом, окончательно система уравнений для первого игрока выглядит так:

Эта система решается очень просто по той причине, что в ней можно из третьего уравнения выразить одну неизвестную величину через другую. Решение данной системы дает значения оптимальной смешанной стратегии первого игрока и соответствующую ей цену игры.

Для полного решения игры осталось найти оптимальную смешанную стратегию второго игрока. Здесь игроки как бы меняются местами. Построение системы уравнений аналогично предыдущему случаю. Отличие в том, что в качестве коэффициентов системы берутся не столбцы матрицы, а строки, поскольку именно строки отвечают чистым стратегиям первого игрока. Таким образом, система выглядит так:

5

3.Графическое решение игры два на два.

Снова рассмотрим пример 3. Отложим на оси абсцисс отрезок единичной длины. На концах этого отрезка нарисуем вертикальные оси I-I и II-II. Отложим на

1

оси I-I значения выигрышей первого игрока при использовании им первой стратегии. На оси II-II отложим выигрыши первого игрока при использовании им второй стратегии. Соединим точки отрезками прямых. Ломаная B1 KB2 - нижняя граница выигрыша. На этой границе лежит минимальный выигрыш игрока А при любой его смешанной стратегии. Точка К, в которой этот выигрыш достигает максимума, определяет решение и цену игры. Для смешанной стратегии второго игрока можем также записать:

Стратегию второго игрока можно найти и непосредственно, если на графике поменять игроков местами, а вместо максимума нижней границы выигрыша рассмотреть минимум верхней границы проигрыша. В любом случае точка К является одновременно точкой максимина и минимакса.

4. Графическое решение игры 2 n .

6

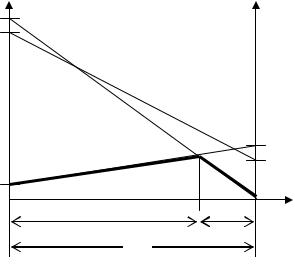
Построение аналогично случаю два на два. Здесь n стратегий противника изобразятся отрезками n прямых. Далее рассматривается нижняя граница, которая представляет собой ломаную. Максимум ломаной достигается в одной из вершин, где пересекаются две стратегии противника, которые являются активны-

ми.

В теории игр доказывается, что у любой конечной игры m n существует решение, в котором число активных стратегий каждой стороны не превосходит наименьшего из чисел m или n . Следовательно, игра 2 n имеет решение, в котором с каждой стороны участвует не более двух активных стратегий. (Так же может быть решена и игра m 2). Стоит только найти эти стратегии – и игра 2 n превращается в игру 2 2 .

Пример 4. Решить игру со следующей платежной матрицей:

B2

В1

K 4 B3

3 В1

1

Эта игра имеет 2 стратегии со стороны первого игрока и три стратегии со стороны второго. Поэтому графическим способом определим одну из стратегий второго игрока, которая является неактивной. Построим график относительно стратегий первого игрока.

Из графика видно, что для второго игрока явно невыгодной является первая стратегия, которая является неактивной. Таким образом, из матрицы игры исключаем первый столбец, соответствующий первой стратегии второго игрока, и приходим к матрице размерности два на два следующего вида:

7

5.Игра с платежной матрицей mx2

Как уже отмечалось выше, игра предварительно решается графически с точки зрения второго игрока. При этом определяются активные стратегии второго игрока. На графике применяется минимаксная стратегия, и рассматривается минимум верхней границы проигрыша. Рассмотрим пример.

Пример. Решить матричную игру со следующей матрицей:

рого игрока при использовании им первой стратегии, а справа – значения проигрышей второго игрока при использовании им второй стратегии.

A3 8

Из графика видно, что вторая стратегия для первого игрока является невыгодной, поскольку при еѐ применении выигрыш первого игрока (и, соответственно, проигрыш второго) будет меньше. Таким образом, активными стратегиями первого игрока будут первая и третья. Соответственно запишем системы уравнений для смешанных стратегий игроков:

8

6.Игры с доминирующими и дублирующими стратегиями.

Рассмотрим две стратегии первого игрока – i – ю и k – ю. При этом пусть для всех элементов соответствующих строк матрицы выполняются условия:

ai1 ak1, ai2 ak 2 , , ain akn.. В этом случае говорят, что i – я стратегия первого игрока доминирует над его j – й стратегией. Если каждое неравенство выполняется как строгое, то говорят, что одна стратегия строго доминирует над другой. В любом случае из двух стратегий первый игрок предпочтет доминирующую, поскольку при использовании доминируемой стратегии его выиг-

рыш по меньшей мере не увеличится. В этом случае можно принять xk* 0 .

Аналогично рассмотрим две стратегии второго игрока - j - ю и l – ю, и при этом для элементов соответствующих столбцов матрицы выполняются условия:

a1 j a1l , a2 j a2l , , amj aml . Для второго игрока, как известно, более выгодной является стратегия, дающая меньший проигрыш, поэтому говорят, что j - я стратегия доминирует над l - й. Если попарные неравенства являются строгими, то говорят, что одна стратегия строго доминирует над другой. При этом, естественно, yl* 0.

Вслучае, если у какого – либо из игроков две стратегии имеют в матрице только совпадающие элементы, то эти стратегии называются дублирующими. При этом неважно, какую из них игрок предпочтет для решения игры.

Врезультате при наличии доминирующих и дублирующих стратегий часть стратегий можно не рассматривать, что приведет в ряде случаев к значительному упрощению платежной матрицы.

7.Эквивалентное преобразование платежной матрицы.

Это преобразование применяется для облегчения расчетов, и при этом оптимальные смешанные стратегии игроков не изменяются.

Теорема. Оптимальные смешанные стратегии x*, y* соответственно 1 – го и 2

– го игроков в матричной игре aij m n с ценой v будут оптимальными и в матричной игре b aij c m n с ценой v bv c , где b 0, c R.

9

b=10, C=-6 . Применим преобразование bA+c, тогда получим игру с теми же оп-

Эквивалентность матричной игры паре двойственных ЗЛП.

Рассмотрим матричную игру размером min m, n 2. Сведем еѐ к задаче линейного программирования в общем виде. Имеем:

Будем считать, что aij 0. Это всегда можно сделать по теореме об эквива-

лентном преобразовании платежной матрицы, следовательно, можно считать цену игры положительным числом, v>0.

Для первого игрока имеем систему неравенств (с учетом того, что первый игрок стремится как можно больше выиграть, цена игры для него будет превышать v):

Введем новые переменные делением на цену игры: ti xvi , тогда получим ЗЛП:

10