Федеральное агентство по образованию

Красноярский государственный университет

Т.И. Качаева

МАТРИЧНАЯ АЛГЕБРА

В ЭКОНОМИКЕ

УЧЕБНО – МЕТОДИЧЕСКИЙ КОМПЛЕКС

Красноярск 2006

ББК

К30

Т.И. Качаева

К30 УМК по матричной алгебре в экономике: программа курса, темы семинарских занятий, вопросы к экзамену, сборник задач / Т.И.Качаева; Красноярский государственный университет – Красноярск, 2006. – 50 с. (экспресс- издание)

Одобрено на заседании методического совета экономического факультета Декан Е.Б. Бухарова _____________ 18 сентября 2006 г.

Программа составлена в соответствии с государственным образовательным стандартом высшего профессионального образования

Предназначено для студентов

экономического факультета.

Печатается по решению редакционно-издательского совета Красноярского государственного университета

@ Красноярский

Государственный

Университет, 2006

Содержание:

1. Программа курса

2. Сборник задач:

1. Комплексные числа. Комбинаторика. Бином Ньютона.

2. Многочлены.

Индивидуальное задание №1

3. Матрицы. Определители.

4.Обратная матрица. Ранг матрицы. Линейная зависимость векторов.

Задачи повышенной сложности.

5. Системы линейных уравнений.

Индивидуальное задание №2

6. Собственные векторы и собственные значения матрицы. Линейные пространства.

7. Базис. Матрицы перехода. Процесс ортогонализации.

8. Матрицы операторов. Квадратичные формы.

9. Число и вектор Фробениуса. Продуктивность матриц.

10. Векторы. Скалярное произведение.

11. Векторное и смешанное произведение векторов.

12. Уравнения прямой на плоскости.

13. Уравнение плоскости. Уравнения прямой в пространстве.

14. Кривые второго порядка.

Индивидуальное задание №3

Программа курса

«Матричная алгебра в экономике»

(64 аудиторных часа: 32 аудиторных часа лекции,

32 аудиторных часа практические занятия)

Курс читается для студентов экономических специальностей дневного отделения во втором семестре.

Цель курса: сформировать у студентов представление о роли и месте алгебры в современной математике и науке; умение логически мыслить; оперировать абстрактными математическими объектами; уметь использовать математические понятия и символы для выражения количественных и качественных отношений.

Содержание курса:

ВВЕДЕНИЕ

ЭЛЕМЕНТЫ ВЫСШЕЙ АЛГЕБРЫ

1. МНОЖЕСТВА ЧИСЕЛ

Множества натуральных, целых, рациональных, иррациональных, действительных чисел.

2. МНОЖЕСТВО КОМПЛЕКСНЫХ ЧИСЕЛ

2.1. Алгебраическая форма комплексных чисел. Операции над

комплексными числами в алгебраической форме

(равенство, сложение, вычитание, сопряжение,

умножение, деление). Свойства этих операций.

Геометрический смысл операций сложения и вычитания.

2.2. Тригонометрическая форма комплексных чисел.

Операции над комплексными числами в

тригонометрической форме. Геометрический смысл

операций умножения и деления в тригонометрической

форме.

2.3. Формулы Муавра (извлечение корняn-ой степени из

комплексного числа, возведение комплексного числа в

n-ю степень).

2.4. Формула Эйлера. Показательная форма комплексного

числа.

2. КОМБИНАТОРИКА. БИНОМ НЬЮТОНА

Перестановки, размещения, сочетания. Биномиальная

теорема. Треугольник Паскаля.

2. ПОЛИНОМЫ В КОМПЛЕКСНОЙ И ДЕЙСТВИТЕЛЬНОЙ ОБЛАСТИ

1. Определение полинома (многочлена).

2. Операции над полиномами (равенство, сложение, умножение, деление (с остатком)).

3. Теорема Безу. Схема Горнера.

4. Решение простейших алгебраических уравнений.

5. Основная теорема алгебры и ее следствия.

6. Разложение на линейные множители на множестве комплексных чисел.

7. Разложение на неприводимые множители (линейные и квадратичные (не имеющие действительных корней)) на множестве действительных чисел.

8. Теоремы о свойствах многочленов с действительными коэффициентами.

9. Теорема Виета.

МАТРИЧНАЯ АЛГЕБРА

1. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ

1. Матрицы. Основные определения. Операции над матрицами (сложение, умножение на число, вычитание, умножение матриц, транспонирование, обращение) и свойства этих операций.

2. Определители. Определение определителей второго и третьего порядка. Миноры и алгебраические дополнения элементов определителя. Определение определителейn-го порядка. Свойства определителей (десять свойств). Практический способ вычисления определителейn-го порядка.

3. Существование и единственность обратной матрицы. Формула для нахождения обратнойматрицы.

4. Рангматрицы. Минорыk-го порядка. Определение ранга матрицы. Метод окаймляющих миноров. Метод вычисления ранга с помощью элементарных преобразований. Теорема об элементарных преобразованиях.

1. АРИФМЕТИЧЕСКОЕ ПРОСТРАНСТВО ВЕКТОРОВ

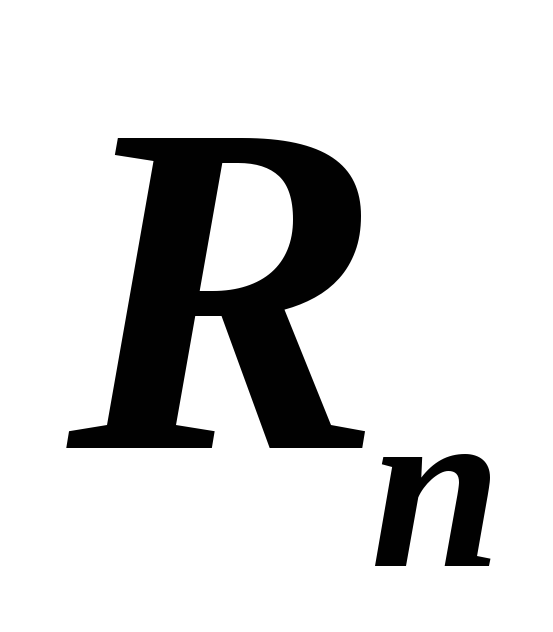
   1. Определение арифметического n-мерного вектора

   2. Операции над векторами (равенство, сумма, произведение вектора на число). Свойства операций (8 аксиом).

   3. Определение арифметического n-го векторного пространства.

   4. Линейная комбинация векторов. Линейная оболочка векторов.

2. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ И НЕЗАВИСИМОСТЬ

ВЕКТОРОВ

1. Определение. Свойства линейной зависимости.

2. Определение максимальной линейно независимой системы векторов.

3. Линейно зависимые и линейно независимые системы в 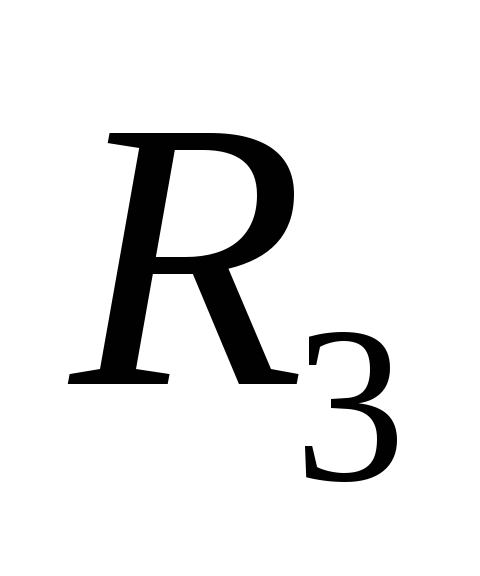. Определение коллинеарности и компланарности векторов.

4. Линейно зависимые и независимые системы в 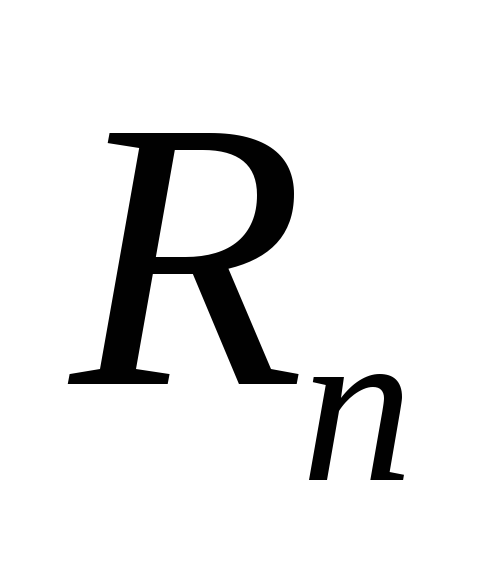. Треугольные системы.

5. Теорема о ранге матрицы (ранг матрицы равен максимальному числу линейно независимых строк и максимальному числу линейно независимых столбцов матрицы).

6. Необходимое и достаточное условие равенства нулю определителя.

1. СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

   1. Определение системы nлинейных уравнений сm

неизвестными.

1. Совместные и несовместные системы.

2. Определенные и неопределенные системы.

3. Однородные системы уравнений.

4. Теорема Кронекера-Капелли.

5. Методы решения систем линейных уравнений: метод Крамера, метод обратной матрицы, метод Гаусса.

6. Решение однородных систем линейных уравнений. Общее решение, частные решения, фундаментальная система решений.

7. Связь между решениями однородной и неоднородной систем линейных уравнений.

1. СОБСТВЕННЫЕ ЧИСЛА И СОБСТВЕННЫЕ ВЕКТОРЫ МАТРИЦЫ

   1. Определение собственного вектора и собственного числа матрицы.

   2. Характеристический многочлен матрицы.

   3. Алгоритм нахождения собственных чисел и собственных векторов матрицы.

2. ЛИНЕЙНЫЕ ПРОСТРАНСТВА

   1. Определение линейного пространства.

   2. Примеры линейных пространств.

   3. Подпространства линейного пространства.

   4. Примеры подпространств.

   5. Базис и размерность линейного пространства.

   6. Примеры базисов в различных пространствах.

   7. Размерность линейного пространства. Теорема о базисе.

   8. Преобразование координат вектора при замене базиса. Матрица перехода от старого базиса к новому.

   9. Ранг и базис системы векторов.

3. ЕВКЛИДОВЫ ПРОСТРАНСТВА.

   1. Определение скалярного произведения векторов.

   2. Определение евклидова пространства .

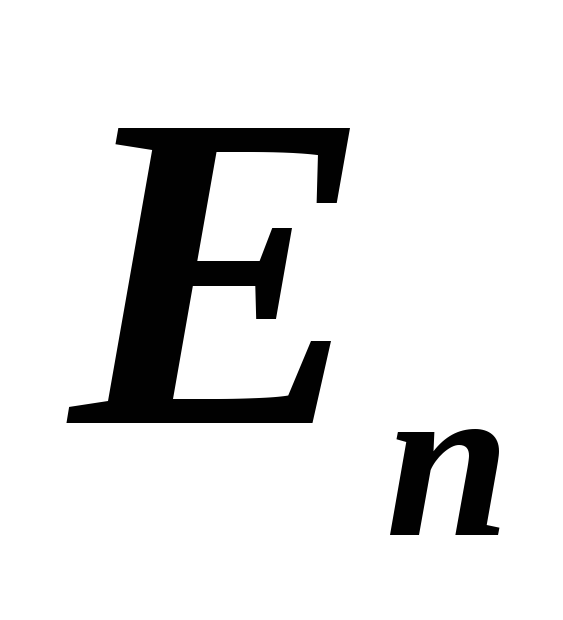   3. Неравенство Коши-Буняковского.

   4. Неравенство треугольника.

   5. Ортогональные системы векторов.

   6. Переход от линейно независимой системы векторов к ортогональной системе векторов (метод ортогонализации Грама-Шмидта).

   7. Ортонормированные системы векторов.

4. ЛИНЕЙНЫЕ ОПЕРАТОРЫ

8.1. Определение линейного оператора.

1. Образ и ядро линейного оператора. Примеры.

2. Матрица линейного оператора. Примеры.

3. Изменение матрицы линейного оператора при переходе к новому базису.

4. Сопряженные и самосопряженные линейные операторы. Их матрицы.

5. Собственные числа и собственные векторы самосопряженного оператора.

6. Теорема о существовании ортонормированного базиса из собственных векторов для самосопряженного оператора.

8. ЛИНЕЙНЫЕ, БИЛИНЕЙНЫЕ И КВАДРАТИЧНЫЕ ФОРМЫ

   1. Определение линейной функции и формы. Примеры.

   2. Определение билинейной функции и формы. Примеры.

   3. Определение квадратичной формы. Примеры.

   4. Преобразования квадратичной формы, матрица квадратичной формы.

   5. Приведение квадратичной формы к каноническому виду.

   6. Закон инерции квадратичных форм.

   7. Положительно определенные квадратичные формы.

   8. Критерий Сильвестра.