области

, то интеграл от этой функции по внешнему

D

контуру, ограничивающему область D, равен сумме ин-

тегралов по всем внутренним контурам, ограничиваю-

щим D, при этом все контуры, как внешний, так и внут-

У

ренние, обходят либо по часовой стрелке, либо против.

Следствие. Если функция ƒ(z) аналитична в некоторойТодно-

связной области D, то для любой дуги L, принадлежащей D, инте-

грал от ƒ(z) по L зависит только от начальной z

0

и конечной

z то-

чек дуги L.

Н

В этом случае пользуются следующим обозначениемБ:

z

й

∫ f (z)dz = ∫ f (ξ)dξ = F(z)− F(z0 ),

L

z0

и

где F(z) – первообразная для ƒ(z), т. е. ƒ(z)= F / (z) .

р

Методы интегрирования не пределенных интегралов для функ-

ции комплексного переменногоотакие же, как и для функции дей-

ствительной переменной. Таблица основных интегралов в обоих

случаях одинакова.

т

и

з

§ 9. ФОРМУЛА КОШИ

Пусть функция ƒ(z) аналитична в замкнутой области

D

и пусть L –

о

граница D. Тогда значения функции ƒ(z) в любой точке z области D

можнопвычислить, зная только значениеƒ(z) на границе L, по следую-

щ йформуле:

е

1

f (ξ)dξ

Р

f (z)=

L∫

,

(19)

2πi

ξ − z

за исключением точки z D . Ограничим точку z окружностью C

радиуса r, взяв r настолько малым, чтобы C не пересекала L (рисУ. 7).

Тогда в замкнутой двусвязной области D* с границей L и C функ-

ция ϕ(ξ) аналитична. По теореме Коши для многосвязнойТобласти

∫

f (ξ)dξ

= ∫

f (ξ)dξ

.

Н

(20)

L

ξ − z

C

ξ − z

Б

й

и

р

Рис. 7

Преобразуем

о

нтеграл, с оящий в правой части (20). Для этого сде-

т

лаем замену переменной: ξ − z = reit (уравнение окружностиC). Тогда

и

it

f (ξ)dξ 2π f (z + reit )

it

2π

it

з

dξ = ire

dt; ∫

=

∫

ire

dt

= i ∫ f (z + re

)dt =

ξ − z

reit

C

0

0

(21)

о

2π

2π

п

2π

)dt

= i ∫

f (z + reit

−i ∫

f (z)dt + i ∫

f (z)dt =

0

0

0

е

= i2∫π[f (z + reit ) − f (z)]dt + 2πif (z).

Р

0

2∫π[f (z + reit ) − f (z)]dt

< 2πε

0

У

lim

2∫π[f (z + reit ) − f (z)]dt = 0.

(22)

r→0 0

Учитывая (22), из выражения (21) имеем следующее:

Н

∫

f (ξ)dξ

= i2∫π[f (z + reit )

− f (z)]dt + 2πif (z).

Т

L

ξ − z

0

Левая часть этого равенства не зависит от r. Переходя к пределу

й

при r → 0 и учитывая (22), получим

f (ξ)dξ

= 2πif (z)

. Формула (19)

L∫

ξ − z

Б

доказана.

и

Пример

С помощью теоремы Коши можно выч слять некоторые контур-

ные интегралы.

оf (z)dz

и

1

ez

= f (4) 2πi = e4 2πi

∫

dz =

∫

(рис. 8).

з

тz − 4

z−5

=2

z −

4

z−5

=2

о

п

е

Р

Пример 2

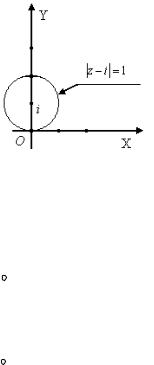
Вычислить

∫

dz

, где С – окружность радиуса 1 с центром в

2

точке i.

C z

+1

У

Решение. Имеем для С уравнение

z −i

=1 (рис. 9).

dz

dz

dz

Н

1

2πi

z +i

=

=

= 2πi

=

= π.

C∫ z2 +1

C∫

(z −i)(z +i)

C∫

z −i

z +i

z=i

2i

Т

Б

й

и

р

интеграл

о

з z2

Рис. 9

тПример 3

Вычислить

, пользуясь формулой Коши:

е

о

L∫

e

dz, L :

z −2

= 3.

z2 −6z

Р

Рпш ние. Воспользуемся интегральной формулой Коши:

1

∫

f (z)dz

= f (z0 ),

где z0 D,

2πi L

z − z0

ez2

ez2

ez2

πi .

∫

dz

= ∫

z −6

dz

= 2πi

= −

L z

2 −6z

L

z

z −6

z=0

3

Обобщая формулу Коши, можно доказать следующую теорему.

У

Теорема. Если функция ƒ(z) аналитична в замкнутой области

D

,

то в каждой точке области D

Т

она дифференцируема

сколько угодно раз, причем n-я производная представ-

ляется формулой

Н

n!

f (ξ)dξ

f (n) (z) =

∫

Б,

(23)

2πi

L (ξ− z)n+1

где L – граница области

й

D обходится в положитель-

ном направлении.

и

Следовательно, из

рсти функции ƒ(z) в некоторой точ-

ке z, т.е. из дифференцируем сти

ƒ(z)

в окрестности этой точки сле-

дует, что ƒ(z) д фференцоруема в точке z сколько угодно раз и, сле-

довательно, все про зводные ƒ(z), ƒ′(z) ,… аналитичны в точке z.

аналитичн

Формула (23) также может служить для вычисления некоторых

контурных интегралови.

з

Пример 4

оezdz

, где L – произвольный замкнутый контур с

Вычислить

п L∫(z −i)3

нтром в точке i.

це

Р

ешение.

ezdz

2πi

(ez )//

∫

=

z=i

= πiei = πi(cos1+i sin1) = π(i cos1−sin1).

L (z −1)3

2!

Пример 5

Вычислить

∫=2

ez

dz.

z

(z −1)(z −3)

Решение.

Т

z

ez

z

e

e

e

z −

3

dz =

dz = 2πi

Н

∫

(z −1)(z −3)

∫

z −1

−3

z=1 = 2πi

−2

= −πУei.

z

=2

z

=2

z

Б

Пример 6

z +1

й

Вычислить

z

∫=2 (z −1)3(z −4)dz.

Решение.

р

z +1

z

о

и

+1