∂u(x, y)

= −

2xy

∂y

(x2 + y2 )2

∂u(x, y)

= −

∂v(x,

y)

.

∂v(x, y)

2xy

∂y

∂x

=

∂x

(x2 + y2 )2

У

Условия выполнены. Функция

f

(z)= 1

Т

является дифференци-

руемой (z ≠ 0).

z

§ 5. АНАЛИТИЧЕСКИЕ ФКП

Введем понятие аналитической функции.

Функция

f (z) однозначная и дифференцируемаяНв каждой точ-

ческой

ке области D называется аналитической (иначе, регулярной или

голоморфной) в этой области.

Б

тической, называются ос быми т

чкамиэтой функции.

Функция

f (z) называется

анал т

в конечной точке z ,

р

если она является аналитической в некоторой окрестности точки z .

Точки плоскости z , в кото ых функц я f (z) не является анали-

о

т

з

Примеры

w = ez – анал т

ческая во всей плоскости;

w = z – нигде не анал т чна.

Убедиться в этомипредоставляем читателю.

f (z) в конеч-

Дифференциалом df (z) аналитической функции

п

∆z

ной т чке z называется главная линейная по отношению к

е

часть риращенияо

∆w этой функции:

Р

′

df (z)= f (z)dz.

Выясним теперь,

любая ли функция двух переменных x и

y

может служить действительной или мнимой частью некоторой ана-

литической функции. Пусть дана функция

f (z)= u(x, y)+iv(x, y)

∂u

=

∂v

;

∂u

= −

∂v .

∂x

∂y

∂y

∂x

Дифференцируем эти равенства соответственно по х и по у:

∂2u ∂2v

∂2u

∂2v

Т

;

,

Н

У

∂x2

=

∂y2

= −

∂y∂x

∂x∂y

так как

∂2v

=

∂2v

,

∂x∂y

∂y∂x

то

∂2u

= −

∂2u

и

∂2u

∂2u

+ Б= 0 .

∂x2

∂y2

и

∂y2

Аналогично получаем, что

р

й

∂2v

∂2v

0.

+

=

∂x

2

∂y

2

т

Видим, что функции u

и v д лжны удовлетворять одному и тому

и

с частными производными вто-

же дифференц альному уравнениюо

называе

∆u =

∂x

2

+

∂y2

= 0.

рого порядка,

мому уравнением Лапласа:

п

∂2u ∂2u

Функция, уд влетворяющая уравнению Лапласа, называется

Две

гармоническойофункцией. Из изложенного следует, что действи-

т льная и мнимая части аналитической функции являются гармо-

Р

нич скими функциями.

На основании условий Коши–Римана

∂u =

∂v

. Отсюда v = ∫

∂udy +ϕ(x).

∂x

∂y

∂x

Т.к.

∂v

= −

∂u

,

то

∂

∂u

dy

+ ϕ'(x) = −

∂u

. Тогда

ϕ'(x) = g(x)

∂x

∂y

∫

∂x

∂x

∂y

и ϕ(x) = ∫g(x)dx +C .

Пример

Построить

аналитическую

функцию,

для

которой функция

u(x, y) = x2 − y2 + 2x

У

является действительной частью (в том, что

Т

функция u(x, y) является гармонической функцией, легко убедиться

проверкой).

∂Нu ∂v

Решение. В силу условий Коши–Римана имеем ∂x =

∂y = 2x + 2 .

Интегрируя

это

равенство

по

y ,

Б

(2x + 2)dy =

v(x, y)=

∫

= 2xy + 2y + ϕ(x). Из равенства

∂v

= −

∂u йполучаем

∂v = 2y +ϕ'(x) = 2y.

∂x

ϕ

=

ϕ

=

∂y

∂x

Отсюда

(x)

0 и

получим

'

(x)

C , где

С – произвольная постоянная.

Тогда

гармоническая

функция, сопряженная с данной, будет

иметь вид

р

о

2y +C.

v(x, y)=

2xy +

т

Искомая анал т ческая функция имеет вид

f (z)

и

2

− y

2

+ 2x + i(2xy + 2y + C)=

= u(x, y)+ iv(x, y)= x

з

.

о

=

(x2 + 2ixy − y2 )+ (2x + 2yi)+ iC =

2

2

+ 2z + Ci.

п

=

(x

+ iy) + 2(x + iy)+ Ci = z

§ 6. ГЕОМЕТРИЧЕСКИЙ СМЫСЛ АРГУМЕНТА И МОДУЛЯ

е

ПРОИЗВОДНОЙ

Р

Пусть функция

w = f (z) аналитична в D,

а

z0 D ;

f '(z0 ) ≠ 0 .

f (z)

отображает

точку

z0

плоскости

Z

в точку

Функция

w0 = f (z0 )

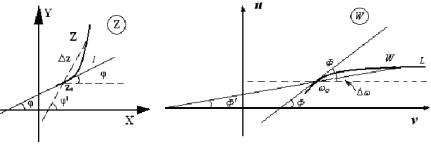
плоскости W (рис. 4).

ски как коэффициент растяжения в точке z0

при отображении

w = f (z) . При этом если

f '(z0 )

>1, то в достаточно малой окрест-

ности точки z0 расстояние между точками

при отображении

w = f (z) увеличивается и происходит собственно растяжение плос-

кости, если же

f '(z0 )

<1 , то отображение приводит к сжатию.

У

Из (13) имеем

: arg

f '(z0 )= α = Ф − ϕ . Отсюда Ф = ϕ + arg f '(z0 ).

Значит, arg f '(z0 ) есть угол, на который нужно повернуть ка-

сательную к кривой l

в точке

z0 для того, чтобы получить

направление касательной к кривой L в точке

w0 .

Т

В силу аналитичности

f (z) в точке z0

Б

α один и

угол поворота

тот же для всех кривых l, проходящих через z0 .

Н

Следовательно, аналитическое отображение обладает свойством

консерватизма

(сохраняемости)

углов

во

всех

точках,

где

f '(z0 ) ≠ 0 . И отображение w = f

и

(z) обладает свойством постоян-

ства растяжения.

р

й

w0 ,

Отображение окрестности точки z0 на окрестность точки

ображение

w =

f (z)

с

f '(z0 ) ≠ 0 ,

осуществляемое аналитическ й функцией

обладает в точке z0

т

св йс в м с хранения углов и постоянством

и

называется конформным отобра-

растяжений. Такое о

жением в точке

z0 .

з

о

п

е

Р