
- •ЛЕКЦИЯ № 1
- •§ 1. Области и их границы
- •§ 3. Элементарные ФКП
- •ЛЕКЦИЯ № 2
- •§ 4. Производная ФКП. Условия Коши – Римана
- •§ 5. Аналитические ФКП
- •ЛЕКЦИЯ № 3
- •§ 7. Интеграл от функции комплексного переменного
- •§ 8. Теорема Коши
- •§ 9. Формула Коши
- •ЛЕКЦИЯ № 4
- •§ 10. Числовые и функциональные ряды ФКП
- •§ 12. Ряд Лорана ФКП
- •ЛЕКЦИЯ № 5
- •§ 13. Особые точки ФКП
- •ЛЕКЦИЯ № 6
- •Практические занятия
- •Ответы
- •ТИПОВОЙ РАСЧЕТ
- •Литература

ЛЕКЦИЯ № 3
§ 7. ИНТЕГРАЛ ОТ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
Важным понятием в теории функции комплексной переменной (КП) является понятие интеграла по комплексной переменной. Метод введения интеграла по КП аналогичен методу введения инте-
грала функции вещественной переменной. |
|
|
|||||||
|
Пусть в области D плоскости z = x +iy задана непрерывная одноУ- |
||||||||
значная функция w = f (z)= u(x, y)+iv(x, y) |
и пусть L – кусочно- |
||||||||
гладкая кривая с началом в z0 и концом в |
|
Т |
|||||||
z , лежащая в области D |
|||||||||
(рис. 5). |
|
|
|
|
|
|
Н |
||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
й |
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
р |
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
и |
|
Рис. 5 |
|
|
|
||
|
|
з |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Задание к нца и начала ориентирует кривуюL. L может быть как за- |
||||||||
мкнутой,отак и незамкнутой. Произвольным образом разбиваем L на n |
|||||||||
«эл м нтарных» дуг в направлении от |
z0 к z точками z1, z2 , , zn−1, |
||||||||
|
п |
|
|
|
|
|
|
|
|
zn = z; zi = xi +iyi . |
|
|
|
|
|
|
|
||
еОбозначим |
|
|
|
|
|
|
|
||
Р |
|
|
|
|
|
|
|
|
|
где ∆xk = xk – xk-1, ∆yk= yk – yk-1;
24
|∆zk| – длина хорды, стягивающей k-ю элементарную дугу. В произвольном месте каждой элементарной дуги (zk-1, zk) возьмем
соответственно по точке χk = ξk + iηk и составим сумму
|
|
|
|
|
|
Sn |
= ∑n |
f (χk ) ∆zk |
|
= ∑n |
f (χk )(zk − zk −1). |
|
|
|
У |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
(14) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
k =1 |
|
|
|
|
|
|
|
|
k =1 |
|
|
|
|
|
|
|
Т |
||||||
Если при max | zk − zk −1 |→ 0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
существует предел сумм (14), не |
||||||||||||||||||||||||||||||||
зависящий ни от способа разбиения кривой L |
|
|
Н |
|
||||||||||||||||||||||||||||
на части, ни от выбора |
||||||||||||||||||||||||||||||||
точек χk |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|||
на всех этих частичных кривых, то этот предел называется |
||||||||||||||||||||||||||||||||
контурным интегралом от функции f(z) вдоль линии L (или ин- |
||||||||||||||||||||||||||||||||
тегралом от функции f(z) по кривой L) и обозначается |
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
й |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
∫ f (z)dz = |
|
|
|
|
и |
(χk )∆zk. . |
|
|
|
|
|
(15) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
lim |
|
|
∑n |
f |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
max ∆zk |
→0 k =1 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
р |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Рассмотрим вопрос о существовании интеграла (15). Представим |
||||||||||||||||||||||||||||||||
суммы (14) в следующем виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
n |
|
|
|
|
|
и |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
∑ |
f (χ |
k |
)(z |
k |
− z |
k −1 |
)= |
|
о(u(ξ ,η |
k |
)+iv(ξ |
k |
,η |
k |
)) (∆x |
k |
+i∆y |
k |
)= |
|
||||||||||||
|
|
|
|
|
|
|
|
∑ |
k |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
k =1 |
|
|
|
зn |
|
|
k =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
= n |
|
[u(ξ |
|
,η ) ∆x |
|
|
−v(ξ ,η ) ∆y ]+ |
|
|
|
|
|
(16) |
||||||||||||||
|
о |
∑ |
|
|
k |
|
|
k |
|
k |
|
|
|
k |
|
k |
|
|
k |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
k =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
е |
|
|
|
|
|
+i |
∑[u(ξk ,ηk ) ∆yk +v(ξk ,ηk ) ∆xk ]. |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
k =1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дпйствительная и мнимая части в равенстве (16) представляют |
||||||||||||||||||||||||||||||||
собой интегральные суммы криволинейных интегралов второго ро- |
||||||||||||||||||||||||||||||||
да. Cледовательно, интеграл (15) существует, если существуют два |
||||||||||||||||||||||||||||||||
криволинейных интеграла |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∫udx −vdy |
|
и ∫udy + vdx . |
|
|
|
|
|
(17) |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
|
25
Но эти два интеграла (17) существуют для непрерывных на L функций u и v. А их непрерывность в нашем случае следует из непрерывности функции f(z). Следовательно, если f(z) непрерывна на L, то интеграл (15) существует и имеет место следующее равенство:
|
|
|
|
∫ f (z)dz = |
∫u(x, y)dx − v(x, |
|
|
|
|
|
У |
|||||
|
|
|
|
y)dy + i∫v(x, y)dx + u(x, y)dy . (18) |
||||||||||||
|
|
|
|
L |
|
|
|
L |
|
|
L |
|
|
Т |
||
|
Из формулы (18) следует, что свойства интеграла (15) аналогич- |
|||||||||||||||
ны свойствам криволинейных интегралов 2-го рода: |
Н |
|
||||||||||||||
|
1) ∫[f1(z)+ f2 (z)]dz = ∫ f1(z)dz + ∫ f2 (z)dz ; |
|
||||||||||||||
|
|
|
|
L |
|
|
|
|
L |
|
L |
|
|
|
||
|
2) ∫аf (z)dz = а∫ f (z)dz ; |
|
|
|
|
|
||||||||||
|
|
|
|
L |
|
|
|
|
L |
|
|
|
Б |
|
||
|
3) ∫ f (z)dz = − ∫ f (z)dz , |
|
|
|
|
|||||||||||
|
|
|
|
L |
|
|
|
|
L− |
|
|
|
|
|||
где |
|
|
|
|
|
|
|
|
|
|
й |
|
|
|
||
|
L− – линия, совпадающая сL, но противоположно направленная; |
|||||||||||||||
|
4) |
|
∫ f (z)dz = ∫ f (z)dz + ∫ f (z)dz . |
|
|
|
|
|
||||||||
|
|
|
|
L1+L2 |
|
|
|
L1 |
L2 |
|
|
|
|
|
|
|
Пусть x = x(t), y = y(t), zжно(t) = x(t) + iy(t) – параметрические урав- |
||||||||||||||||
|
|
|
|
|
|
|
Вычисление контуиных интегралов |
|
|
|||||||
|
Контурные интегралы м |
рвычислять, сводя их с помощью |
||||||||||||||
формулы (18) к двум дейс ви ельным криволинейным интегралам. |
||||||||||||||||
|
|
|
|
|
|
з |
|
|
|
|
|
|
|
|||
нения линии |
|
L; z0т=x(t0)+iy(t0); z=x(t1)+iy(t1). Тогда ∫ f (z)dz = |
||||||||||||||
|
|
|
|
|
о |
и |
|
|
|
|
|
L |
|
|||
t1 |
[u |
|
y |
|
t1 |
[u(x(t), y(t)) y (t)+v(x(t), y(t))× |
||||||||||
= ∫ |
(x(t), y(t)) x (t)−v(x(t), y(t)) |
(t)] dt +i ∫ |
||||||||||||||
|
|
|
п |
|
′ |
|
|
′ |
|
|
|
′ |
|
|||
t0 |
|
|
|
|
|
|
|
t0 |
|
|
|
|
||||
е |
t1 |
|
|
|
|
|
|
|
|
t1 |
f (z(t)) z (t) dt. |
|||||
× x |
(t)]dt = ∫[u(x(t), y(t))+iv(x(t), y(t))][x (t)+iy (t)]dt = |
∫ |
||||||||||||||
Р |
′ |
|
|
|
|
|
|
|
|
′ |
|
′ |
|
|
′ |
|
|
|
|
|
|
t0 |
|
|
|
|
|
|
|
|
t0 |
|
|
|
Эта формула удобна для вычислений контурных интегралов. |
|||||||||||||||
|
|
|
|
|
|
|
|
|
Пример 1 |
|
|
|
|
|
||
|
Вычислить: |
|
∫z dz , где L – отрезок, соединяющий точки z0 = 0; |
|||||||||||||
L
z = 2 + i.
26

Решение. Имеем y = x/2.
∫zdz = ∫(x −iy)(dx +idy)= ∫xdx + ydy +
|
L |
L |
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
2 |
|
xdx |
2 |
|
dx |
|
x |
|
|
5 |
2 |
5 |
|
||
+i∫xdy − ydx = ∫ |
xdx + |
|
|
+i ∫ |
x |
|
− |
|
dx |
= |
|
∫xdx = |
|
. |
||
4 |
2 |
2 |
4 |
2 |
||||||||||||
L |
0 |
|
|
0 |
|
|
|
|
0 |
|
||||||
|
|
Или: x = 2t; y = t . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
||||||||
|
|
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
z = 2t + it = (2 + i)t; dz = (2 + i)dt; |
|
= (2 −i)t ; |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
z |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
∫zdz = ∫1 |
(2 −i)t (2 +i)dt = (4 +1) ∫1 tdt = |
5 . |
|
|
Т |
||||||||||||||||||||||||
|
|
|
|
|
|
L |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 2 |
|
|
|
|
|
|
|
|
|
|
Н |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
∫(1+i − 2z)dz, |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
Вычислить интеграл |
|
где L – дуга параболы от |
|||||||||||||||||||||||||||||||
точки z1 = 0 до z2 =1+i . |
L |
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|||||||||||||||||
|
|
Решение. Преобразуем подынтегральнуюйфункцию 1+i − 2z = |
|||||||||||||||||||||||||||||||||
= (1−2x)+i(1+ 2y), где u(x, y)=1− 2x , |
v(x, y) |
=1+ 2y , т.к. |
∫ f (z)dz = |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
L |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
р(1+i −2 |
|
|
)dz = |
|
|
|
|
|
|
|
|
|
|
||||||
= |
|
|
u dx −vdy +i |
|
v dx +udy, |
|
|
|
|
(1−2x)dx −(1+ 2y)dy + |
|||||||||||||||||||||||||
|
∫ |
∫ |
|
z |
∫ |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
L |
|
(1+ 2y)dx + |
L |
|
−2x)dy. |
|
|
|
|
|
L |
|
|
|
|
|
|
|
L |
|
|
|
|
|
|
|
|
|
||||||
+i∫ |
(1 |
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
L |
|
|
|
|
|
|
то |
|
|
|
(0 ≤ x ≤1). |
|
|
|
|
|
|
|
|||||||||||||||
|
|
Для параболы |
|
y = x2 |
|
dy = 2xdx, |
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
и |
|
|
|
1 |
(1−2x −(1 |
|
|
|
|
|
)2x)dx +i |
1 |
(1 |
|
|
+(1− 2x)2x)× |
|||||||||||
|
|
След |
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
2 |
|
2 |
||||||||||||||||
|
|
|
|
|
|
(1 |
+i − |
2z)= |
∫ |
+ 2x |
∫ |
+ 2x |
|||||||||||||||||||||||
|
|
|
|
|
|
з∫ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
4 |
|
|
|
|
L |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
×dx = −2вательно+ i. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
п |
|
|
|
|
|
§ 8. ТЕОРЕМА КОШИ |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
еассмотрим условие независимости от пути интегрирования L |
|||||||||||||||||||||||||||||||||||
интеграла функции комплексного переменного |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∫ f (z)dz . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
L
Это условие определяется теоремой Коши
27

Теорема Коши. Если функция f(z) аналитична в замкнутой односвязной области D, то интеграл от этой функции по контуру L, ограничивающему область D, равен нулю:
∫ f (z)dz = 0.
L
|
|
|
|
|
|
|
|
Доказательство |
|
|
|
|
У |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проведем в предположении о непрерывности производнойf′(z) в D , |
|||||||||||||||||||
не входящем в определение аналитической функции, |
что значи- |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т |
|||||
тельно упростит рассуждения (теорему можно доказать и без этого |
||||||||||||||||||||
предположения). |
|
|
|
|
|
|
|
|
|
Н |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Доказательство сводится к доказательству равенства нулю двух |
|||||||||||||||||||
действительных криволинейных интегралов |
Б |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
∫udx −vdy |
∫udy + vdx . |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
L |
|
|
|
L |
й |
|
|
|
|
|
|
|
|||
|
На основании условия независимостииот пути интегрирования криво- |
|||||||||||||||||||
линейного интеграла |
∫ |
P(x, y)dx + Q(x, y)dy от функции действитель- |
||||||||||||||||||
|
|
|
|
|
L |
|
|
|
|
р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
∂P ∂Q |
|
|
∂u |
∂v ∂v ∂u |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ного переменного ∂y |
= |
|
∂x |
|
имеем следующее: ∂y = − ∂x ; |
∂y = ∂x . |
||||||||||||||
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
||||
|
Непрерывность же частных производных функции u и v сразу же |
|||||||||||||||||||
вытекает из непрерывностии f(z).Теорема Коши доказана. |
|
|
|
|
|
|
||||||||||||||
|
Сф рмулируем теорему Коши для многосвязной области. |
|
|
|
|
|||||||||||||||
|
|
з |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
ТеоремаоКоши для многосвязной области. Если функция f(z) |
|||||||||||||||||||
|
|
аналитична в замкнутой многосвязной области |
|
, то |
||||||||||||||||
|
|
D |
||||||||||||||||||
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
е |
интеграл от этой функции по границе области D, прохо- |
|||||||||||||||||||
димой в положительном направлении, равен нулю. |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Р |
|
|
|
|
|
|
|
Доказательство |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рассмотрим на примере трехсвязной области (рис. 6). Проведем два разреза γ1 и γ2 ; обозначим через Г сложный замкнутый контур,
28
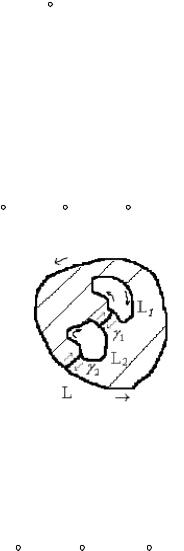
состоящий из контуров L, L1, L2, γ1 , γ2 (причем у каждого разреза
следует различать два берега). Область, ограниченная контуром Г, будет односвязной. В силу теоремы Коши для односвязной области
будем иметь следующее: |
∫ f (z)dz = 0, |
причем контур Г обходится в |
||||||||||
|
|
|
|
|
Γ |
|
|
|
|
|
|
|
таком направлении, при котором областьD остается слева, т.е. в поло- |
||||||||||||
жительном направлении. При этом обходе каждый из разрезов γ1 , |
γ2 |
|||||||||||
будет проходиться дважды в противоположных направлениях, в силу |
||||||||||||
|
|
|
|
|
|
|
|
|
|
Н |
У |
|
чего интегралы по каждому из разрезов взаимно уничтожатся. |
||||||||||||
∫ f (z)dz = ∫ f (z)dz + ∫ |
f (z)dz + ∫ |
f (z)dz + ∫ f (z)Тdz + |
||||||||||
|
|
|
L |
|
|
|
|
L1 |
|
Б |
|
|
Γ |
|
|
|
γ1 |
|
|
|
γ2 |
|
|
||
|
|
+∫ f (z)dz + ∫ |
f (z)dz + ∫ |
f |
(z)dz = 0. |
|
|
|||||
|
|
L2 |
|
|
|
|
й |
|
|
|||
|
|
|
γ1 |
|
|
γ2 |
|
|
|
|
||
|
|
|
|
|
|
|
и |
|
|
|
||
|
|
|
∫ f (z)dz + ∫ f (z)dz + |
∫ f (z)dz = 0. |
|
|
||||||
|
|
|
L |
|
L1 |
|
L2 |
|
|
|
|
|
|
|
|
|
|
|
р |
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
з |
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
п |
|
|
|
|
|
|
|
|
1 |
2 |
|
|
е |
|
|
|
|
|
Рис. 6 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
Зд сь внешний контур обходится против часовой, а внутренние – |
||||||||||||
Р |
|
|
|
|
|
|
|
|
|
|
|
|
по часовой стрелке. Теорема доказана. |
|
|
|
|
|
|||||||
Изменив направление обхода внутренних контуров L и L , |
бу- |
|||||||||||
дем иметь следующее: |
|
|
|
|
|
|
|
|
||||
|
|
|
|
∫ f (z)dz = ∫ f (z)dz + ∫ f (z)dz, |
|
|
||||||
|
|
|
|
L |
|
L1 |
|
|
L2 |
|
|
|
29
