
- •ЛЕКЦИЯ № 1
- •§ 1. Области и их границы
- •§ 3. Элементарные ФКП
- •ЛЕКЦИЯ № 2
- •§ 4. Производная ФКП. Условия Коши – Римана
- •§ 5. Аналитические ФКП
- •ЛЕКЦИЯ № 3
- •§ 7. Интеграл от функции комплексного переменного
- •§ 8. Теорема Коши
- •§ 9. Формула Коши
- •ЛЕКЦИЯ № 4
- •§ 10. Числовые и функциональные ряды ФКП
- •§ 12. Ряд Лорана ФКП
- •ЛЕКЦИЯ № 5
- •§ 13. Особые точки ФКП
- •ЛЕКЦИЯ № 6
- •Практические занятия
- •Ответы
- •ТИПОВОЙ РАСЧЕТ
- •Литература
Известные теоремы для непрерывности функции действительного переменного справедливы и для ФКП.
Если функция непрерывна в каждой точке множества, то она называется непрерывной на этом множестве. Точками разрыва
называют точки, |
в которых нарушаются условия непрерывности |
|||||||||||||
функции. |
|
|
|
|
|
§ 3. ЭЛЕМЕНТАРНЫЕ ФКП |
|
|
У |
|||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
Т |
||||||
|
Под элементарными функциями ФКП аргумента |
|||||||||||||
|
z = x +iy по- |
|||||||||||||
нимаются обычно следующие функции: |
|
Н |
|
|||||||||||
|
f (z) = az +b, |
(a,b Z) – линейная функция; |
|
|||||||||||
|
f (z) = zn (n – целое) – степенная функция; |
|
||||||||||||
|
f (z) = |
|
az +b |
, |
(a,b,c, d Z) |
– дробно-линеБная функция; |
|
|||||||
|
|
|
|
|||||||||||
|
|
|
|
cz + d |
|
|
и |
|
|
|
||||
|
f (z) = |
a0 zn + a1zn−1 + + an |
– общаяйрациональная функция; |
|||||||||||
|
|
|||||||||||||
|
|
|
|
|
|
|
|
р |
|
|
|
|
||
|
|
|
|
b zm +b zm−1 + +b |
|
|
|
|
|
|
||||
|
|
0 |
|
|
1 |
m |
|
|
|
|
|
|
||
|
f (z) = |
|
|
1 |
|
1 |
– функция Жуковского, |
|
|
|
||||
|
|
|
2 z + z |
|
|
|
||||||||
а также показательная, логарифмическаяо |
, тригонометрические, ги- |
|||||||||||||
|
|
|
|
з |
|
|
|
|
|
|
||||
перболические функцтобратные тригонометрические функции. |
||||||||||||||
|
1. Пока ательная функция еz для любого комплексного числа |
|||||||||||||
|
о |
|
|
|
|
|
|
|
|
|||||
z = x +iy |
|
|
пределяетсяиформулой |
|
|
|
|
|
||||||
имеем |
|
|
|
w = ez = ex+iy = ex eiy |
= ex (cos y +i sin y) . |
(3) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Р |
Положивп |
в (3) |
y = 0 , видим, |
что для действительных |
z = x |
|||||||||
ez |
= ex . При |
x = 0 получаем формулу Эйлера: |
|
|
||||||||||
|
|
|
|
|
|
|
eiy = cos y + isin y . |
|
|
|
||||
Для показательной функции справедливы соотношения:
9

|
|
|
|
|
|
|
|
|
z |
|
z |
|
z +z |
|
|
|
|
|
ez1 |
|
|
|
z |
|
−z |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
e 1 |
e |
|
2 = e |
1 |
|
2 |
; |
|
|
|
|
|
|
= e 1 |
|
|
|
2 . |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ez2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Докажем первую из этих формул: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
|||||||||||||||||||
|
|
|
|
|
|
ez1 ez2 = ex1 +iy1 ex2 +iy2 = ex1 ex2 eiy1 eiy2 = |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
= ex1 +x2 (cos y |
+ isin y |
) (cos y |
2 |
|
+ isin y |
2 |
) = |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
[cos y cos y |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
Н |
|
|
||||||||||||
|
x |
+x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
2 |
|
− sin y |
sin y |
|
+ i(cos y |
sin y |
|
|
|
+ sin y |
cos y |
|
|
||||||||||||||||||||||||||
= e 1 |
|
|
2 |
2 |
2 |
|
2 |
)]= |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||||
|
|
= e |
x |
+x |
|
[cos(y1 |
+ y2 ) + isin(y1 |
+ y2 )]= e |
x +x |
|
|
e |
i( y + y ) |
= |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
Б |
2Т |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
= e(x1 +x2 )+i( y1 + y2 ) = ez1 +z2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
что и требовалось доказать. |
|
|
|
|
|
й |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
Аналогично доказывается и вторая формула. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
Функция ez |
является периодическойс ч сто мнимымпериодом2πi : |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
||||
|
|
ez +2πki |
= ex+i( y +2πk) = ex |
(cos(иy + 2πk) + isin(y |
+ 2πk)) |
= |
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
= ex (cosрy + isin y) = ez . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ра- |
|||
|
Из формулы (3) в дно, ч о модуль показательной функции e |
|
||||||||||||||||||||||||||||||||||||||
вен ex , а аргумент – y , т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
z |
|
x |
; |
arge |
z |
= y; |
|
|
Arge |
z |
|
= y + 2πk. |
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
зe = e |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
е |
|
|
|
|
|
|
|
|
|
|
|
функция |
w = Ln z |
|
|
определяется |
|
|
как |
|||||||||||||||||||||
|
2. Логарифмическая |
|
|
|
|
|
||||||||||||||||||||||||||||||||||
функцияп, обратная показательной. Число w называется логариф- |
||||||||||||||||||||||||||||||||||||||||
мом числа z , если ew = z. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Рu |
Положив z = reiϕ , w = u +iv , |
получим eu+iv |
= reiϕ . |
Отсюда |
||||||||||||||||||||||||||||||||||||
e |
= r ; v = ϕ+ 2πk , |
u = ln r , где ln r |
– натуральный логарифм по- |
|||||||||||||||||||||||||||||||||||||
ложительного числа r . Следовательно,
10
|
|
|
w = Ln z = ln r +i(ϕ+ 2πk)= ln |
|
z |
|
+i(arg z + 2πk), |
|
|
(4) |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
где k – любое целое число. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Эта |
формула |
показывает, |
|
|
что логарифмическая |
|
функция |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
У |
комплексного аргумента имеет бесконечно много значений. При |
||||||||||||||||||||||||||||||||||||||
k = 0 |
будем иметь так называемое главное значение логарифма, |
|||||||||||||||||||||||||||||||||||||
которое обозначается символом |
ln z : |
|
|
|
|
|
|
|
|
|
|
Т |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
ln z = ln |
|
z |
|
+i arg z. |
|
|
|
|
Н |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Б |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Если z = x > 0 , то arg z = 0 и |
|
ln z = ln |
|
z |
|
= ln x . |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
Из формулы (4) следует, что |
|
|
|
|
|
|
|
й |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
Ln(z1 z2 ) = Ln z1 + Ln z2 ; |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
Ln |
z1 |
|
|
= |
Ln z |
− Ln z |
|
; |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
рn |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
z2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
Ln zn |
= nиLn z ; |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Ln z |
|
|
|
|
Ln z . |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
= n |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
3. |
Тригонометр |
|
тческ е функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
iz |
− e |
−iz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
iz |
+ e |
−iz |
|
|
|
|
|
|||||
|
|
|
|
|
иe |
|
|
; |
|
|
|
cos z = |
|
|
|
|
; |
|
|
|
|
|||||||||||||||||
|
п |
|
sinz |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
з |
|
|
2i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
(5) |
||||||
ческие |
о tgz = sin z ; |
|
|
|
ctgz = cos z . |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
cos z |
|
|
|
|
|
|
|
|
|
|
|
|
sin z |
|
|
|
|
|
|
|||||||||||||
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Для д йствительных z = x |
эти определения дают тригонометри- |
|||||||||||||||||||||||||||||||||||||
|
функции действительного аргумента: |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
eix −e−ix |
1 |
(cos x +i sin x −cos x +i sin x)= |
2i sin x |
|
|
|||||||||||||||||||||||||||||||
sin z = |
|
2i |
= |
|
|
|
= sin x. |
|||||||||||||||||||||||||||||||
|
2i |
2i |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
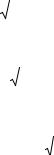
Функции (5) сохраняют многие свойства тригонометрических функций действительного аргумента. Так, например, из периодич-
ности функции ez с периодом 2πi , |
|
функции sin z |
и cos z имеют |
||||||||||||||
период 2π , функции tg z |
и ctg z – период π . Все известные триго- |
||||||||||||||||
нометрические тождества остаются в силе и для тригонометриче- |
|||||||||||||||||
ских функций (5). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Т |
||
|
В отличие от тригонометрических функций действительного ар- |
||||||||||||||||
гумента модули функций sin z и cos z могут быть больше единицы. |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Н |
||
|
4. Обратные тригонометрические функции определяютсяУкак |
||||||||||||||||
функции, обратные по отношению к тригонометрическим. |
|||||||||||||||||
|
Число w называется |
арксинусом |
|
|
|
Б |
|
||||||||||
|
числа |
z |
(обозначение |
||||||||||||||
w = Arcsin z ), если z = sin w : |
|
|
|
й |
|
|
|
||||||||||
|
|
z |
= sin w = |
eiw −e−iw |
|
|
|
|
|
||||||||
|
|
|
|
|
2i |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или |
|
|
|
и |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
e2iw − 2izeiw −1 = 0. |
|
|
|
|
|
||||||||||
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Решая это квадра ное уравнениеротносительно eiw , найдем: |
||||||||||||||||
|
|
и |
оiw |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
− z |
2 |
, |
|
|
|
|
|
|
|
||||
|
|
|
e |
= iz + |
|
|
|
|
|
|
|
|
|||||
откуда |
о |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
з iw = Ln(iz + |
|
1− z2 |
) |
|
|
|
|
|
|||||||
е |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Р |
п w = Arcsin z = −i Ln(iz + |
1− z2 ) . |
|
|
|
||||||||||||
Многозначность этой функции определяется двузначностью корня и бесконечнозначностью логарифма.
Аналогично определяются другие обратные тригонометрические функции:
12
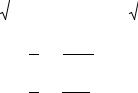
|
|
|
|
|
|
|
|
|
|
|
Arccos z = −i Ln(z + z |
2 |
−1) |
|
− z |
2 |
; |
||||
|
= −i Ln z + i 1 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
Arctg z = − 2i Ln 11+−iziz ; Arcctg z = 2i Ln zz +−ii .
5. Гиперболические функции
|
|
|
|
|
|
ez − e−z |
|
|
|
|
|
ez |
+ e−z |
|
Н |
У |
|||||||
|
|
|
shz = |
|
|
|
2 |
|
; chz = |
|
|
|
2 |
; |
|
Т |
|||||||
|
|
|
|
|
|
|
= sh z |
|
|
cthz = ch z . |
|
|
|
(6) |
|||||||||
|
|
|
|
|
thz |
; |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
ch z |
|
|
|
|
|
sh z |
|
|
|
|
||||
|
Функции sh z и ch z |
|
|
|
|
|
|
|
|
й |
|
|
th z и cth z |
||||||||||
|
периодические с периодомБ2πi ; |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
и |
|
|
|
|
||||||
имеют период πi . Опираясь на формулы (5) и (6), легко получить |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
р |
|
|
|
|
|
|
|
|
|
||||
следующие формулы, выражающ е г перболические функции че- |
|||||||||||||||||||||||
рез тригонометрические: |
о |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
sh z |
= −i sin iz ; |
|
|
|
|
|
|
|||||||
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
ch z = cosiz ; |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
th z = −i tg iz ; |
|
|
|
|
|
|
|
|||||||
|
|
о |
|
|
|
|
|
cth z = i ctg iz . |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
6. Общая степеннаяифункция |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
п |
з |
= z |
z2 |
= e |
|
Ln zz2 |
|
|
|
z |
2 |
Ln z |
|
|
|
|
||||||
|
|
|
|
w |
|
|
|
|
|
1 |
= e |
|
1 . |
|
|
|
|||||||
е |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Р |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13
