Кафедра «Высшая математика № 1»

У

Т

Н

КУРС ЛЕКЦИЙ И

й

ПРАКТИКУМ ПО ТЕОРИИБ

ФУНКЦИЙ

КОМПЛЕКСНОГОи

о

ПЕРЕМЕННОГОр

т

и

з

Учебное электронное издание

о

п

е

Р

Авторы :

У

Н. А. Микулик, Т. С. Яцкевич, И. Н. Катковская, Е. А. Герасимова,

Л. А. Раевская, Т. И. Чепелева

Т

Рецензенты

Н

А. Н. Исаченко, М. Н. Покатилова

Э 45 Курс лекций и практикум по теории

Б

комплексного пере-

менного/ Н.А. Микулик [и др.]. – Минск: БНТУ, 2011. – 89 с.

теорет

ческ

материал по избранным гла-

В данном курсе лекций излагается

вам теории функций комплексного пе еменногофункций(ТФКП), который предусмотрен

программой по математике для студентов маш ностроительных специальностей

приведено

втузов. В каждой из 6 лекций

дистаточное количество задач и примеров

с подробными решениями

ациями.

иллюст

Также подобраны ма ериалы для 4 практических занятий по наиболее важным

темам. Все примеры снабжены

ве ами. В работе имеется еще и типовой расчет

по теории функций комплексного переменного.

Данное пособ е предназначено для студентов машиностроительных специаль-

з

ностей, а также оно будет полезно для преподавателей, читающих лекции и прово-

дящих занятия ТФКП. Избранная авторами методика изложения делает пособие

по

вполне приг дным дляисамостоятельного овладения предметом.

п

Бел русский национальный технический университет

е

р-т Независим сти, 65, г. Минск, Республика Беларусь

Т л.(017)292-77-52 факс (017)292-91-37

Р

E-mail: tchepeleva@gmail.com

http://www.bntu.by/fitr-vm1.html

егистрационный № ЭИ БНТУ/ФИТР48-5.2011

© Микулик Н.А., Яцкевич Т.С., 2011

СОДЕРЖАНИЕ

ЛЕКЦИЯ № 1............................................................................................

4

§ 1. Области и их границы

..................................................................

4

§ 2. Определение функции комплексного переменного (ФКП).

Предел, непрерывность.......................................................................

5

§ 3. Элементарные ФКП.....................................................................

9

ЛЕКЦИЯ № 2 ............................................................................................

14

§ 4. Производная ФКП. Условия ............................Коши – Римана

14

§ 5. Аналитические ФКП....................................................................

У19

Н

§ 6. Геометрический смысл .....аргумента и модуля производной

21

ЛЕКЦИЯ № 3............................................................................................

Т

24

Б

§ 7. Интеграл от функции комплексного ...................переменного

24

§ 8. Теорема Коши...............................................................................

27

§ 9. Формула Коши..............................................................................

30

ЛЕКЦИЯ № 4............................................................................................

36

и

§ 10. Числовые и функциональные .................................ряды ФКП

36

§ 11. Ряд Тейлора функции ................комплексного переменного

38

р

§ 12. Ряд Лорана ФКП.........................................................................

й

41

ЛЕКЦИЯ № 5............................................................................................

47

§ 13. Особые точки ФКП....................................................................

47

т

§ 14. Нули аналитических функций. Связь между нулями и

полюсами..............................................................................................

51

функции

§ 15. Поведение функцииов окрестности бесконечно удаленной

точки.....................................................................................................

55

з

ЛЕКЦИЯ № 6............................................................................................

57

о

§ 16. Вычет

в конечной изолированной особой точке.

Осн вная те рема о вычетах..............................................................

57

п

Практические занятия..............................................................................

66

Занятие № 1..........................................................................................

66

Занятие № 2..........................................................................................

66

Р

Занятие № 3..........................................................................................

67

еЗанятие № 4..........................................................................................

68

ТИПОВОЙ РАСЧЕТ

................................................................................

70

Литература ................................................................................................

89

Пусть имеем множество Е точек z = x +iy

комплексной плос-

кости Z.

У

Точка z0 называется внутренней точкой множества Е, если все

Т

точки достаточно малого круга с центром в точке z0 принадлежат Е.

Н

Точка z1 , принадлежащая или не принадлежащая множеству Е,

называется граничной точкой множества Е, если любой круг с цен-

Б

тром

z1 содержит точки, как принадлежащие, так и не принадлежащие

Е.

Множество всех граничных точек множества Е называется гра-

ницей множества Е.

Точка z называется внешней точкой множества Е, если вместе

с этой точкой множеству Е не пр надлеж т и некоторый круг с

центром в z.

р

й

П имеиы

т

1.

Множество

z

<1

с держит только внутренние точки. Окруж-

ность

z

=1

– гран ца э

огомножества.

з

состоит только из внутренних точек.

2. Множество

z

>1

Множество

3.

и

1≤

z −i

≤ 2 содержит внутренние и граничные точки.

п

Областью называется множество D точек плоскости Z, облада-

ющее следующими свойствами:

е

•

D состоит из одних внутренних точек (свойство открытости);

Р

•

любые две точки,

принадлежащие D, можно соединить непре-

Б

t1 ≤ t ≤ t2 , является параметрическим уравнением непрерывной

кривой L на комплексной плоскости.

й

Если ϕ(t) , ψ(t) непрерывны и имеют непрерывные производ-

ные, причем [ϕ'(t)]2 +[ψ'(t)]2 ≠ 0 ,

ли

, то кривая L называется

t1 ≤ t ≤ t2

гладкой. Замкнутая кривая, не

меющая точек самопересечения,

называется замкнутым конту ом

просто контуром.

о

В дальнейшем будем считать, что г аницы рассматриваемых обла-

стей состоят из конечного числа замкнутых контуров, разрезов и точек.

т

рс ст ит вся граница области D, назы-

Число частей, из ко рых

вается порядком связн с и э

й

бласти (рис. 1).

и

з

о

п

е

Рис. 1

в) четырехсвязная область

Р

Говорят, что на множестве Е задана функция

w = f (z) ,

(1)

если каждой точке z E поставлены в соответствие одна или не-

сколько точек w. В первом случае функция называется однознач-

ной, а во втором – многозначной.

У

Множество Е называется множеством определения функции

f (z) , а множество K всех значений

Т

w, которые f (z) принимает на

Е – множеством изменения функции f (z) .

Н

Если Е и K – области, то говорят об области задания и области зна-

чений функции w = f (z) . Если z = x +iy

и w = u +iv , то

w = f (z) =

= f (x +iy) = u(x, y) +iv(x, y) , а

Б

u(x, y) = Re f (z),

й

(2)

v(x, y) = Im f (z) .

едставить

Таким образом, задание функции (1) комплексного переменного

равносильно заданию двух функц й (2) двух де ствительных пере-

менных.

р

о

в виде (рис. 2):

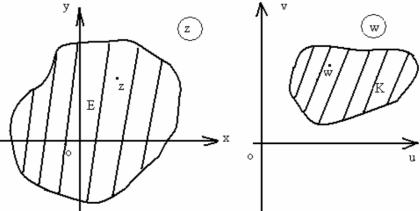
Геометрически это можно п

т

и

з

о

п

е

Р

Рис. 2

и точками множества К на плоскости uOv функция ω = f (z)

уста-

навливает соответствие. Или функция

w = f (z)

отображает точки

множества Е в точки множества К.

У

В этом случае точки множества К

называются образами соот-

ветствующих точек множества Е.

Т

Если каждая точка

z E при помощи функции w = f (z)

отоб-

ражается в единственную точку w K и,

наоборот, каждая точка

Н

w K отображается обратной функцией z = ϕ(ω) в единственную

точку множества Е, то говорят, что между множествами Е и К уста-

новлено взаимно-однозначное соответствие.

Б

В таком случае функции w = f (z) и z = ϕ(w)

называются одно-

значными, а отображение однолистным.

2

й

и

Пример

Пусть w = z

р

x = Rcost;

y = Rsint

. Найти изоб ажен е л н

(0 ≤ t ≤ π) в плоскости w.

т

Решение.

z

= x + iy = Rcost + iRsin t = Reit . w = R2e2it .

w

= R2 ;

arg w = 2t. При

и

0 ≤ t ≤ π

0о≤ arg w ≤ 2π (рис. 3).

y

з

v

W

п

Z

е

0

0

Р

оR

R2

x

u

Пусть функция w = f (z) – однозначная,

определена для любых

z E , исключая, быть может, точку z0 .

f (z)

Число

А≠ ∞ называется пределом функции

в точке

z0

У

lim f

(z)= A , если для ε > 0

δ(ε)> 0 такое,

что для всех

z ,

z→z0

удовлетворяющих

неравенству

0 <

z − z0

< δ,

выполняется

нера-

венство

f (z)− A

< ε.

f (z) при

A = ∞ называется пределом функции

z → z0

lim f (z) =∞ ,

Т0

Б

z→z

если для R > 0 δ > 0 такое,

что из неравества

0 <

z − z0

< δ

сле-

дует неравенство

f (z)

> R.

Н

Пусть A = B +iC и f (z)= u(x, y)+iv(x, y),

причем z0 = x0 +iy0 .

Теорема. Если существует

lim

f

(z)= A = B + iC,

то существует

р

й

u(x, y)= B

z =z0

lim

и

lim

v(x, y)= C.

x→x

о

x→иx

y→y0

т

y→y0

0

0

Доказательство

еоремы пред ставляем читателю.

и

Из теоремы следует, ч все теоремы о конечных пределах для

функций действ тельного переменного справедливы для ФКП.

з

Пусть теперь f

(z) определена в точке z0

и ее окрестности.

Функция f (z)

на ывается непрерывной в конечной точке

z0 ,

если lim

f (z)

= f (z0 ).

0

п

z→z0

(

)

(

Если

z − z

= ∆z,

тогда lim

f

z

+∆z

− f

z

= lim ∆w = 0.

о0

∆z→0

0

0 )

∆z→0

На основании теоремы имеем,

что если

lim f (z)= B + iC = f (z

),

ето lim

z→z0

u(x, y)= B = u(x0 , y0 )

и

lim

v(x, y)= C = v(x0 , y0 ) .

x→x0

x→x0

y→y0

y→y0

РСледовательно,

если w = f (z)

непрерывна

в

конечной точке