
Математика№3
.pdf
Министерство образования Республики Беларусь Белорусский национальный технический университет
Кафедра высшей математики № 1
|
|
ɍ |
|
|
Ɍ |
|
|
ɇ |
|
Ȼ |
|
|
МАТЕМАТИКА |
|
|
Контрольная работа № 3 для студентов инженерно-технических |
|
|
специальностей заочной формы обучения. |
|
|
ɢ |
|
|
Методические указания и индивидуальныеɣ |
задания |
|
ɪ |
|
|
Учебное электронное издание |
|
|
ɨ |
|
|
ɬ |
|
|
ɢ |
|
|
ɡ |
|
|
ɨ |
|
|
ɩ |
|
ɟ |
|
|
Ɋ |
Минск БНТУ |
|
2 0 1 1 |
|
|

УДК 512.64 (075.8) ББК 22.1я7
М 93
С о с т а в и т е л и : |
|
|
|
А.Н. Андриянчик, В.А. Казакевич, Н.А. Микулик, |
ɍ |
||
Л.А. Раевская, В.И. Юринок, Т.С. Яцкевич |
|||
|
|||
Р е ц е н з е н т ы : |
Ɍ |
||
|
|
||
А.Н. Исаченко, М.Н. Покатилова |
ɇ |
|
|
|
|
||
Настоящие методические указания и контрольные задания |
|||
предназначены для студентов-заочников второго курса инженернотехническихспециальностей БНТУ.
Издание содержит программу по высшей математике, пере- |
|
|
ɣ |
чень рекомендуемой литературы, основныеȻпонятия по теории |
|
курса высшей математики, типовые примеры и контрольные за- |
|
дания. |
ɢ |
|
|
Студент должен изучить теоретический материал по учебни- |
|
|
ɪ |
ку, разобрать приведенные образцы решения типовых примеров и |
|
задач, а затем выполнить контрольные задания, соответствующие |
|
номеру его варианта. Номер варианта определяется двумя по- |
|
следними цифрами шифра зачетной книжки, если это число не |
|
ɬ |
|
больше 30. Если номерɨшифра больше 30, следует от него отнять |
|
число, кратное 30. В каждом из семи заданий нужно выполнить |
|
ɢ |
|
номер, соответствующий номеру варианта. |
|
ɡ |
|
Например, если шифр содержит две последние цифры 62, |
|
номерами этого варианта будут 1.2; 2.2; 3.2; 4.2; 5.2; 6.2; 7.2. |
|
ɨ |
|
Белорусский национальный технический университет |
|
ɩ |
|
пр.Независимости, 65, г. Минск, Беларусь |
|
тел. (017) 292-77-52 факс (017) 292-91-37 |
|
Ɋ |
|
ɟРегистрационный № БНТУ/ФИТР48-4.2011 |
|
© БНТУ, 2011
Балашова Е.Б. – компьютерный набор, графика, верстка
2
|
ОГЛАВЛЕНИЕ |
|
|
|
|
ПРОГРАММА................................................................................. |
|
|
4 |
1. РЯДЫ............................................................................................... |
|
|
5 |
|
|
1.1. Числовые ряды. Основные определения. |
|
|
|
|
Признаки сравнения................................................................ |
|
|
5 |
|
1.2. Достаточные признаки сходимости рядов |
|
|
|
|
с положительными членами................................................... |
|
|
8 |
|
1.3. Знакопеременные ряды. Абсолютная и условная |
|
|
|
|
сходимость. Знакочередующиеся ряды. |
|
|
ɍ |
|
|
|
Ɍ |
|
|
Признак Лейбница................................................................. |
|
|
10 |
|
1.4. Функциональные ряды. Область сходимости |
|
|
|
|
функционального ряда. Степенные ряды............................ |
|
|
12 |
|
1.5. Разложение функции в ряд Тейлора .................................... |
|
|
16 |
|
1.6. Применение степенных рядов |
ɇ |
|
|
|
в приближенных вычислениях............................................. |
|
|
18 |
|
ɣ |
|
|
|
|
1.7. Ряд Фурье функции, заданной на отрезкеȻдлиной 2 ........... |
|
22 |
|
|
1.8. Ряд Фурье функции, заданной на отрезке длиной 2l |
.......... |
27 |
|
2. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ |
|
|
|
|
|
ɢ |
|
|
|
|
ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕНЫХ.............................. |
|
|
28 |
|
ɪ |
|
|
|
|
2.1. Определенный интеграл по фигуре. |
|
|
|
|
Основные понятия и свойства.............................................. |
|
|
28 |
|
ɨ |
|
|
|
|
2.2. Вычисление двойных и тройных интегралов |
|
|
|
|
в декартовых координатах.................................................... |
|
|
30 |
|
ɬ |
|
|
|
|
2.3. Замена переменных в кратном интеграле............................ |
|
|
36 |
|
2.4. Криволинейные интегралы I и II рода................................. |
|
|
42 |
|
ɢ |
|
|
|
|
2.5. Поверхностные интегралы I и II рода.................................. |
|
|
43 |
|
2.6. Вычисление криволинейных интегралов I и II рода........... |
|
45 |
|
|
2.7. Вычисление поверхностных интегралов I и II рода. |
|
|
|
|
ɨ |
|
|
|
|
Связьɡмежду ними................................................................. |
|
|
47 |
|
2.8. Формулы Грина, Стокса, Остроградского-Гаусса.............. |
|
49 |
|
ɩ |
|
|
|
|
3. ЭЛЕМЕНТЫ ОПЕРАЦИОННОГО ИСЧИСЛЕНИЯ................. |
|
53 |
||
|
3.1. Оригинал и его изображения................................................ |
|
|
53 |
|
3.2. Основные теоремы операционного исчисления................. |
|
55 |
|
|
3.3. Отыскание оригинала по изображению............................... |
|
|
56 |
Ɋ |
|
|
|
|
ɟ |
3.4. Решение дифференциальных уравнений |
|
|
|
|
и систем дифференциальных уравнений |
|
|
|
|
операционным методом........................................................ |
|
|
59 |
|
КОНТРОЛЬНАЯ РАБОТА №3 ................................................... |
|
|
61 |
|
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА......................................... |
|
|
72 |
3
|
|
|
ПРОГРАММА |
|
|
|
|
|
Ряды |
|
|
|
Числовые ряды. Сходимость и сумма ряда. Действия над ря- |
||||
|
дами. Необходимое условие сходимости. |
|
|
||
|
Достаточные признаки сходимости рядов с положительными |
||||
|
членами. |
|
|
|
ɍ |
|
|
|
|
|
|
|
Знакопеременные ряды. Абсолютная и условная сходимость. |
||||
|
Знакочередующиеся ряды. Теорема Лейбница. |
|
Ɍ |
||
|
|
|
|||
|
Функциональные ряды. Область сходимости. Равномерная |
||||
|
сходимость. Признак Вейерштрасса. |
ɇ |
|||
|
Степенные ряды. Теорема Абеля. Интервал и радиус сходи- |
||||
|
мости степенного ряда. |
|
|
|
|
|
Ряды Тейлора и Маклорена. Разложение функций в степен- |
||||
|
ные ряды. |
|
|
|
|
|
Применение рядов к приближенным вычислениям. |
|
|||
|
|
|
ɣ |
|
|
|
Ряды Фурье по тригонометрическим системамȻ. Разложение |
||||
|
функций в ряды Фурье. Условия поточечной сходимости и схо- |
||||
|
|
|
ɢ |
|
|
|
димости в среднем. Применение рядов Фурье. |
|
|
||
|
|
Интегральное исчисление функций |
|
||
|
|
нескольких переменных |
|
|
|
|
Определенный интегралɪпо фигуре, его механический смысл. |
||||
|
Свойства интегралов по фигуре. |
|
|
||
|
|
ɬ |
|
|
|
|
Вычислениекратныхɨинтеграловповторныминтегрированием. |
||||
|
Замена переменных в кратных интегралах. |
|
|
||
|
Вычисление криволинейных и поверхностных интегралов I и |
||||
|
ɡ |
|
|
|
|
|
II рода, их приложенияɢ |
. Формулы Грина, Стокса, Остроградско- |
|||
|
го-Гаусса. |
|
|
|
|
|
ɨ |
Элементы операционного исчисления |
|
||
|
ɩ |
|
|
|
|
|
Преобразование Лапласа. Теорема существования и единст- |
||||
ɟ |
|
|
|
|
|
|
венности. Класс оригиналов и класс изображений. |
|
|
||
Ɋ |
Основные теоремы операционного исчисления. |
|
|||
Определение оригинала по изображению с помощью таблиц |
|||||
и второй теоремы разложения. |
|
|
|||
Решение линейных дифференциальных уравнений и систем |
|||||
операционным методом. |
|
|
|||
4

1. РЯДЫ
1.1. Числовые ряды. Основные определения. Признаки сравнения
Выражение
u1 u2 ... n ... |
n , |
(1.1) |
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɍ |
|
|
где ( un ) – последовательность чисел, называется числовым ря- |
||||||||||||||||||||
|
дом, |
числа |
u , u |
2 |
,..., u |
n |
, |
– |
членами ряда, |
|
u |
n |
– общим членом |
||||||||
|
ряда. |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
ɍ |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Суммы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S1 |
u1, S2 |
|
u1 u2 , |
..., |
Sn |
1 |
u2 ... |
|
un , ... |
|
(1.2) |
||||||||
|
называются частичными суммами ряда (1.1). |
|
|
|
ɇ |
|
|||||||||||||||
|
|
Если существует конечный предел |
|
Ȼ |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
lim S n |
S , |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
то ряд (1.1) называется сходящимся, а число S – его суммой. Если |
||||||||||||||||||||
|
же lim S n |
не существует или lim S n =ɣ, то ряд называется расхо- |
|||||||||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
дящимся. |
|
|
|
|
|
|
|
|
ɪ |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
ɢ |
|
|
|
|
|
|
||||
|
|
Если в ряде отбросить первые k членов, то получится ряд |
|||||||||||||||||||
|
|
|
|
|
|
|
|
ɨ |
|
uk 1 |
uk |
2 ... , |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
rk= |
|
n |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
n k |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
называемый k-м остатком ряда (1.1). |
|
|
|
|
|
|
|
|||||||||||||
|
|
Необходимыйɬпризнак сходимости. Если ряд (1.1) сходит- |
|||||||||||||||||||
|
ся, то |
|
ɢlim un |
0 . |
|
|
|
|
|
|
|
|
(1.3) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
ɨ |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
0 , то ряд (1.1) расходится. |
|
||||||||||
|
|
Следствиеɡ. Если lim un |
|
|
|||||||||||||||||
|
ɩ |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1 |
|
|
|
|
|
|
гармоническим |
|
рядом. |
|
|
||||||||
|
|
Ряд |
|
|
|
называется |
|
Для него |
|||||||||||||
|
|
n |
1 |
n |
|
|
|
||||||||||||||
|
lim un 0 , но ряд расходится. |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɟ |
Признаки сравнения. Рассмотрим числовые ряды с неотри- |
||||||||||||||||||||
Ɋ |
цательными членами |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
n |
; |
|
|
|
|
|
|
|
|
(1.4) |
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
. |
|
|
|
|
|
|
|
|
(1.5) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
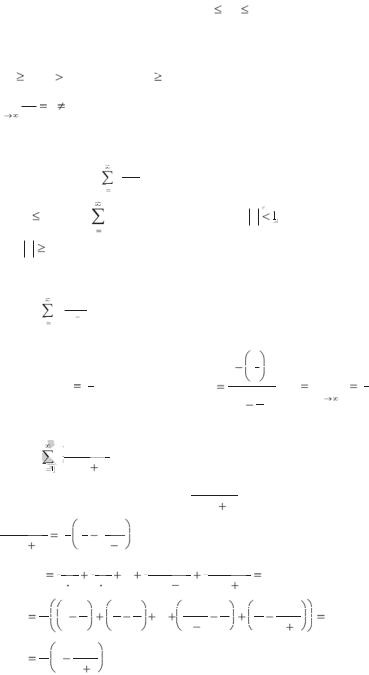
|
|
Теорема 1. Признак сравнения. Если, начиная с некоторого |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
номера, |
выполняются неравенства |
0 |
un |
vn , то из сходимости |
|||||||||||||||||||
|
ряда (1.5) следует сходимость ряда (1.4), а из расходимости ряда |
|||||||||||||||||||||||
|
(1.4) следует расходимость ряда (1.5). |
|
|
|
|
|
|
|
||||||||||||||||
|
|
Теорема 2. Предельный |
|
признак |
|
сравнения. |
|
Если |
||||||||||||||||
|
un |
|
, vn |
|
|
для |
всех |
n |
0 |
и |
существует |
конечный предел |
||||||||||||
|
lim un |
|
l |
|
0 , то ряды (1.4) и (1.5) сходятся или расходятся од- |
|||||||||||||||||||
|
n |
vn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
новременно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Замечание. При использовании признаков сравнения часто |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
ɍ |
|
применяется ряд |
|
|
|
, сходящийся при p > 1 и расходящийся |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
n |
1 |
n p |
|
|
|
|
|
|
|
|
|
Ɍ |
||
|
при p |
1 и ряд |
|
|
|
aq n-1 , сходящийся при |
q |
и расходящийся |
||||||||||||||||
|
|
|
|
|
|
|
|
n |
|
1 |
|
|
|
|
|
|
|
|
|
|
ɇ |
|
|
|
|
при |
q |
1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ȼ |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Примеры. Исследовать на сходимость ряды и в случае схо- |
||||||||||||||||||||||
|
димости найти сумму ряда. |
|
|
|
ɣ |
|
|
|
|
|
||||||||||||||
|
|
1. |
|
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
n |
1 |
|
3 n |
1 |
|
|
|
|
|
|
|
ɢ |
|
|
|
|
|
|
|||
|
|
Решение. Данный ряд – геометрическая прогрессия со зна- |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
ɪ |
|
1 |
1 |
n |
|
|
|
||||
|
менателем q |
1 . Следовательно, |
S |
n |
|
3 |
, S |
lim S |
n |
3 , |
||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
ɨ |
|
|
|
|
|
1 |
|
n |
2 |
||||
|
|
|
|
|
|
|
ɬ |
|
|
|
|
1 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
||||||
|
ряд сходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
ɢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2. |
|
|
|
1 |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
ɡ |
|
|
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
n 1 |
|
4n(n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
ɨРешение. Так |
как |
дробь |
|
|
1 |
1) |
представима в |
|
виде |
||||||||||||||
|
4n(n |
|
||||||||||||||||||||||
|
ɩ |
|
|
|
1 |
1 |
|
|
|
1 |
, то частичная сумма ряда имеет вид: |
|
||||||||||||
|
|
1 |
|
|
|
|
|
n |
|
|||||||||||||||
|
4n(n ) |
|
|
4 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ɟ |
|
|
|
|
1 |
|
|
1 |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
||
Ɋ |
|
S n |
|
|
|
|
|
. . . |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
4 2 8 3 |
4n(n 1) 4n(n 1) |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
1 |
|
1 |
1 |
|
|
|
1 |
1 |
. . . |
|
1 |
|
|
1 |
|
1 |
1 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
4 |
|
2 |
|
|
|
2 |
3 |
|
n |
1 |
n |
|
n |
n 1 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
1 |
|
1 |
|
1 |
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|

|
|
Следовательно, |
lim S n |
|
1 |
|
lim |
1 |
|
|
|
|
1 |
|
|
|
1 |
, ряд сходится и |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
n |
1 |
4 |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
4 n |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
его сумма равна 1/4. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
3. 2 + 5 + 8 + 11 + .... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
Решение. Данный ряд – сумма членов арифметической про- |
|||||||||||||||||||||||||||||||||||||||||||||||
|
грессии с разностью d = 3, поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɍ |
|||||||||||||||||||||||||||||||
|
|
S n |
|
|
|
2a1 |
|
d (n 1) |
|
n |
|
4 3(n 1) |
n |
|
(1 3n)n |
, |
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
n)n |
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
lim |
|
Sn |
(1 |
|
|
|
|
|
|
ряд расходится. |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Проверить, выполняется ли необходимый признак сходимо- |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɍ |
|||
|
сти ряда. В случае выполнения установить, сходится ли ряд с по- |
||||||||||||||||||||||||||||||||||||||||||||||||
|
мощью признака сравнения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɇ |
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
4. |
2 |
|
|
|
|
... . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ȼ |
|
|
|
|
||||||||||||||
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
n |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
Решение. lim un |
|
|
|
|
lim |
|
|
1 |
|
|
0 , |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
т.е. |
необходимый |
при- |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
знак не выполняется, ряд расходится.ɣ |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
5. |
|
1 |
|
|
|
|
|
1 |
... |
|
|
|
|
|
1 |
|
|
|
ɢ... . |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
ln 2 |
ln 3 |
|
|
|
|
|
|
|
ln(n |
) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
Решение. lim un |
|
|
|
|
lim |
ɪ1 |
0 , |
т.е. |
необходимый |
при- |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
ln(n |
|
|
1) |
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
знак выполняется. Исследуем сходимость данного ряда с помо- |
||||||||||||||||||||||||||||||||||||||||||||||||
|
щью признака сравненияɬ(теорема 1). Рассмотрим расходящийся |
||||||||||||||||||||||||||||||||||||||||||||||||
|
ряд |
|
1 |
|
. |
Так как |
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
(ln n ) , |
то исходный |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
n 1 |
|
n |
|
|
|
ɢ |
|
|
|
|
|
ln(n ) |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
ряд расходитсяɡ. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
6. |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
ɨ |
|
(2n 1)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
ɩ |
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ɟ |
Решение. |
|
|
lim un |
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
Рассмотрим |
сходя- |
||||||||||||||||||||||||||
|
|
|
|
(2n |
|
|
1)22n 1 |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Ɋ |
щийся ряд |
|
|
|
|
|
|
|
– сумму членов геометрической прогрессии |
||||||||||||||||||||||||||||||||||||||||
n 1 |
|
22n |
1 |
|
|||||||||||||||||||||||||||||||||||||||||||||
со знаменателем |
q |
|
|
1 |
1 . |
Так как |
|
|
|
|
1 |
|
|
|
|
1 |
|
, |
то по |
||||||||||||||||||||||||||||||
|
|
4 |
|
(2n 1)22n 1 |
|
22n 1 |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
теореме 1 исходный ряд сходится.
7

|
|
|
|
|
7. |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
1 |
|
n4 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
Решение. lim un |
|
|
lim |
|
|
n |
|
|
|
0 . |
|
Рассмотрим |
сходящийся |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
n4 |
1 |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|||||||
|
ряд |
|
|
|
|
|
1 |
|
( p |
|
|
|
|
1) и применим предельный признак сравнения |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
n 1 |
|
|
n3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɍ |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
(теорема 2): lim |
|
un |
|
|
|
|
|
|
|
|
|
n |
|
|
|
1 |
|
|
|
n4 |
|
Ɍ |
||||||||||||||||||||
|
|
vn |
|
|
|
|
lim |
|
n4 |
: |
n3 |
|
lim |
4 |
|
0 . Сле- |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
|
n n |
|
|
||||||||||||
|
довательно, данный ряд сходится. |
|
|
|
|
|
ɇ |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
1.2. Достаточные признаки сходимости рядов |
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с положительными членами |
|
|
|
||||||||||||||||||||
|
|
|
|
|
Для знакоположительных числовых рядов имеют место сле- |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɣ |
|
|
|
||||
|
дующие достаточные признаки, по которым можноȻустановить их |
||||||||||||||||||||||||||||||||||||||||||
|
сходимость или расходимость. |
ɢ |
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
1. Признак Даламбера. Если для ряда |
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
(un |
0, |
|
n 1,2,3, ... ) |
|
|
|
|
(1.6) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
un 1 |
|
|
|
|
|
|
|
ɪ |
|
|
|
|
|
|
|
|
|||||||||
|
существует |
|
lim |
|
|
|
|
|
|
|
ɨ |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
un |
|
|
|
|
l |
, то при l < 1 ряд (1.6) сходится, при l > 1 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɬ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
– расходится. При l = 1 вопрос о сходимости ряда остается нере- |
||||||||||||||||||||||||||||||||||||||||||
|
шенным. |
|
|
|
ɢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
Пример 1. Исследовать на сходимость ряды с помощью при- |
||||||||||||||||||||||||||||||||||||||
|
знака Даламбера: |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
1 |
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
a) |
|
|
|
|
|
|
|
|
ɡ |
... |
|
|
|
|
|
|
|
... ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
3 |
|
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 |
|
|
1 2 |
|
1 2 3 |
|
|
|
|
|
|
|
n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
б) |
|
|
|
ɨ |
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
... . |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
10 |
|
|
|
|
|
|
103 |
|
|
10n |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
10 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
ɩРешение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
a) |
un |
|
|
|
|
n |
|
; un 1 |
|
|
|
n |
|
|
|
1 |
. Так как |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
3n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
ɟ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Ɋ |
lim |
un |
1 |
|
|
|
|
lim |
|
(n |
|
|
1)3n |
|
|
lim |
|
n |
1 1 |
|
1 , то ряд сходится. |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
un |
|
|
|
|
|
|
3 |
n |
1 |
|
n |
|
|
|
3n 3 |
|||||||||||||||||||||||||||
n |
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
б) un |
|
|
|
|
n! |
; u n 1 |
|
|
(n 1) ! |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
10n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10n |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
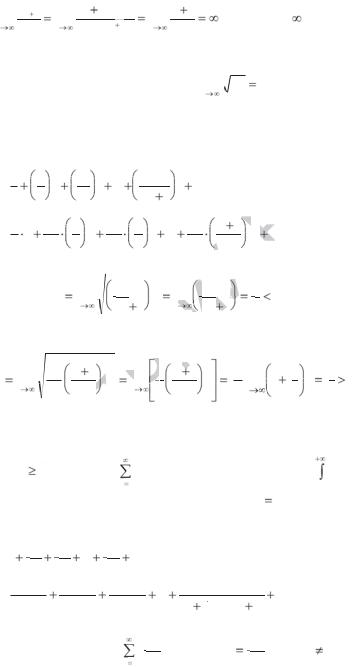
|
lim |
un 1 |
|
lim |
(n |
1) !10n |
|
lim |
n |
1 |
. Так как l = |
, то данный |
||||||||||||||
|
un |
|
|
n!10 |
n |
1 |
|
10 |
|
|||||||||||||||||
|
n |
|
|
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
ряд расходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
2. Радикальный признак Коши. Если для знакоположитель- |
|||||||||||||||||||||||
|
ного ряда (1.6) существует предел |
lim n |
un |
|
|
, то при q < 1 ряд |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
сходится, при q > 1 – расходится. При q = 1 вопрос о сходимости |
|||||||||||||||||||||||||
|
ряда остается нерешенным. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
Пример 2. Исследовать сходимость рядов с помощью ради- |
|||||||||||||||||||||||
|
кального признака Коши: |
|
|
|
|
|
|
|
|
|
|
|
|
|
ɍ |
|||||||||||
|
a) |
1 |
|
2 2 |
|
3 3 . . . |
|
n |
1 |
n |
. . . ; |
|
|
|
|
|
|
|
Ɍ |
|||||||
|
|
5 |
|
9 |
|
|
|
13 |
|
|
|
4n |
|
|
|
|
|
|
|
|
ɇ |
|
||||
|
б) |
1 |
2 |
|
1 |
|
|
3 4 |
|
1 4 |
9 |
. . . |
1 n |
|
|
n2 |
. . . . |
|
||||||||
|
2 |
|
22 |
|
2 |
23 |
3 |
|
|
n |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
2n |
|
Ȼ |
|
|
|
||||||||||||||
|
|
|
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
n |
|
n |
|
|
|
n |
|
|
1 |
|
|
|
|
|
|
|
а) Так как q |
|
lim n |
|
|
|
|
lim |
|
|
1 , то ряд схо- |
|
||||||||||||||
|
|
|
|
|
|
|
ɣ |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
4n |
1 |
|
|
|
4n 1 |
|
|
4 |
|
|
|
|
|
|
|||
|
дится. |
|
|
|
|
|
|
|
|
|
|
|
ɢ |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
ɪ |
|
|
|
|
|
|
|
|
|
|
||||||
|
б) в этом случае |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
|
|
1 n |
e |
|
||||||
|
q |
lim |
n |
1 n 1 n |
|
lim |
1 n 1 |
n |
lim 1 |
|
. |
|||||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
n |
|
2 |
|
n |
|
|
ɨ |
|
n |
|
|
2 n |
|
|
n |
|
2 |
|
||||||
|
|
|
|
|
|
|
n |
|
2 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
ɬ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Следовательно, ряд расходится. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
3. Интегральный признак Коши. Пусть f(x) – непрерывная, |
|||||||||||||||||||||||
|
|
|
|
|
|
|
ɢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
положительная и монотонно убывающая функция, определенная |
|||||||||||||||||||||||||
|
при x |
ɡ |
|
|
|
|
и несобственный интеграл |
f (x) dx |
||||||||||||||||||
|
1. Тогда ряд |
|
n |
|||||||||||||||||||||||
|
|
ɨ |
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
un . |
|
|
|
|||||||
|
сходятся или расходятся одновременно, где f(n) |
|
|
|
||||||||||||||||||||||
|
|
|
Пример 3. Исследовать сходимость рядов с помощью инте- |
|||||||||||||||||||||||
|
ɩ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
грального признака Коши: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
ɟ |
|
1 |
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
2 p |
|
3 p |
|
. . . n p |
. . . ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Ɋ |
a) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
б) |
|
1 |
|
|
|
|
1 |
|
|
1 |
|
|
. |
|
|
1 |
|
|
1) |
|
. . |
|
|
|
||
|
|
2 ln 2 2 3 ln 2 3 4 ln 2 4 |
|
|
(n 1) ln 2 (n |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
Решение. |
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|||||
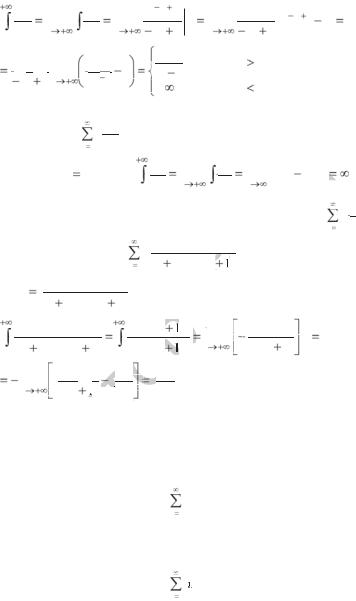
|
a) Исследуемый ряд – |
|
|
. Здесь f (n) |
|
. Если p |
1, то |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
n 1 |
n p |
|
|
|
|
|
|
n p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
lim |
b |
dx |
|
lim |
x |
p |
1 |
b |
|
lim |
|
1 |
(b |
p 1 |
1) |
|
|||||||||
|
1 x p |
|
|
x p |
|
|
|
p 1 1 |
|
|
p 1 |
|
|
||||||||||||||||
|
|
b |
|
|
1 |
b |
|
|
|
|
b |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
p |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
lim |
|
|
1 |
|
|
1 |
|
|
p |
1 , |
если |
|
1, |
|
|
|
|
|
||||||
|
|
p |
|
1 b |
|
|
|
b p |
1 |
|
|
|
|
|
, |
|
если |
p |
|
1, |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
т.е. интеграл сходится при p > 1 и расходится при p < 1. Соответ- |
||||||||||||||||||||||||||||
|
ственно и ряд |
|
|
|
1 |
|
сходится, если p > 1 и расходится, если |
ɍ |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
n |
1 |
n p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
p < 1. При p |
1 имеем |
|
dx |
|
lim |
b |
dx |
|
lim (ln b |
ln 1) |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
, |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
x |
|
b |
|
1 |
x |
|
b |
|
|
|
|
Ɍ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
т.е. интеграл расходится. Следовательно, расходится ряд |
|
|
1 . |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
ɇn 1 |
n |
||
|
б) Исследуемый ряд – |
|
|
|
|
|
|
|
|
. Здесь |
|
|
|
|
|
||||||||||||||
|
|
(n ) ln 2 (n ) |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
Ȼ |
|
|
|
||||||||||
|
f (n) |
|
|
|
|
|
1 |
|
|
|
. Рассмотрим |
ɣ |
|
|
|
|
|
|
|||||||||||
|
(n |
|
|
|
|
2 |
(n |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
1) ln |
1) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
))ɢ |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
dx |
|
|
|
|
|
|
d(ln( x |
|
|
|
1 |
|
b |
|
|
|
|||||||||
|
|
(x |
|
) ln |
2 |
(x |
|
1) |
|
|
ln |
2 |
(x |
|
) |
b |
lim |
|
ln(x |
1) |
|
|
|
|
|||||
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
ɪ |
|
|
|
|
|
|
|
|
|
|
||||
|
|
blim |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
ln(b |
|
1) |
|
|
ɨ. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
ln 2 |
|
|
ln 2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Следовательно, данныйɬряд сходится. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
ɢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1.3. Знакопеременные ряды. Абсолютная и условная |
|
||||||||||||||||||||||||||
|
сходимость. Знакочередующиеся ряды. Признак Лейбница |
||||||||||||||||||||||||||||
|
|
|
|
ɡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
ɨ |
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
(1.7) |
|||||
|
|
Ряд |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|||||
|
ɩ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
называется знакопеременным, если среди его членов имеются как |
||||||||||||||||||||||||||||
|
положительные, так и отрицательные числа. |
|
|
|
|
|
|
||||||||||||||||||||||
ɟ |
Теорема 3. Достаточный признак сходимости ряда (1.7). |
|
|||||||||||||||||||||||||||
Ɋ |
|
|
|||||||||||||||||||||||||||
|
Если ряд |
|
|
|
|
|
|
|
|
|
n |
1 |
n | , |
|
|
|
|
|
|
|
(1.8) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
составленный из модулей членов ряда (1.7), сходится, то ряд (1.7) |
||||||||||||||||||||||||||||
|
также сходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
Ряд (1.7) называется абсолютно сходящимся, если сходится |
|||||||||||||||||||||||||||
|
ряд (1.8). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
10
