
Математика№3
.pdf
Получили знакочередующийся ряд. Третий член по модулю меньше заданной точности. Значит, достаточно взять два слагае-
1/4
мых:
0
sin x |
dx |
,25000 ,00087 ,24913 . |
|
x |
|||
|
|
|
|
3. Интегрирование |
|
|
|
дифференциальных |
|
уравнений |
||||||||||||||||||||||||||
с помощью рядов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Многие дифференциальные уравнения не приводятся к квад- |
||||||||||||||||||||||||||||||||
ратурам, а их решения не выражаются в элементарных функциях. |
||||||||||||||||||||||||||||||||||
Решения некоторых из этих уравнений могут быть представлены |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɍ |
в виде степенных рядов, сходящихся в определенных интервалах. |
||||||||||||||||||||||||||||||||||
В таких случаях ряд, являющийся решением дифференциального |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɍ |
|
уравнения, можно найти или способом неопределенных коэффи- |
||||||||||||||||||||||||||||||||||
циентов, или способом, основанным на применении ряда Тейлора. |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɇ |
|||
|
|
Пример 5. Найти в виде степенного ряда решение диффе- |
||||||||||||||||||||||||||||||||
ренциального |
уравнения |
y |
|
xy |
|
, |
удовлетворяющее |
началь- |
||||||||||||||||||||||||||
ным условиям y(0)=1, |
y (0) |
0 . |
|
|
|
|
|
|
|
|
|
Ȼ |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
Решение. Первый способ. Применим метод неопределенных |
||||||||||||||||||||||||||||||||
коэффициентов. |
|
|
Записываем |
|
|
искомоеɣрешение в виде ряда |
||||||||||||||||||||||||||||
y |
C |
0 |
1 |
x |
|
2 |
x 2 |
3 |
x 3 |
C |
4 |
x 4 |
|
5 |
x 5 |
|
... . |
Находим |
произ- |
|||||||||||||||
водные: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɢ |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
y C 2C |
|
|
x 3C |
|
|
x |
2 |
|
|
|
|
3 |
|
|
C |
|
|
x |
4 |
..., |
|
|
|
|||||||||
|
|
2 |
3 |
ɪ4C x |
|
|
|
5 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
y |
|
C |
2 |
2 3C |
x |
|
|
|
4C |
4 |
x2 |
|
4 |
|
5C |
5 |
x3 |
6C |
6 |
x4 ... . |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3ɨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Подставляя y и y в данное уравнение, получаем: |
|
|
|
|||||||||||||||||||||||||||||
2C2 |
|
|
2 3C3 x |
ɬ |
4 |
5C5 x 3 |
5 6C6 x 4 . . . |
|
|
|
||||||||||||||||||||||||
|
|
|
4C4 x 2 |
|
|
|
. |
|
||||||||||||||||||||||||||
|
|
x C |
|
x 2 |
C |
|
|
x 3 |
|
|
x 4 |
|
|
|
x 5 |
|
|
|
x 6 |
|
|
|
|
|
x 7 . . . . |
|
||||||||
|
0 |
1 |
2 |
3 |
|
|
4 |
|
5 |
|
|
|
|
6 |
|
|
||||||||||||||||||
Приравнявɡкоэффициенты при одинаковых степенях x в обеих |
||||||||||||||||||||||||||||||||||
частях последнего уравнения, получим систему: |
|
|
|
|||||||||||||||||||||||||||||||
ɨ |
|
|
|
|
|
|
|
|
2C2 |
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
ɩ |
|
|
|
|
|
|
|
|
|
|
|
2 |
3C3 |
|
|
C0 , |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
4C4 |
|
|
C1 , |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ɟ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
5C5 |
|
|
C2 , |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ɋ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
6C6 |
|
|
C3 , |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
7C7 |
|
|
C4 , |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.......... ....... |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Используя начальные условия, |
|
|
из выражений для y и y находим: |
|||||||||||||||||||||||||||||||
y(0) |
|
|
|
|
0 , |
C0 |
|
|
|
, y (0) |
|
|
|
|
1, |
C1 |
|
|
. Решая систему, полу- |
|||||||||||||||
21

|
чаем C2 |
, |
C3 |
|
1 |
|
, |
C4 |
, |
C5 |
|
|
, C6 |
|
|
|
1 |
|
, |
C7 |
|
, . . . . |
|||||||||||
|
|
|
|
|
|
|
|
2 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 3 5 6 |
|
|
|
|
|
|
|||
|
|
|
Таким образом, искомое решение представляется следую- |
||||||||||||||||||||||||||||||
|
щим |
|
рядом: |
y |
1 |
|
1 |
x 3 |
|
1 |
|
|
x 6 |
|
|
... . |
Этот ряд сходится |
||||||||||||||||
|
|
|
|
|
|
|
|
2 3 |
|
|
|
2 3 5 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
при всех значениях x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Второй способ. Применим для исходного уравнения метод |
||||||||||||||||||||||||||||||
|
последовательных дифференцирований. |
|
|
Решение |
y(x) |
ищем в |
|||||||||||||||||||||||||||
|
виде y(x) |
y(0) |
|
y (0) x |
|
|
y (0) x2 |
|
|
|
|
|
y(n) (0) xn |
|
|
. |
|
|
ɍ |
||||||||||||||
|
|
|
|
|
|
|
|
1! |
|
|
|
|
2! |
|
|
|
|
|
|
|
|
|
n! |
|
|
|
, yɌ(0) |
|
|||||
|
|
|
В соответствии с начальными условиями y(0) |
|
. |
||||||||||||||||||||||||||||
|
Подставляя |
|
в уравнение |
|
x |
0, y |
|
1 , |
получим |
y (0) |
|
1 |
|
; |
|||||||||||||||||||
|
y (0) |
. Для получения значений остальных производныхɇ |
бу- |
||||||||||||||||||||||||||||||
|
дем последовательно дифференцировать исходное уравнение: |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
y |
|
|
|
y , y |
(4) |
|
|
|
|
y |
|
|
|
Ȼ |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 y |
y , |
|
|
|
|
|
||||||||||
|
|
|
|
y(5) |
|
3 y |
|
xy , |
|
|
, |
y(n) |
|
(n |
|
|
).y(n |
3) |
xy(n 2) , |
|
|
|
|
||||||||||
|
|
|
Отсюда |
получим |
|
|
|
y(n) (0) |
|
ɣ |
3) (0) . |
|
Тогда |
|
при |
||||||||||||||||||
|
|
|
|
|
|
|
n |
|
|
y(n |
|
|
|
||||||||||||||||||||
|
n |
|
,4,5, |
имеем: |
|
|
|
|
|
|
ɢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
y (0) |
|
1, y(4) (0) |
|
|
, y(5) (0) |
|
|
, y(6) (0) |
|
4, y(7) (0) |
0, |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
y(8) |
(0) |
ɪ |
|
|
4 |
|
7 . |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
0, y |
(9) |
(0) |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
ɨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y(x) , |
|||||||
|
|
|
Подставляя найденные значения в степенной ряд для |
||||||||||||||||||||||||||||||
|
получим |
|
|
ɬ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
ɢ |
|
1 |
|
|
|
4 |
|
|
|
4 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
3 |
|
6 |
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
3! x |
|
6! x |
|
|
|
9! |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
y |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
ɡ |
x3 |
|
|
|
|
x6 |
|
|
|
|
|
x9 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
ɨ |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
||||||||||
|
|
|
2 3 |
|
2 3 5 6 |
2 3 5 6 8 9 |
|
|
|
|
|
|
|||||||||||||||||||||
|
ɩ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
ɟ |
1.7. Ряд Фурье функции, заданной на отрезке длиной 2 |
|
|
||||||||||||||||||||||||||||||
|
1. Пусть функция f(x) определена и интегрируема на отрезке |
||||||||||||||||||||||||||||||||
Ɋ |
|
|
|||||||||||||||||||||||||||||||
[– |
, |
]. Рядом Фурье функции f(x) называется ряд |
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
a0 |
|
|
|
(an |
cos nx |
|
bn sin nx) , |
|
|
|
|
|
(1.16) |
|||||||||||||||
|
|
|
|
|
|
|
2 |
|
n |
1 |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

где
|
|
|
|
|
|
|
|
|
|
a0 |
|
|
|
1 |
|
f (x)dx, an |
|
|
1 |
|
|
f (x) cos nxdx, |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
(1.17) |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
bn |
|
|
|
f (x) sin nxdx, n |
|
1,2,3,... |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɍ |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
a0 , an , bn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
Числа |
|
называются коэффициентами Фурье функ- |
||||||||||||||||||||||||||||||||||||||||||||
|
ции f(x). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɍ |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
Теорема 7. Если функция f(x) кусочно-гладкая на отрезке [– , ], |
|||||||||||||||||||||||||||||||||||||||||||||
|
т.е. f(x) и ее производная f (x) – непрерывны на отрезке [– |
, ] или |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɇ |
|
|
|
имеют на нем конечное число точек разрыва первого рода, то ряд |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
Фурье функции f(x) сходится в каждой точке отрезка [– , |
]. При |
||||||||||||||||||||||||||||||||||||||||||||||||
|
этом сумма S(x), x |
[– |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ȼ |
|
|
||||||||||||||||||||
|
|
|
], ряда Фурье (1.16) равна |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
f (x), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
если |
|
x |
|
|
точка |
непрерывности; |
||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɣ |
|
|
|
|
|
|
|
|||||||||
|
S(x) |
|
|
|
1 |
( f |
|
(x |
|
|
0) |
f |
(x |
|
|
|
0)), если x |
|
|
x |
|
|
точка разрыва f(x); |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( f (x |
|
|
0) |
|
f (x |
|
0)), |
|
если x |
|
|
|
|
|
|
или x . |
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
Здесь f (x0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɪ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
) |
|
|
x |
lim |
|
f (x), f (x0 |
|
0) |
|
|
|
x |
|
lim |
f (x) . |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xo |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
xo |
|
|
0 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(– |
,+ ) и |
|||||||||
|
|
|
|
Сумма S(x) ряда Фурье (1.16) определена для x |
||||||||||||||||||||||||||||||||||||||||||||||
|
является 2 – периодической функцией. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
Пример 1. Разложить функцию f(x)=e в ряд Фурье в интер- |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
ɢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
вале (– , ). Построитьɬграфик суммы ряда. |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Решение. Вычислим коэффициенты Фурье функции по фор- |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
ɡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
мулам (1.17), учитывая, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
ɨ |
e |
x |
sin |
xdx |
|
|
|
sin |
x |
|
|
|
cos |
x |
e |
|
x |
|
|
|
C, |
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
ɩ |
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
e x cos |
xdx |
|
|
|
cos |
x |
sin |
|
x |
e x |
|
|
|
C. |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ɋ |
Имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɟ |
1 |
|
|
|
x |
|
|
|
|
|
e |
e |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
a0 |
|
|
|
e |
|
dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sh |
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
an |
1 |
|
e x cos nxdx |
1 |
|
|
|
|
cos nx |
|
|
n sin nx |
e x |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
( |
1) n |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
(e |
|
|
|
cos n |
e cos |
|
n) |
|
|
|
|
(e e |
) |
|
||||||||||||||||||||||||||||
|
|
|
|
|
n2 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
n2 |
|
|
|
|
1 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
23
|
|
2sh |
|
|
|
( |
1) n |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
n2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
bn |
1 |
|
|
e x sin nxdx |
|
1 |
|
|
sin nx |
|
n cos nx |
e x |
|
|
1 |
|
|
( |
|
n) |
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
n2 1 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
(e |
|
cos |
|
n |
e |
|
cos |
|
n) |
1 |
|
( |
|
1) n 1 n |
(e |
|
|
e |
) |
|
|
|
|
|
|
ɍ |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n2 |
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
2sh |
|
|
|
( |
1) n |
1 n |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
n 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Поскольку функция ex и ее производная непрерывны на от- |
||||||||||||||||||||||||||||||||||||||||||||
|
резке [– |
, ], то по теореме 7 ряд Фурье этой функции сходитсяɌк |
||||||||||||||||||||||||||||||||||||||||||||||
|
самой функции ex на интервале (– , |
): |
|
|
|
|
|
|
|
|
ɇ |
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
x |
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
( |
|
1)n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
e |
|
|
|
|
|
sh |
|
|
|
|
sh |
|
|
|
|
|
|
|
|
|
|
|
|
(cos nx |
nsin x), |
|
|
x |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 n2 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ȼ |
|
|
|
||||||||||||||
|
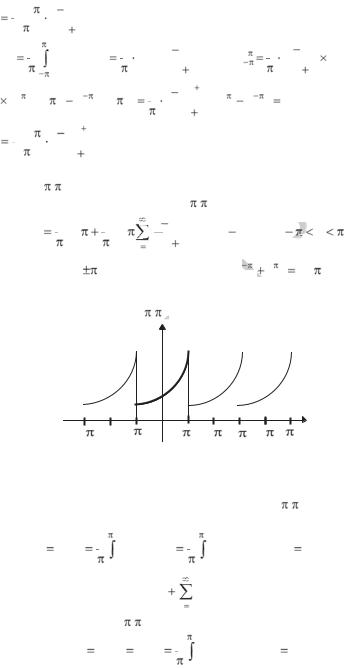
а в точках x= |
|
|
сумма ряда равна |
1 |
(e |
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
e ) |
|
ch . График |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
суммы ряда изображен на рис. 1.1 |
(пунктиром – |
график самой |
|||||||||||||||||||||||||||||||||||||||||||||
|
функции ex вне отрезка [– , |
|
|
]). |
|
|
|
|
ɣ |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
ɢ |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɪ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
ɬ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
-3 |
|
|
|
|
- |
0 |
|
|
|
|
|
|
|
2 |
|
|
3 |
|
|
4 |
|
5 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
ɢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
ɡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
ɨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
], то ее коэф- |
|||||||||||
|
|
|
2. Если f(x) – четная функция на отрезке [– |
|||||||||||||||||||||||||||||||||||||||||||||
|
фициенты Фурье находятся по формулам |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
ɟ bn |
|
0, a0 |
|
2 |
|
|
f (x)dx, an |
|
|
|
2 |
|
f (x) cos nxdx, n |
|
1,2,... , |
(1.18) |
||||||||||||||||||||||||||||||||
|
|
|
0 |
|
|
|
0 |
|
||||||||||||||||||||||||||||||||||||||||
Ɋ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
а ряд Фурье имеет вид: |
a0 |
|
|
|
|
|
an cos nx . Если f(x) – нечетная |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
n |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
функция на отрезке [– , |
|
], то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
a0 |
|
0, an |
0, bn |
|
|
|
2 |
|
|
f (x) sin nxdx, n |
|
1,2,... , |
(1.19) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24

а ряд Фурье имеет вид: |
bn sin nx . |
n |
1 |
|
|
Пример 2. Разложить в ряд Фурье функцию |
f (x) |
2 |
на |
||||||||||||||||||
отрезке [– , |
]. Построить график суммы ряда. |
|
|
|
|
|
|
||||||||||||||||
|
|
Решение. Поскольку функция четная, |
тоbn |
|
; a0 |
, an |
нахо- |
||||||||||||||||
дим по формулам (1.18), применяя интегрирование по частям: |
ɍ |
||||||||||||||||||||||
|
|||||||||||||||||||||||
|
|
a0 |
2 |
x 2 dx |
2 2 |
, |
|
|
|
|
|
|
|
|
|
|
|
Ɍ |
|||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
an |
2 |
x |
2 |
cos nxdx |
|
|
2 |
x 2 sin nx |
|
2 |
x sin nxdx |
|
|
|
|||||||
|
|
|
|
|
|
|
|
n |
|
0 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ȼ |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
= |
4 |
|
x cos nx |
|
|
1 |
cos nxdx |
|
|
|
|
ɇ |
|
|
|||||||
|
|
|
n |
|
|
|
n |
0 |
|
|
n |
0 |
|
ɣ |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
cos n |
|
|
|
|
|
|
|
|
|
4 . |
|
||||||
|
|
|
4 |
|
|
|
1 |
sin nx |
|
4 cos n |
( |
1)n |
|
||||||||||
|
|
|
|
|
|
|
n |
|
n2 |
|
ɢ |
|
|
|
|
|
n2 |
|
|
||||
|
|
|
|
|
|
|
|
|
0 |
|
n2 |
|
|
|
|
|
|
|
|||||
Согласно теореме 7, ряд Фурье данной функции |
f (x) |
|
2 |
на от- |
|||||||||||||||||||
резке [– |
, ] сходится к самой функции x2: |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
ɨ |
|
|
|
|
|
|
|
|
|
|
|
||||
x |
2 |
2 |
4 |
( |
|
1) |
n cos nx |
, |
ɪ |
|
(в точках x= |
сумма ря- |
|||||||||||
|
|
|
|
|
|
|
|
x |
|
||||||||||||||
|
|
3 |
|
n 1 |
|
ɬ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
да |
совпадает |
|
со |
значением |
функции |
|
f (x) |
2 , |
|
так |
как |
||||||||||||
2 |
|
|
ɢ2 |
|
|
|
) |
|
f ( |
) . На рис. 1.2 изобра- |
|||||||||||||
1 |
( f ( ) f ( |
|
|
1 |
( |
|
|
|
|
||||||||||||||
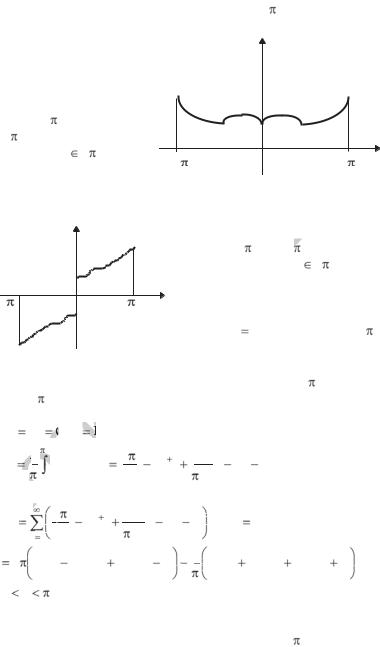
жен график суммы данного ряда (пунктиром – график самой |
|||||||||||||||||||||||
|
|
ɨ |
|
|
|
|
|
|
, |
]. |
|
|
|
|
|
|
|
|
|
|
|
||
функции x2 вне отрезка [– |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
ɩ |
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||
ɟ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɋ |
|
|
|
|
|
|
-2 |
- |
|
|
0 |
|
|
2 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Рис. 1.2
25
|
|
|
|
|
3. Если функция f(x) задана на отрезке [0, |
] и удовлетворяет |
||||||||||||||||
|
на нем условиям теоремы 7, то ее можно разложить в ряды Фурье |
|||||||||||||||||||||
|
различным образом, на- |
|
|
|
|
|
y |
|
|
|
||||||||||||
|
пример, как по косину- |
|
|
|
|
|
|
|
|
|
||||||||||||
|
сам, так и по синусам. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
В |
|
|
первом |
случае |
|
|
|
|
|
|
|
|
|
||||
|
продолжают f(x) с интер- |
|
|
|
|
|
|
|
|
ɍx |
||||||||||||
|
вала |
(0, |
) |
на |
интервал |
|
|
|
|
|
|
|
|
|||||||||
|
(– |
|
,0) |
|
четным |
образом: |
|
|
|
|
|
|
|
|
||||||||
|
f(x)=f(–x), |
x |
(– |
,0) |
(рис. |
|
- |
|
|
0 |
|
|
||||||||||
|
1.3), акоэффициентыФурье |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
Ɍ |
|||||||||||||
|
вычисляют |
по |
формулам |
|
|
|
|
Рис. 1.3 |
|
|||||||||||||
|
(1.18); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɇ |
|||||
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
во втором – продолжают f(x) с ин- |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
тервала (0, |
) на (– ,0) нечетным |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ȼ |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
образом: f(x)=–f(x), x (– ,0) (рис. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.4), а коэффициенты находят по |
||||||
|
- |
|
|
|
|
|
|
0 |
|
|
|
|
x |
|
формуламɣ(1.19). |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример3. |
Разложить функ- |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɢ |
2 |
на интервале (0, ) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
цию |
|
f (x) |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в ряд Фурье по синусам. |
|
|||||
|
|
|
|
|
|
|
|
Рис. 1.4 |
|
|
|
ɪ |
Решение. Продолжим функ- |
|||||||||
|
|
|
|
|
|
|
|
ɨ |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
цию x2 с интервала (0, ) на интер- |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
вал (– ,0) нечетным образом и вычисляем коэффициенты по |
|||||||||||||||||||||
|
формулам (1.19): ɬ |
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
a0 |
|
an |
|
, (n |
,2,...), |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
ɢ |
|
|
|
|
|
|
|
|
|
|
|
||
|
b |
|
|
|
2 |
|
x2 sin nxdx |
2 |
( |
|
1)n 1 |
4 |
|
(( 1)n |
1) . |
|
|
|||||
|
n |
|
|
|
|
ɡ |
|
n |
|
|
|
|
n3 |
|
|
|
|
|
||||
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Тогдаɨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
2 |
|
|
|
|
2 |
1) |
n 1 |
4 |
|
(( 1) |
n |
1) |
sin nx |
|
|
|
|
|||
|
ɩx |
|
|
n |
|
n3 |
|
|
|
|
|
|||||||||||
ɟ |
|
|
|
n |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
2 |
sin x |
sin 2x |
sin 3x |
|
|
8 |
sin x |
sin 3x |
sin 5x |
... , |
|||||||||||
Ɋ |
|
|
2 |
|
3 |
|
|
|
|
|
|
13 |
33 |
|
53 |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
0 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
(Сравните разложение этой же функции x2 в ряд по косину- |
|||||||||||||||||
|
сам, полученное в примере 2). |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
4. Если функция f(x) задана на отрезке [a,a+2 |
], то ее коэф- |
||||||||||||||||
|
фициенты Фурье вычисляются по формулам: |
|
|
|
||||||||||||||||||
26

|
|
1 a |
2 |
|
1 a |
2 |
|||
a0 |
|
|
|
a |
f (x)dx, an |
|
|
f (x) cos nxdx, |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
a |
|
bn |
|
1 a |
2 |
f (x) sin nxdx, n |
1,2,... . |
||||
|
|
|
|||||||
a
|
|
|
Пусть функция f(x) определена и интегрируема на отрезке |
|||||||||||||||||||||||
|
[–l,l]. Рядом Фурье функции f(x) называется ряд |
ɍ |
||||||||||||||||||||||||
|
|
|
|
|
|
a0 |
|
an cos |
|
|
nx |
|
|
bn sin |
nx |
|
, |
|
|
Ɍ |
||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
l |
|
l |
|
|
||||||||||
|
|
|
|
|
|
|
n |
1 |
|
|
|
|
|
|
|
|
|
ɇ |
||||||||
|
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a0 |
|
1 l |
f (x)dx, an |
1 l |
f (x) cos |
|
|
dx, |
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
l |
|
l l |
l |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
Ȼ |
|||||||
|
|
|
|
|
bn |
|
1 l |
f (x) sin |
|
|
|
|
dx, |
n 1,2, . . . . |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
l l |
|
|
|
|
|
ɣ |
|
|
|
||||||||
|
|
|
Если f(x) – кусочно-гладкая функция на отрезке [–l,l], то ее |
|||||||||||||||||||||||
|
ряд Фурье сходится в каждой точке отрезка [–l,l]. При этом сумма |
|||||||||||||||||||||||||
|
S(x), x [–l,l], ряда Фурье равна |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɪ |
|
|
|
|
|
|
|||||
|
|
|
|
f (x), |
|
ɨ |
|
|
если x |
точка непрерывности f (x); |
||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
S(x) |
|
|
( f (x0 |
0) f (x0 |
0)), |
|
если x |
x0 точка разрыва f (x); |
|||||||||||||||||
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
ɬ |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
( f |
( l |
0) |
f (l |
0)), |
|
|
|
если x |
l или x |
l. |
|||||||||||
|
|
|
|
2 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
ɢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
ɡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
Пример 1. Разложить в ряд Фурье по синусам функцию |
|||||||||||||||||||||||
|
|
ɨx, |
0 |
x |
1, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
f ( x) |
2 x, 1 x 2 . |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
ɩ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Решение. Продолжим f(x) на интервале (–2,0) нечетным об- |
|||||||||||||||||||||||
|
разом. Тогда a0 |
, |
an |
; при l=2 получаем: |
|
|||||||||||||||||||||
ɟ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɋ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
27

|
b |
n |
|
2 l |
f (x) sin |
nx |
dx |
l |
x sin |
nx |
dx |
2 |
(2 |
x) sin |
nx |
dx |
|
||||||||||||
|
|
l |
|
l |
|
|
2 |
|
2 |
|
|
||||||||||||||||||
|
|
|
0 |
|
|
|
|
|
|
0 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
8 |
|
sin |
n |
|
|
8( |
1)k |
|
|
, |
|
если |
n |
2k |
1, |
|
|
|
|
|
|||||
|
|
|
|
|
(2k |
1)2 |
|
2 |
|
|
|
|
|
|
|||||||||||||||
|
|
|
n |
2 |
2 |
2 |
|
|
|
если n 2k . |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɍ |
|||||||
|
|
|
|
Следовательно, разложение в ряд Фурье имеет вид: |
|
||||||||||||||||||||||||
|
|
|
|
f (x) |
|
8 |
|
|
( |
1) k |
|
sin |
(2k |
1) |
x |
, |
0 |
|
2 . |
|
|
|
|||||||
|
|
|
|
|
2 k |
0 |
(2k |
1) |
2 |
|
|
2 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ |
|
|
Ɍ |
|||||||||||||||||
|
|
|
|
|
|
|
ФУНКЦИЙ НЕСКОЛЬКИХ ПЕРЕМЕНЫХ |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɇ |
|
|||
|
|
|
|
|
|
|
|
|
2.1. Определенный интеграл по фигуре. |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Основные понятия и свойства |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ȼ |
|
|
|
|
|||
|
|
|
|
Пусть функция f(x,y,z) задана в точках тела W, на поверхно- |
|||||||||||||||||||||||||
|
сти тела Т или кривой Г в декартовойɣсистеме координат Oxyz. |
||||||||||||||||||||||||||||
|
Разобьем указанные фигуры на n частей |
|
Wi, |
Ti, |
Гi |
соответст- |
|||||||||||||||||||||||
|
венно и на каждой из частей выберем по одной точке (xi, yi, zi). |
||||||||||||||||||||||||||||
|
Меры полученных частей разбиения обозначим через |
|
|
Vi |
(обьем |
||||||||||||||||||||||||
|
части), |
Si (площадь части)ɪи Li (длина части) соответственно. |
|||||||||||||||||||||||||||
|
Через |
|
i |
|
обозначим наибольшее из расстояний между любыми |
||||||||||||||||||||||||
|
двумя точками, |
|
|
ɨ |
|
|
|
|
|
|
|
|
i |
1, n . |
Число |
||||||||||||||
|
взятыми на i-ой части разбиения, |
||||||||||||||||||||||||||||
|
|
|
|
max |
|
|
i , 1 |
ɬ |
|
|
|
|
насколько мелко разбиты фигу- |
||||||||||||||||
|
|
|
|
|
|
|
, показывает, |
||||||||||||||||||||||
|
ры, и называетсяɢдиаметром разбиения. |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
Составим теперь интегральные суммы: |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
ɡ |
|
|
W |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
ɨ |
|
|
|
|
|
f (x i , yi , zi ) Vi ; |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
n |
|
i 1 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
ɩ |
|
|
|
|
|
|
|
T |
|
f (x i , yi , zi ) Si ; |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
n |
i |
1 |
|
|
|
|
|
|
|
||||||||||||
ɟ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
Г |
|
n |
f (x i , yi , zi ) Li . |
|
|
|
|
|
|
|
|||||||||
Ɋ |
|
|
|
|
|
|
|
|
|
|
|
n |
i 1 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Если существуют конечные пределы этих интегральных |
||||||||||||||||||||||||||
сумм при |
|
|
0, причем эти пределы не зависят от способа раз- |
||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||
|
биения фигур и от выбора точек на частях разбиения, то они на- |
||||||||||||||||||||||||||||
|
зываются определенными интегралами функции f(x,y,z) по на- |
||||||||||||||||||||||||||||
|
званным фигурам: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
28

lim |
w |
n |
|
0 |
w |
|
f (x, y, z)dxdydz – тройной интеграл;
|
|
lim |
s |
f (x, y, z)ds – поверхностный интеграл I рода; |
|||||||||
|
|
n |
|||||||||||
|
|
0 |
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
lim |
Г |
f (x, y, z)dl – криволинейный интеграл I рода. |
|||||||||
|
|
n |
|||||||||||
|
|
0 |
|
Г |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Физический смысл интеграла по фигуре. |
|
|
|||||||||
|
|
Если f(x,y,z) – плотность распределения вещества по фигуре, |
|||||||||||
|
то интеграл по этой фигуре выражает ее массу в соответствую- |
||||||||||||
|
щих единицах измерения. |
|
|
|
|
|
|
ɍ |
|||||
|
|
Замечание. Аналогично названным вводятся интегралы: |
|||||||||||
|
|
f (x, y, z)dxdy |
– двойной интеграл по области D |
OxyɌ; |
|||||||||
|
|
D |
|
|
|
|
|
|
|
Ȼ |
|
||
|
|
f (x, y)dl |
– криволинейный интеграл I рода поɇкривой |
||||||||||
|
|
Г |
|
|
|
|
|
|
ɣ |
|
|
|
|
|
Г Oxy. |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Свойства интегралов по фигуре |
|
|
|
||||||||
|
(на примере тройного интеграла |
ɢ |
|
|
|
||||||||
|
|
f (x, y, z)dxdydz ). |
|
||||||||||
|
|
w |
|
|
|
|
|
v |
|
|
|
|
|
|
|
|
|
|
ɪ |
|
|
|
|
||||
|
|
1. Свойство линейности. |
|
|
|
|
|
|
|||||
|
|
( f (x, y, z) |
g(x, y, z))dxdydz |
|
|
|
|||||||
|
|
w |
|
|
ɨw |
|
g(x, y, z)dxdydz; |
и |
– числа. |
||||
|
|
|
|
ɬ |
|
|
|||||||
|
|
|
f (x, y, z)dxdydz |
|
|||||||||
|
|
|
ɢ |
|
|
|
|
|
|
|
|
||
|
|
2. Если область W есть объединение двух областей W1 и W2, |
|||||||||||
|
не имеющих общих внутренних точек, то |
|
|
|
|||||||||
|
|
ɡ |
f (x, y, z)dxdydz |
f (x, y, z)dxdydz. |
|||||||||
|
|
f (x, y, z)dxdydz |
|||||||||||
|
w |
ɨ |
|
|
w1 |
|
|
|
w2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
3. Если в области W: |
f (x, y, z) |
g(x, y, z) , то |
|
|
|||||||
|
ɩ |
|
|
g(x, y, z)dxdydz. |
|
|
|
||||||
ɟ |
f (x, y, z)dxdydz |
|
|
|
|||||||||
|
w |
|
|
|
w |
|
|
|
|
|
|
|
|
Ɋ |
|
4. Теорема о среднем. Если f(x,y,z) непрерывна в замкнутой |
|||||||||||
связной области W, |
то найдется точка (x*,y*,z*) |
W |
такая, что |
||||||||||
|
|||||||||||||
|
|
f (x, y, z)dxdydz |
f (x *, y*, z*) |
V , где V – объем тела W. |
|||||||||
|
w |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. Если f(x,y,z) |
1, то |
1dxdydz |
V . |
|
|
|
|||||
|
|
|
|
|
|
w |
|
|
|
|
|
|
|
|
|
Предполагается, что все указанные интегралы существуют. |
|||||||||||
29
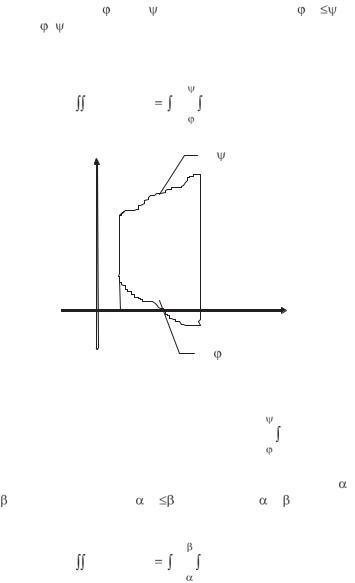
|
|
2.2. Вычисление двойных и тройных интегралов |
|
|
||||||||||||
|
|
|
|
|
в декартовых координатах |
|
|
|
|
|
||||||
|
|
а) Двойной интеграл. Пусть область D плоскости Oxyz огра- |
||||||||||||||
|
ничена линиями y= (x), |
y= (x), x=a, x=b, |
где a<b, |
(x) |
|
(x) и |
||||||||||
|
функции |
, |
непрерывны на отрезке [a; b] (рис.2.1). Двойной ин- |
|||||||||||||
|
теграл от непрерывной функции f(x,y) вычисляется путем сведе- |
|||||||||||||||
|
ния к двукратному интегралу по формуле |
|
|
|
|
|
|
ɍ |
||||||||
|
|
|
|
|
|
b |
( |
) |
|
|
|
|
|
|
||
|
|
|
|
|
f (x, y)dxdy |
dx |
f (x, y)dy. |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
(2.1) |
||||||||
|
|
|
|
D |
|
a |
(x ) |
|
|
|
|
Ɍ |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
y |
|
|
|
y= (x) |
|
|
|
ɇ |
|
|
||
|
|
|
|
|
|
|
ɣ |
Ȼ |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
y D |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
yxxa |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
xDɢ |
|
|
|
|
|
|
|
|||
|
|
|
|
0 |
a |
ɪ |
b |
|
|
x |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
ɨ |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
ɬ |
|
|
y= (x) |
|
|
|
|
|
|
|
||
|
|
|
|
ɢ |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
Рис. 2.1 |
|
|
|
|
|
|
|
|
||||
|
|
ɡ |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
ɨВ выражении (2.1) |
|
|
|
|
|
( |
) |
|
|
|
||||
|
|
сначала вычисляется |
|
f (x, y)dy |
при |
|||||||||||
|
ɩ |
|
|
|
|
|
|
|
|
(x ) |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
постоянном x. Полученный результат интегрируется по x. |
|
|
|||||||||||||
ɟ |
Аналогично, |
если область D ограничена линиями x= (y), |
||||||||||||||
(y), y=c, y=d, где c<d, |
(y) |
(y) и функции |
и |
непрерывны |
||||||||||||
Ɋ |
x= |
|||||||||||||||
на отрезке [c; d] (рис.2.2), то |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
d |
( y) |
|
|
|
|
|
|
|
|||
|
|
|
|
|
f (x, y)dxdy |
dy |
f (x, y)dx. |
|
|
|
(2.2) |
|||||
|
|
|
|
D |
|
c |
( y) |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
30 |
|
|
|
|
|
|
|
|
||
