Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Белорусский национальный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Математика№3

.pdf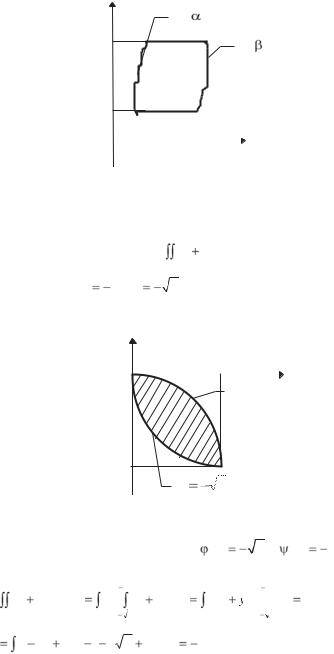

Скачиваний:

Добавлен:

31.05.2015

Размер:

5.81 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 84 5 6 7 8 > Следующая >>>

x= (y)

Рис. 2.2

Замечание. В более общем случае область интегрирования

разбивают на части, каждая из которых имеет один из рассмот-

ренных видов.

Пример 1.

Вычислить

2y)dxdy

, где область ограни-

чена линиями y

x2, y

x .

Решение. Указанные линии пересекаются в точках О(0,0) и

А(1,–1) (рис. 2.3).

y=-x

-1

Рис. 2.3

Применяя формулу (2.1) при

(x)

x ,

(x) 2 , a=0,

b=1, получим:

x 2

(x 2y)dxdy

dx (x 2y)dy

(xy

)

(( 3

4 )

(

))dx

Пример 2. Изменить порядок интегрирования в двукратном

интеграле

f (x, y)dy .

x 2

Решение. Область интегрирования, ограниченную линиями

2 ,

2x ,

x=2 (рис. 2.4), разобьем с помощью пря-

мой y=1 на три области. Получим сумму интегралов:

2 x

f (x, y)dy

f (x, y)dx

2 x x2

y2 / 2

1 1 y2

f (x, y)dx.

y2 / 2

Рис. 2.4

Здесь для определения пределов изменения переменной x

уравнения

разрешены

относительно

x 1 1 y2

, x y2 / 2 .

Из свойств интеграла по фигуре следует, что площадь S пло-

скойɨобласти D в декартовых прямоугольных координатах равна

dxdy .

(2.3)

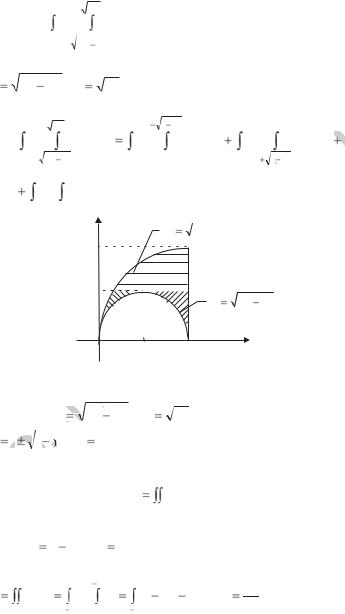
Пример 3. Вычислить площадь области,

ограниченной ли-

x2, y3

2 .

ниями y

Решение. Имеем (рис. 2.5)

dxdy

x 2

2/3 )dx

32 .

x 2/3

Рис. 2.5

y
2
1	y3	x 2
1
	y	2 x 2
-1 0	1	x

Геометрический смысл двойного интеграла: объем VɌцилинɍ- дрического тела, ограниченного сверху непрерывной поверхностью z=f(x,y), (f>0), снизу плоскостью z=0 и с боков прямой цилиндрической поверхностью, вырезающей на плоскости Oxy об-

ласть D, вычисляется по формуле

f (x, y)dxdy .

ɇ(2.4)

ɣz

Площадь S гладкой поверхности z=z(x,y), проектирующейся

в область D плоскости Oxy, выражается формулой

dxdy .

(2.5)

б) Тройной интеграл. Пусть пространственная область V в

декартовой системе координат Oxyz ограничена снизу и сверху

поверхностями z=F(x,y), z=

(x,y)

(F(x,y)

(x,y)), с боков прямой

цилиндрической поверхностью и проектируется на плоскость Oxy

в область D, ограниченную линиями y=

(x), y= (x),

x=a, x=b,

ɢ z

, – непрерывны (рис.2.6).

(a<b, (x) (x)), а функции F, ,

z=Ф(x,y)

z=F(x,y)

(x)	y
(x)
(x)
Рис. 2.6

Тройной интеграл от непрерывной функции f(x,y,z) вычисля-

ется по формулам:

(

, y)

f (x, y, z)dxdydz

dxdy

f (x, y, z)dz

F(x, y)

( )

(

, y)

f (x, y, z)dz .

(x)

F(x, y)

Замечание. Порядок интегрирования в последней формуле

может быть изменен.

Пример4. Вычислить тройной интеграл

ɇ3 dxdydz ,

где область V ограничена поверхностями x+y+z=1, x=0, y=0, z=0.

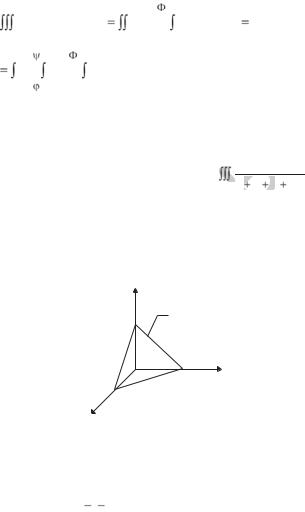
Решение. Область V есть пирамида, ограниченная снизу

плоскостью z=0, сверху плоскостью x+y+z=1 и с боков плоско-

стями x=0, y=0 (рис.2.7). Проекцией пирамиды на плоскость Oxy

является треугольник, ограниченный прямыми x=0, y=0, x+y=1.

ɪx+y+z=1

Рис. 2.7

ɩДля переменной z нижним пределом будет z=0 (плоскость

Oxy), а верхним – значение z, полученное из уравнения плоскости

ɟx+y+z=1, то есть z=1

y. Поэтомуполучим:

z)3 dxdydz

0 dx

V (1

z)3

1 1

2 0

(1 x y z)2

z 0

1 1

1 x

1 1

y 1 x

2 0

4 (1 x y)

2 0

4 1 x y

y 0

1 1 x 1

1 3 x

ln | 1 x |

1 ln 2

5 .

2 0

2 1 x

2 4

Из свойств интеграла по фигуре следует, что объем V пространст-

венной области V равен

dxdydz .

(2.6)

Пример 5. Вычислить объем тела, ограниченного поверхно-

стями

ɣx , y x .

Решение. Тело V ограничено снизу и сверху параболоидами

вращения

2 ,

цилиндрической

2y2

с боков –

поверхностью y

(рис.2.8). Проекция

и плоскостью

этого тела на плоскость Oxy есть область, ограниченная линиями

y x2 , y x , (0 x 1).

y=x2

y=x

Рис. 2.8

Имеем

dxdydz

2x 2

2 y2

x 2

(x 2

2 )dy

x 2

2.3. Замена переменных в кратном интеграле

а) Замена переменных в двойном интеграле. Если в двой-

ном интеграле

f (x, y)dxdy

осуществляется замена переменных

с помощью функций

(2.7)

x=x(u,v), y=y(u,v),

которые отображают взаимно-однозначно область G плоскости

Ouv на область D плоскости Oxy, то

f (x, y)dxdy

J (u, v)

dudv ,

(2.8)

f (x(u, v); y(u, v))

где

– якобиан.

(2.9)

J (u, v)

Приɡэтом предполагается

, что функции (2.7) имеют непре-

рывные частные производные по аргументам u, v и якобиан (2.9)

отличен от нуля. В частности, при переходе к полярным коорди-

натам

где x=

cos

sin

якобиан |J(

)|=

и формула

(2.8) имеет вид:

f (x, y)dxdy

f ( cos

, sin

)

d d .

(2.10)

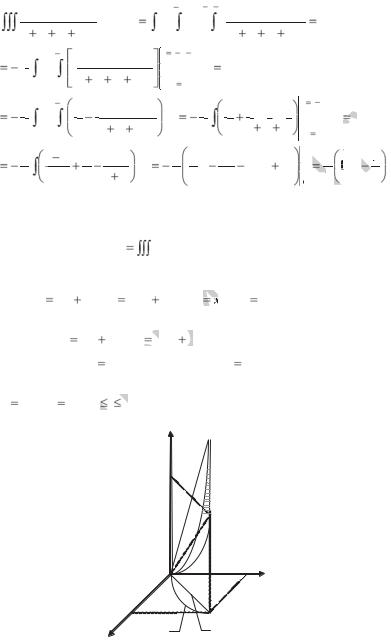
Если область D ограничена лучами, образующими с поляр-

ной осью углы

и кривыми

= 1(

)

), где

1< 2,

1< 2 (рис. 2.9), то

2 (

)

d .

f (x, y)dxdy

f (

cos

sin

)

1 (

)

2 (

)

1 (

)

Рис. 2.9

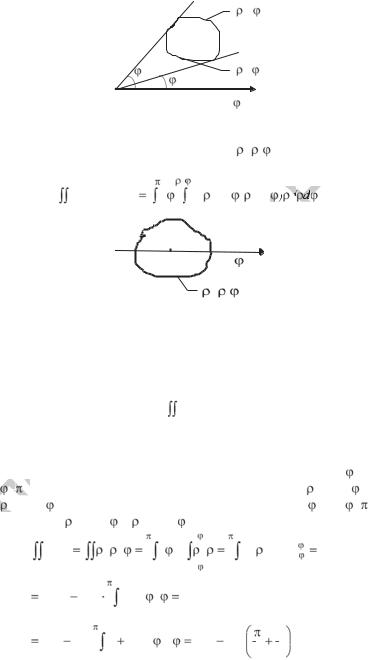
Если область D ограничена линией

(

) и начало коорди-

нат лежит внутри области (рис. 2.10), то

( )

f (x, y)dxdy

f ( cos , sin ) d

=0Ȼ

= (

)

Рис. 2.10

Если область интегрирования не удовлетворяет указанным

условиям, то для вычисленияɪдвойного интеграла надо предвари-

тельно разбить область на части, обладающие отмеченными выше

свойствами.

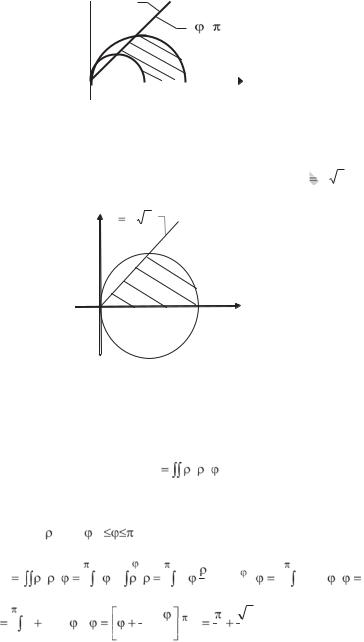
Пример 1.

Вычислить

dxdy , если область D ограничена

=2bx (a<b).

кривыми y=0,ɢx +y =2ax, y=x, x

Решение. Область D изображена на рис. 2.11. Уравнения

=0 и

прямых y=0 и y=x в полярной системе координат имеют вид

= /4. Уравнения окружностей соответственно

=2acos

=0 и

= /4

=2bcos . Итак, область D заключена между лучами

ɩи кривыми

=2acos

и =2bcos

. Тогда

dxdy

/ 4

2bcos

/ 4 1

2bcos

2a cos

0 2

/ 4

2(b2

a2 )

cos2

/ 4

a2 ) 1 cos2 )d

( b2 a2 )

y y=x

= /4

Рис. 2.11

Пример 2. Вычислить площадь плоской области D,

ограни-

ченной окружностью

x2+y2=2x

прямыми

y=0

Ɍy x 3

(рис. 2.12).

ɢ2

Рис. 2.12

Решение. Площадь плоской области D в полярной системе

координат вычисляется по следующей формуле:

d d .

Уравнение окружности в полярной системе координат запи-

шется в виде =2cos (0

/3). Тогда:

2cos

d d

cos

sin 2

0 /3

cos2

	б) Замена переменных в тройном интеграле.
	Если			x=x(u,v,w), y=y(u,v,w), z=z(u,v,w),							(2.11)
то				x=x(u,v,w), y=y(u,v,w), z=z(u,v,w),							(2.11)
то
		f (x, y, z)dxdydz									ɍ
	V
		f (x(u, v, w); y(u, v, w); z(u, v, w))\| J (u, v, w)\| dudvdw ,

										Ɍ
где		J (u, v, w)					– якобиан.		ɇ		(2.12)
									ɇ
							Ȼ
При этом предполагается, что функции (2.11) имеют непрерыв-
ные	частные		производные				по своимɣаргументам и			якобиан
J(u,v,w) отличен от нуля.							ɢ
							ɢ
	Формула преобразования тройного интеграла от декартовых
координат x,y,z к цилиндрическим координатам								,	, z (рис.2.13),
						ɪ
связанных с декартовыми соотношениями:
					z
					ɨ
			ɬ				М(x,y,z)
			ɬ
		ɢ					z
		ɢ
		ɡ					y
		ɡ					x
ɨ							x
					x		y
					x
ɩ						Рис. 2.13
ɟ		cos	,	0	< +
Ɋ		cos	,	0	< +
	y	sin	,	0		2	,
		,		-	< z < +
		,		-	< z < +
имеет вид:
		f (x, y, z)dxdydz					f ( cos , sin , ) d d d .				(2.13)
	V
							39

Пример 3. Вычислить массу тела, если его плотность в каж-

дой точке вычисляется по формуле		(x, y, z)	x 2	2 и тело V
ограничено параболоидом z	2	2 и	плоскостью z=4
(рис. 2.14).

			z															ɍ
			4												y			Ɍ
			4
																	ɇD
								z=x2+y2							2		ɇD
															2

	y		0			2		x		ɣ					Ȼ0			2 x
			0			2		x							Ȼ0			2 x
									ɢ
			а)						ɢ			б)
			а)				ɪ					б)
							ɪ
								Рис. 2.14
					ɨ
	Решение. Данная пространственная область V проектируется
в	область			D	ɬ			Oxy,		ограниченной							окружностью
в	область			D	плоскости			Oxy,		ограниченной							окружностью
x2	y2		4 . Вычислим тройной интеграл в цилиндрических ко-
				ɢ									z		2
ординатах. Уравнение параболоида будет													z		2 . Координаты ,
,	z		изменяются так:					0	2,	0	2	2	,			z	4;	плотность
	ɨ						2			2	2			2
	x	2	2		( cos	)	2	(	sin )	2		. Тогда масса M равна:
	x		ɡy		( cos	)		(	sin )			. Тогда масса M равна:
ɩ			M		(x, y, z)dxdydz					x			y		dxdydz
ɟ				V					V
Ɋ							2		2	4					2
					d d dz			d	2d dz 2						4			)d
							0		0	2					0
			2	4	5		2	2	32	32			128
			2	4	3			2	32	32			128
				3	5		0		3	5			15
							0

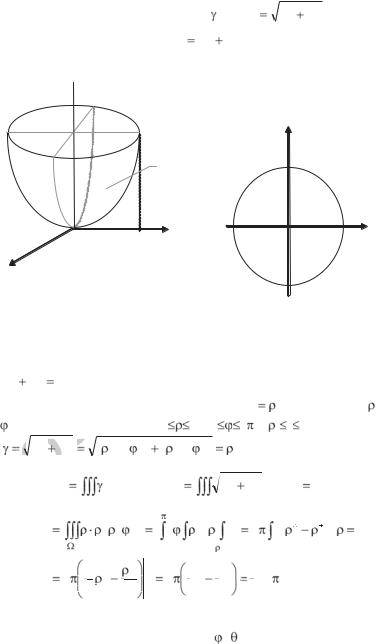
Формула преобразования тройного интеграла от декартовых координат x, y, z к сферическим r, , (рис.2.15), связанным с декартовыми соотношениями

<<< < Предыдущая 1 2 34 / 84 5 6 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
24.11.2019347.54 Кб7Математика шпоры 2.docx
#
31.05.20154.59 Mб81Математика Яцкевич, Раевская 2012.pdf
#
31.05.2015656.31 Кб9математика.pdf
#
31.05.2015376.18 Кб5Математика_2_Uslovia_KR_3.pdf
#
31.05.20155.47 Mб267Математика_практикум_Ч1.pdf
#
31.05.20155.81 Mб11Математика№3.pdf
#
14.04.2019124.58 Кб4материал к экзамену.docx
#
24.09.2019189.23 Кб13Материал печать 8 страниц на листе 1-59.docx
#
31.05.20152.29 Mб67Материал по философии.pdf
#
24.09.2019384.17 Кб5МАТЕРИАЛО.docx
#
21.09.20191.77 Mб4Материаловедение ПУЧКОВ 2011 шпоры.doc