
Математика№3
.pdf
Сходящийся знакопеременный ряд (1.7) называется условно сходящимся, если ряд (1.8) расходится.
Ряд вида
|
|
|
|
( |
1) n 1 u |
n |
|
|
u |
|
|
u |
|
|
|
|
u |
u ... |
( 1) n 1 u |
n |
..., |
(1.9) |
|||||||||||||||||||||||||||||
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
2 |
|
|
|
|
3 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
где un |
|
0, n |
|
|
12,,... , называется знакочередующимся. |
ɍ |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Признак Лейбница. Если члены знакочередующегося ряда |
||||||||||||||||||||||||||||||||||||||||||||||||
|
(1.9) удовлетворяют условиям: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
1) |
u1 |
u2 |
|
u3 |
|
|
|
... n |
|
|
|
un 1 |
... , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
2) |
lim un |
|
0 ,то ряд (1.9) сходится. Сумма его положительна и не |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
такого ряда имеетɌзнак |
|||||||||
|
превосходит первого члена u1 .Остаток rk |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
своего первого члена и не превосходит его по модулю: | rk | uk 1 . |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Примеры. Исследовать на абсолютную и условнуюɇсходи- |
||||||||||||||||||||||||||||||||||||||||||||||||
|
мость ряды: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin n |
ɣ |
Ȼ |
|
|||||||||||||||||||||
|
|
|
|
|
sin1 |
|
|
|
sin 2 |
|
sin 3 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
а) |
|
|
|
|
|
|
. |
|
|
. ; |
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
3 |
2 |
|
|
|
|
|
n |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɢ |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
б) 1 |
1 |
|
|
|
|
1 |
_ |
1 |
... |
|
|
|
|
( 1) |
n |
1 |
|
1 |
|
; |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
4 |
|
|
|
|
6 |
|
|
|
|
|
|
ɪ |
|
|
|
(2n) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
в) 1 |
1 |
|
|
|
|
1 |
... |
|
( ) n 1 |
|
|
1 |
... . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
ɨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
Решения. |
|
|
|
|
|
|
|
|
|
|
|
|
| sin1| |
|
| sin 2| |
|
| sin 3| |
|
|
|
|
|
| sin n| |
|
||||||||||||||||||||||||
|
|
|
а) Ряд из модулей |
|
|
|
|
|
|
. |
|
. схо- |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
ɢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22 |
|
|
|
32 |
|
|
|
1 |
|
n2 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɬ12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
дится по признаку сравнения, так как его члены не превосходят |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
ɡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Следователь- |
||||||||||
|
соответствующих членов сходящегося ряда |
n 1 |
|
n2 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
ɨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
но, исходный ряд сходится абсолютно. |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
ɟ |
|
б) Условия признака Лейбница здесь выполнены: ряд – зна- |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
, |
lim |
|
1 |
|
|
|
|
, n 1,2, ... . |
|||||||
|
кочередующийся, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
(2n)3 |
|
|
|
|
(2(n |
1))3 |
|
|
(2n)3 |
|
|
|
|||||||||||||||||||||||||||||||||||||
Ɋ |
ɩ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
||||||||||||||||||||||
Следовательно, |
|
|
|
этот |
|
|
|
ряд |
|
сходится. |
|
|
Ряд |
|
из |
модулей |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
также сходится, |
то есть исходный ряд схо- |
|||||||||||||||||||||||||||||||||
|
n 1 (2n)3 |
|
|
|
8 n 1 n3 |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
дится абсолютно. Найдем сумму данного ряда с точностью 0,01. Для этого возьмем столько его членов, чтобы следующий член ряда был по модулю меньше 0,01. Тогда остаток ряда, начинающийся с этого члена, будет по модулю также меньше 0,01.Модуль
11

|
четвертого члена |
1 |
|
1 |
,01 |
, поэтому с точностью 0,01 име- |
|||||||||||||||
|
|
|
|
|
|
|
|
63 |
|
216 |
|
|
|
|
|
|
|
|
|
|
|
|
ем: |
S |
1 |
1 |
|
|
1 |
1 |
1 |
1 |
57 |
0,89 . |
|
|
|
|
|
||||
|
2 |
3 |
|
|
43 |
8 |
64 |
64 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
в) Данный знакочередующийся ряд сходится по признаку |
|||||||||||||||||||
|
Лейбница, |
так |
|
как |
1 |
|
n |
1 , |
n |
1,2,3, . . . , lim |
1 |
. |
Этот |
ряд |
|||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
1 |
|
n |
|
n |
|
|
|
|
|
сходится условно, так как ряд |
, составленный из модулей |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
1 n |
|
|
|
|
|
|
ɍ |
|
членов данного ряда, расходится (гармонический ряд). |
|
|
||||||||||||||||||
|
|
Ɍ |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
1.4. Функциональные ряды. Область сходимости |
|
||||||||||||||||||
|
|
|
|
функционального ряда. Степенные ряды |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɇ |
|
||
|
|
Ряд |
вида |
|
u1(x) |
u2 (x) |
|
un (x) |
|
Ȼ |
|
|
|
||||||||
|
|
|
|
|
n |
un (x) , членами |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
которого являются функции un (x) , называется функциональным. |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɣ |
|
|
|
|
|
||
|
|
Множество всех действительных значений аргумента x, для |
|||||||||||||||||||
|
которых функциональный ряд |
ɢ |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n (x) |
|
|
|
|
|
(1.10) |
||
|
|
|
|
|
|
|
|
|
|
|
|
ɪ |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
становится сходящимся числовым рядом, называется областью |
||||||||||||||||||||
|
сходимости |
|
этого |
ɨ |
Функция |
S (x) |
lim S n (x) , |
где |
|||||||||||||
|
|
ряда. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
ɬ |
|
|
|
|
|
|
|
n |
|
|
|
||
|
S n (x) |
1 (x) |
|
|
|
un (x) , |
а |
x |
принадлежит |
области |
|||||||||||
|
|
|
2 (x) |
.. |
|
||||||||||||||||
|
сходимости, |
|
|
|
называется |
|
суммой |
|
ряда, |
|
функция |
||||||||||
|
Rn (x) |
S(x) |
|
S n (x) |
– остатком функционального ряда. |
|
|||||||||||||||
|
|
|
ɡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Для определения области сходимости ряда (1.10) можно ис- |
|||||||||||||||||||
|
пользовать известные признаки сходимости числовых рядов, счи- |
||||||||||||||||||||
|
|
ɨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
тая x фиксированным. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
ɩФункциональный ряд (1.10) называется равномерно сходя- |
||||||||||||||||||||
|
щимся на промежутке p |
|
R, если для любого |
> 0 |
существует |
||||||||||||||||
ɟномер n0, не зависящий от x, что для всех n > n0 и для всех x |
p |
||||||||||||||||||||
Ɋ |
выполняется неравенство |
| R n (x)| |
, то есть |
| S(x) |
|
S n (x)| |
, |
||||||||||||||
где Rn(x) – остаток ряда. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Признак |
|
Вейерштрасса. |
Если |un(x)| |
Cn, (n=1,2,...) |
при |
|||||||||||||||
|
|
|
|||||||||||||||||||
|
x |
[ ; b] и числовой ряд |
n |
C n |
сходится, |
то функциональный ряд |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
(1.10) сходится на отрезке [a, b] абсолютно и равномерно. |
|
|||||||||||||||||||
12

|
|
Теорема 4. Если члены сходящегося ряда (1.10) имеют не- |
||||||||||||||
|
прерывные производные |
при |
x |
[ ; b] |
и |
ряд из |
производных |
|||||||||
|
n 1 |
(x) |
сходится равномерно на [a, b], то ряд (1.10) можно диф- |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ференцировать почленно: |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
u (x) |
|
|
(x), x [ , b] . |
|
|
||||||
|
|
|
|
|
n 1 |
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
Теорема 5. Если члены ряда (1.10) непрерывны на [a, b] и |
||||||||||||||
|
этот |
ряд |
сходится равномерно |
на |
отрезке |
[a, b], |
то |
ряд (1.10) |
||||||||
|
можно |
|
|
|
|
|
|
|
|
|
|
|
|
|
ɍ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɍ |
||
|
интегрировать почленно: |
|
|
|
|
|
b |
|
|
|
|
|||||
|
|
|
|
b |
|
|
|
|
|
|
|
|
ɇ |
|||
|
|
|
|
|
un ( x) dx |
|
un ( x) dx . |
|||||||||
|
|
|
|
a |
n 1 |
|
|
|
|
|
n 1 a |
|
|
|||
|
|
Степенным рядом называется функциональный ряд вида |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Ȼ |
|
||
|
C n (x |
a) n |
0 |
1 (x |
|
a) |
2 (x |
|
a)2 |
.. . C n (x ) n .. . ,(1.11) |
||||||
|
n 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где Cn и a – действительные числа. ɣОбласть сходимости степен- |
|||||||||||||||
|
ного ряда (1.11) имеет один из следующих видов: |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
ɢ |
|
|
|
|
|
||
|
(a – R , a + R), [a – R , a + R), ( a – R , a + R], [a – R , a + R]. |
|||||||||||||||
|
|
Число R |
называется |
|
радиусом сходимости, а интервал |
|||||||||||
|
|
|
|
|
|
|
ɪ |
|
|
|
|
|
|
|
||
|
(a - R , a + R) – интервалом сходимости степенного ряда (1.11). |
|||||||||||||||
|
Радиус сходимости можно находить |
по формулам: |
|
|
||||||||||||
|
|
|
|
|
ɨ |
|
|
|
|
|
|
|
|
|||
|
|
|
|
R ɬlim |
1 |
|
, |
R |
|
lim |
Cn |
, |
|
|
|
|
|
|
|
|
n |
n | Cn | |
|
|
n |
Cn |
1 |
|
|
|
|||
|
если эти пределы существуют. В частных случаях R может быть |
|||||||||||||||
|
равен 0 или . |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
ɡ |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Вопрос о сходимости степенного ряда (1.11) в концевых |
||||||||||||||
|
точках области сходимости, |
то есть при x = a – R, x = a + R, ис- |
||||||||||||||
|
ɨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
следуется особо (с применением известных признаков сходимо- |
|||||||||||||||
|
ɩсти числовых рядов). |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Ряды, полученные почленным дифференцированием и ин- |
||||||||||||||
ɟтегрированием степенного ряда, имеют тот же радиус и интервал |
||||||||||||||||
Ɋ |
сходимости, и их сумма внутри интервала сходимости равна со- |
|||||||||||||||
ответственно производной и интегралу от суммы первоначально- |
||||||||||||||||
го ряда. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Пример 1. Найти область сходимости ряда |
|
1 |
1 n 2nx . |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
1 |
|
n |
|
|
Решение. |
При фиксированном x этот ряд – знакоположи- |
|||||||||||||
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
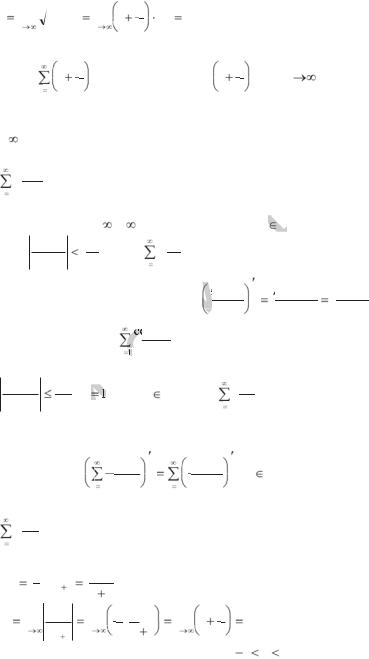
|
тельный. Применим |
|
|
к |
|
|
нему |
признак |
Коши. |
Найдем |
предел |
||||||||||||||
|
l |
lim n |
un (x) |
lim 1 |
|
|
1 |
2x |
2x ; |
l<1 |
– при |
2x < 1, |
т.е. при |
||||||||||||
|
|
|
n |
||||||||||||||||||||||
|
|
n |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
x < 0. При l = 1, т.е. при x = 0 данный функциональный ряд станет |
||||||||||||||||||||||||
|
рядом |
|
1 |
1 |
n |
. Общий член ряда |
1 |
1 n |
при n |
стремится |
|||||||||||||||
|
|
|
n |
1 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
к числу e, и поэтому ряд расходится (не выполнен необходимый |
||||||||||||||||||||||||
|
признак сходимости). Итак, область сходимости |
данного |
ряда |
||||||||||||||||||||||
|
(– |
, 0). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɍ |
|
|
|
|
Пример 2. |
|
Можно |
|
ли |
почленно |
дифференцировать |
||||||||||||||||
|
|
|
|
|
ряд |
||||||||||||||||||||
|
|
sin x |
|
в области его сходимости? |
|
|
|
|
Ɍ |
||||||||||||||||
|
n 1 |
n4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Областью сходимости данного рядаɇявляется вся |
||||||||||||||||||||||
|
числовая ось R=(– |
, + |
|
), так как для любого x |
R верно неравен- |
||||||||||||||||||||
|
ство |
sin nx |
|
1 |
, |
а ряд |
|
|
1 |
|
|
|
Ȼ |
|
|
||||||||||
|
|
n4 |
n4 |
|
n 1 |
n4 сходится. Члены исходного ряда |
|||||||||||||||||||
|
имеют непрерывные производные |
ɣ |
ncos nx |
cos nx , |
|||||||||||||||||||||
|
sin nx |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɢ4 |
|
|
n |
4 |
n |
3 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
||
|
ряд из производных |
|
|
cos nx |
сходится равномерно на R по при- |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
n |
|
1 |
|
|
n3ɪ |
|
|
|
|
|
|
|
||||
|
знаку |
|
Вейерштрасса. |
Действительно, верны неравенства |
|||||||||||||||||||||
|
cos nx |
|
1 |
|
|
|
|
ɨ |
|
|
|
1 |
|
|
|
|
|
||||||||
|
|
|
ɬ |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
n3 |
|
n3 , n |
x |
R |
, а ряд |
n 1 |
n3 |
сходится. По теоре- |
|||||||||||||||
|
|
|
12,, ... , |
|
|||||||||||||||||||||
|
ме 4 исходныйɢряд можно почленно дифференцировать в области |
||||||||||||||||||||||||
|
R его сходимости, т.е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
ɡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
ɨ n 1 |
sin nx |
|
|
|
sin nx |
, x |
R . |
|
|
|
|||||||||||||
|
|
n4 |
|
|
|
|
n 1 |
n4 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
ɩПример 3. |
|
Найти |
|
|
область |
сходимости |
степенного |
ряда |
||||||||||||||||
ɟ |
|
x n |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ɋ |
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Находим |
|
|
|
радиус |
|
сходимости |
ряда. |
||||||||||||||||
Cn |
|
1 |
, Cn |
1 |
|
1 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
n |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
R |
|
lim |
C n |
|
lim |
1 |
: |
|
|
1 |
|
lim |
1 |
1 |
1. |
Это |
означает, |
что |
||||||
|
|
C n |
|
n |
n |
|
1 |
|
n |
||||||||||||||||
|
|
|
n |
|
1 |
n |
|
|
|
|
|
n |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
исходный ряд сходится абсолютно при |
1 |
x |
1 . Далее, иссле- |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|

|
дуем сходимость ряда при x = 1. Если x = 1, то данный ряд ста- |
||||||||||||||||||||||||||||
|
новится |
гармоническим |
|
рядом |
|
|
1 |
, |
|
который |
|
расходится. |
|||||||||||||||||
|
|
|
|
x = –1, |
|
|
|
|
|
|
|
|
|
|
n |
1 |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
Если |
|
|
|
то |
|
получаем |
|
знакочередующийся |
ряд |
|||||||||||||||||||
|
1 |
1 |
|
1 |
... ( |
1) n 1 . .. |
, который сходится по признаку Лейб- |
||||||||||||||||||||||
|
|
2 |
|
3 |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ница. Следовательно, областью сходимости ряда является полу- |
||||||||||||||||||||||||||||
|
интервал [–1, 1). |
При |
|
1 |
|
x |
|
1 |
ряд |
сходится |
абсолютно, |
при |
|||||||||||||||||
|
x |
1 – условно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɍ |
||||
|
|
Пример 4. Найти сумму ряда |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɍ |
||||||||||||||||
|
|
|
|
|
|
|
x3 |
|
x4 |
|
|
x5 |
|
|
x6 |
... (| x | |
|
1) . |
|
|
|
||||||||
|
|
|
|
|
|
|
3 |
|
4 |
|
|
5 |
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Обозначим искомую сумму ряда через S(x), т.е. |
|
||||||||||||||||||||||||||
|
|
|
|
|
S(x) |
|
x 3 |
|
|
x 4 |
|
|
x 5 |
|
x 6 |
|
|
. |
|
|
ɇ |
|
|||||||
|
|
|
|
|
|
3 |
|
|
4 |
|
|
5 |
|
6 |
|
|
|
|
|
|
|
(1.12) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ȼ |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
сходится аб- |
|||||||
|
|
Можно проверить, что исходный ряд при |
|
x |
|
||||||||||||||||||||||||
|
солютно. Дифференцируем почленно равенство (1.12): |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɣ |
x |
2 |
|
|
|
|
|
|||||
|
|
|
|
|
S (x) |
|
x 2 |
|
x 3 |
|
|
x |
4 |
x |
5 ... |
|
|
, | x| |
1 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɢ |
|
|
|
1 |
|
x |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
(применена формула суммы членов убывающей геометрической |
||||||||||||||||||||||||||||
|
прогрессии). Отсюда, интегрируяɪи учитывая, что S(0)=0, находим |
||||||||||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
x |
t2 |
|
|
|
x |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
S(x) 0 |
|
|
ɨ |
|
|
|
|
|
|
|
|
|
|
t 1 dt |
|
|
|
||||||||
|
|
|
|
S (t)dt |
|
0 1 t |
|
dt |
0 |
|
t |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
x2 |
|
ɬ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
x ln | 1 |
|
x |, | x | 1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
ɢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 5. Найти сумму ряда |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
ɡ |
2x2 |
|
x3 x4 |
|
x5 |
.. ,| x | 1 . |
|
|
|
|
|
||||||||||||||
|
ɨРешение. Обозначим эту сумму ряда |
|
через S(x), |
т.е. |
|||||||||||||||||||||||||
|
S(x) |
|
2 x2 |
x3 |
|
x4 |
x5 .. . |
|
Данное |
равенство |
|
|
перепишем |
||||||||||||||||
|
ɩ |
|
|
|
|
|
|
|
|
|
|
|
|
|
3x 2 |
4x 3 |
|
5x 4 |
|
|
|
|
|
||||||
|
так: |
S(x)=x Q(x), |
где |
Q(x) |
2x |
|
|
|
. . |
|
Почленное |
||||||||||||||||||
ɟ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɋ |
интегрирование последнего равенства приводит к сумме членов |
||||||||||||||||||||||||||||
убывающей геометрической прогрессии: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
x |
|
|
|
x |
|
|
x |
|
|
|
|
x |
|
|
|
|
x |
|
|
|
|
|
|
||
|
|
|
|
Q(t)dt |
|
2tdt |
|
3t2dt |
|
4t3dt |
|
|
5t4dt ... |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
0 |
|
|
|
0 |
|
|
0 |
|
|
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
x |
3 |
x |
4 |
|
x |
5 |
|
... |
|
x2 |
x |
, | |
x | |
|
1 . |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||

|
|
|
Отсюда найдем Q(x): Q(x) |
|
|
|
x 2 |
|
|
|
|
1 |
|
|
|
|
1 |
|
|
, |
поэтому |
|||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
(x |
1)2 |
|||||||||||||||||||||||||||||||
|
искомая сумма S(x) такова: S(x) |
|
|
|
Q(x) |
|
|
|
|
|
|
|
|
x |
|
. |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
(x |
1)2 |
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
1.5. Разложение функции в ряд Тейлора |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
Если функция f(x) имеет производные всех порядков в окре- |
|||||||||||||||||||||||||||||||||||||||||||
|
стности точки x=a, то для нее можно написать ряд по степеням (x–ɍa): |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
f (a) |
|
|
|
|
|
|
|
|
|
f |
(a) |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
f ( n) |
(a) |
|
|
|
|
n |
|||||||
|
|
f (x) |
f (a) |
|
|
|
|
|
|
(x |
) |
|
|
|
|
|
|
|
(x |
|
|
|
) |
|
|
... |
|
|
|
|
|
|
(x |
Ɍa) . |
||||||||||||
|
1! |
|
|
|
|
|
|
2! |
|
|
|
|
|
|
|
|
|
n |
! |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ȼ |
|
|
|
|
|
||||||
|
|
|
f |
( n) (a) |
(x |
|
) |
n |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɇ |
|
||||||||
|
|
n 0 |
|
n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɣ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
x=a. |
Этот ряд называется рядом Тейлора функции f(x) в точке |
||||||||||||||||||||||||||||||||||||||||||||
|
Теорема 6. Если функция f(x) и все ее производные ограни- |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
чены на интервале (a–R, a+R) одним и тем же числом, т.е. суще- |
|||||||||||||||||||||||||||||||||||||||||||||
|
ствует |
постоянная |
|
|
M>0 |
|
ɪ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
такая,ɢчто выполняется неравенство |
||||||||||||||||||||||||||||||||||||||||||
|
|
f (n) (x) |
M , x |
|
(a |
|
|
|
R, a R), n |
|
,1,2,... , |
|
то функция f(x) пред- |
|||||||||||||||||||||||||||||||||
|
ставляется сходящимся к ней рядом Тейлора: |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɨ(n) |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(a) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
f (x) |
|
ɬn! |
|
|
|
|
(x ) |
|
, x ( |
|
|
|
R, a |
R) . |
|
(1.13) |
|||||||||||||||||||||||||
|
|
|
|
|
|
ɢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Равенство (1.13) |
верно и в случае, |
когда остаточный член |
|||||||||||||||||||||||||||||||||||||||||
|
|
ɨ |
|
|
|
(x) |
|
|
|
|
|
|
|
n |
|
f ( k ) (a) |
(x ) |
k |
|
|
стремится к нулю |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
n |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
ряда Тейлора R |
n |
f (x) |
|
k |
0 |
|
k ! |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
при n |
ɡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
. Остаточный член Rn(x) можно вычислить по формуле: |
||||||||||||||||||||||||||||||||||||||||||||
ɟ |
|
|
Rn (x) |
|
|
(x ) |
|
|
|
|
|
f ( n 1) [a |
|
|
|
x |
|
a)], |
|
0 |
|
1 . |
|
(1.14) |
||||||||||||||||||||||
|
|
|
|
|
(n 1)! |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
ɩ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Ɋ |
|
|
Если lim R n (x) |
0 , то ряд не сходится к данной функции. |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если в ряде Тейлора положим a=0, получим частный случай |
||||||||||||||||||||||||||||||||||||||||||||
ряда |
|
Тейлора, |
|
|
|
который |
|
|
называют |
|
|
|
рядом |
|
Маклорена: |
|||||||||||||||||||||||||||||||
|
f (x) |
f (0) |
|
|
(0) |
|
x |
|
|
f (0) |
x |
2 |
|
. |
|
|
f ( n) (0) |
|
x |
n |
. . |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
1! |
2! |
|
|
|
|
|
|
|
|
n! |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Приведем разложения в ряд Маклорена некоторых элементарных функций:
16
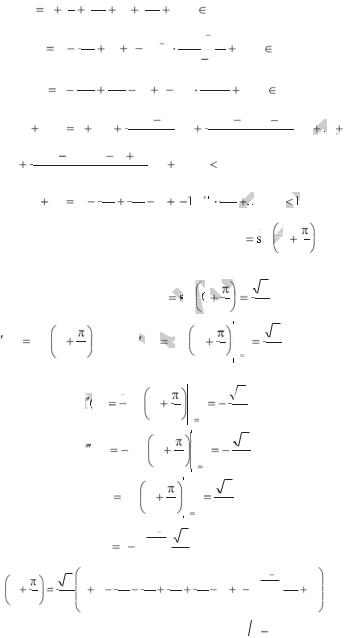
e |
x |
|
x |
|
x 2 |
|
|
... |
x n |
... ( x |
|
|
R); |
|
|
|
|
|
|
|
|
|
||||||||
|
|
1! |
|
|
2! |
|
|
n! |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
sin x |
x |
x |
3 |
|
... |
( 1) |
n 1 |
x 2n |
1 |
|
... (x |
|
R); |
|
|
|
||||||||||||||
3! |
|
|
|
(2n |
|
1)! |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
cos x |
1 |
x 2 |
|
x 4 |
... |
|
( |
1)n |
|
|
|
x 2n |
|
... (x |
R); |
|
|
ɍ |
||||||||||||
|
|
|
|
2! |
|
|
4! |
|
|
|
|
|
|
|
(2n)! |
|
|
|
|
|
|
|
|
|||||||
(1 |
x)m |
1 |
|
|
mx |
|
m(m |
|
) x 2 |
|
|
|
m(m |
|
1)(m |
|
) x3 ... |
|||||||||||||
|
|
m(m |
1)...( m |
|
|
n |
2! |
|
|
|
|
|
|
|
|
|
|
3! |
|
|
|
|
|
|||||||
|
|
|
|
) |
x n |
... (| x | |
1); |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
Ɍ |
|||||||||||||||||||
|
|
|
|
|
n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ln(1 |
x) |
x |
|
|
x 2 |
|
|
x 3 |
|
. . . |
( |
|
) |
n |
1 |
x n |
|
|
. . . |
(| x| 1) . |
||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
2 |
|
|
3 |
|
|
|
|
|
n |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɇ |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример 1. Разложить |
функцию |
|
|
f (x) |
|
sin |
x |
|
в |
ряд |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɣ |
|
Ȼ |
4 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Тейлора в окрестности точки x=0. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Решение. Имеем |
|
f (0) |
|
|
|
|
|
|
2 |
. |
|
Вычисляем |
||||||||||||||||||
|
|
sin 0 |
|
4 |
|
|
2 |
|
|
|||||||||||||||||||||
f (x) |
|
cos |
x |
4 |
|
, |
т.е. |
f (0) |
cos |
|
x |
|
|
4 |
|
|
|
|
2 |
. Далее после- |
||||||||||
|
|
|
|
|
|
|
|
|
ɪ |
|
|
|
|
x |
0 |
|
2 |
|
|
|
|
|||||||||
довательно получаем: |
ɨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
f |
|
ɬ |
x |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
(0) |
|
|
sin |
4 |
x |
|
0 |
|
|
2 |
|
, |
|
|
|
|
|
|
|||||||
|
|
|
ɢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 , |
|
|
|
|
|
|
|||||||
|
|
|
|
f |
|
(0) |
|
|
cos |
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
ɡ |
|
|
|
|
|
|
|
|
|
4 |
x |
|
0 |
|
|
2 |
|
|
|
|
|
|
|
|||||
ɨ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
IV |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||
ɩ |
|
|
|
f |
|
|
(0) |
|
sin |
x |
|
4 |
x |
|
0 |
|
|
2 . |
|
|
|
|
|
|
|
|
||||
ɟОтметим, что |
f ( n) (0) |
|
|
|
n2 n |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
( |
1) |
|
2 |
|
. Записываем ряд Тейлора: |
|
|||||||||||||||||||||||
Ɋ sin x |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1) n |
2 |
|
|
|
|
||
|
4 |
|
2 1 |
|
x |
|
|
x2 |
x3 |
|
x4 |
|
|
x5 |
|
.. |
( |
|
|
2 n |
xn |
|
. |
|
||||||
|
|
2 |
|
|
|
|
|
2! |
3! |
|
4! |
|
|
|
5! |
|
|
|
|
|
|
|
n! |
|
|
|
||||
Пример 2. Разложить функцию f (x) 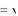 9 x 2 в ряд по степеням x, используя разложения основных элементарных функций.
9 x 2 в ряд по степеням x, используя разложения основных элементарных функций.
17
|
Воспользуемся приведенным выше биномиальным разложением |
|||||||||||||||||||||||||||
|
(1 |
|
x)m |
|
|
mx |
m(m |
|
|
1) |
x2 |
|
m(m |
1)(m |
|
) x3 |
... . |
(1.15) |
||||||||||
|
|
|
|
|
|
|
|
2! |
|
|
|
|
|
|
|
|
3! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
2 |
1 |
|
|
Преобразуем |
исходную |
функцию: |
|
|
|
9 |
x 2 |
1 |
2 |
|||||||||||||||||
|
|
|
|
|
|
. |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
Подставим в |
|
формулу |
(1.15) |
|
m |
|
|
1 , |
а |
вместо |
x выражение |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
ɍ |
|
x 2 |
. Получим следующее разложение: |
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
9 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
Ɍ |
|||
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
1 |
|
|
x2 |
2 |
|
ɇ |
|
|
|||||||
|
|
|
9 x2 |
|
|
1 |
|
|
2 2 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
2 |
|
9 |
|
|
2! |
|
|
|
|
9 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ȼ |
|
|
|
|||||||||||
|
|
|
1 |
1 |
1 |
... |
1 |
n |
1 |
|
|
|
|
n |
ɣ. |
|
|
|
||||||||||
|
|
|
|
|
x2 |
|
|
x2 |
|
|
|
|||||||||||||||||
|
|
|
2 |
2 |
2 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
n! |
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
2 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɢ |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
1 |
|
4 |
1 3 |
|
6 |
|
|
|
1 3 5... (2n |
|
3 ) |
|
2n |
|
|
|
||||||||
|
|
|
222!92 |
x |
|
233!93 |
x |
|
ɪ |
|
|
2n n!9n |
|
|
x |
|
|
. |
|
|
||||||||
|
|
|
|
|
|
|
|
ɨ |
2 |
1 |
, т.е. при |x|<3. |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
Разложение имеет место при |
x |
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
ɬ |
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
ɢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1.6. Применение степенных рядов в приближенных вычислениях |
|||||||||||||||||||||||||||
|
|
|
ɡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
1. Приближенное вычисление значений функций |
|
|
|
|||||||||||||||||||||||
|
ɨПусть функция f(x) в окрестности точки a разлагается в ряд |
|||||||||||||||||||||||||||
|
Тейлора. Тогда приближенное значение функции f(x) в любой |
|||||||||||||||||||||||||||
|
ɩ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
точке этой окрестности может быть вычислено как частичная |
|||||||||||||||||||||||||||
|
сумма этого ряда. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ɟ |
Пример 1. Вычислить 3 130 |
с точностью до 0,001. |
|
|
|
|||||||||||||||||||||||
Ɋ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
1 |
|
|
|
Решение. |
3 130 |
3 125 |
5 |
|
3 125 1 |
|
|
|
5 |
1 |
. Вос- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
25 |
|
|
|
|
25 |
|
|
|
|
|
пользуемся |
|
биномиальным |
|
|
|
рядом |
|
|
|
(1.15) |
|
|
при |
||||||||||||||
|
m |
1 |
, x |
1 |
|
( 1,1) . Получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
3 |
|
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|
|
2 |
1 |
1 |
|
1 |
1 |
|
|
|
|
|
|
3 ... |
|
|
|
|
|
|
3 130 |
|
5 1 |
1 |
|
1 |
|
|
3 |
3 |
|
1 |
3 |
3 |
|
3 |
|
|
|
|
1 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
25 |
|
|
2! |
|
|
25 |
|
|
|
|
3! |
|
|
|
|
25 |
|
|
|
||||
|
|
|
|
5 1 |
|
1 |
|
1 |
|
1 |
|
|
|
2 1 |
|
|
1 |
1 |
|
2 |
|
|
5 1 |
|
|
|
1 |
|
... |
|
||||||
|
|
|
|
|
3 |
25 |
|
3 |
|
|
|
3 2! |
252 |
3 |
|
3 |
|
|
3 3! |
|
253 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
5,0000 |
|
|
,0667 |
|
|
|
,0009 ... . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Полученный ряд является знакочередующимся рядом. Третий |
|||||||||||||||||||||||||||||||||||
|
член по модулю меньше 0,001, поэтому его и следующие за ним |
|||||||||||||||||||||||||||||||||||
|
члены |
|
можно |
|
отбросить. |
С |
указанной |
|
точностью |
|
|
|
ɍ |
|||||||||||||||||||||||
|
|
|
|
|
получим |
|||||||||||||||||||||||||||||||
|
3 130 ,0000 |
|
0,0667 |
,067 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɍ |
|||||||||||||||||
|
|
|
|
Пример 2. Вычислить e0,1 |
с точностью до 0,001. |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
Решение. Воспользуемся разложением |
|
|
|
|
|
ɇ |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
x |
1 |
|
|
x 2 |
x 3 |
. . . |
|
x n |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
, |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2! |
3! |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
x n |
1 |
|
|
|
|
|
|
|
|
|
|
|
Ȼn! |
|
|
|
|
|
|
||||||||
|
где |
R n |
|
|
|
e |
x |
, |
0 |
|
1, |
x |
R . |
При |
x=0,1 |
получаем: |
||||||||||||||||||||
|
(n |
|
1) ! |
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɣ |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
e |
0,1 |
1 |
|
0,1 |
|
(01, )2 |
|
(01, )3 |
|
. |
|
(01, ) n |
|
|
|
Определим, |
|
сколько |
|||||||||||||||||
|
|
|
|
|
|
|
2! |
|
|
|
3! |
|
|
ɢ. . |
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
надо |
слагаемых |
для |
|
достижения |
требуемой |
точности. |
|
Так как |
|||||||||||||||||||||||||||
|
0,1 |
[0,0,5], |
|
|
|
|
то |
|
|
|
0 |
ɪ |
|
Тогда |
|
|
|
e x |
|
|
0,5 |
2 ; |
||||||||||||||
|
|
|
|
|
|
|
|
|
x |
|
0,5 |
. |
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
n |
1 |
|
|
|
|
|
|
|
|
n |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R n |
x |
|
|
|
e x |
|
2x |
|
ɨ |
При |
x=0,1 |
|
имеем |
|
|
|
неравенство: |
||||||||||||||||||
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
(n |
|
1)! |
|
|
|
ɬ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
(n |
|
1)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
2 (01,) n |
|
1 |
|
|
,001ɢ. Полагая n=2, получим 2 0,001 |
|
|
|
,0003 |
,001 . |
|||||||||||||||||||||||||
|
|
(n |
) ! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|||
|
Значит, |
ɡ |
|
|
|
|
|
|
|
|
|
взять |
|
|
три |
|
|
|
|
слагаемых: |
||||||||||||||||
|
|
|
|
|
|
достаточно |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
e |
0,1 ɨ |
|
|
(0,1) |
2 |
|
|
|
,105 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
,1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
ɩ |
|
|
|
|
|
|
2! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
5 |
. |
|
|
|
|
|
|
|||||
ɟ |
|
|
Пример 3. Вычислить ln2 с точностью до |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
Решение. Применим разложение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
1 |
x |
|
|
|
|
|
|
x3 |
|
x5 |
|
x7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Ɋ |
ln |
|
2 |
x |
|
|
|
... . |
Этот |
ряд |
сходится |
при |
||||||||||||||||||||||||
1 |
x |
|
|
3 |
|
|
5 |
|
7 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
x |
|
(–1,1). Если |
1 |
|
x |
|
|
|
, то x=1/3. Возьмем n-ю частичную сумму |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ln 2 |
2 |
|
1 |
|
|
1 |
|
1 |
|
1 |
|
1 |
|
|
|
1 |
|
|
1 |
|
. Погрешность этого |
||||||||||||||
|
|
3 |
|
|
3 |
|
3 |
|
5 |
|
3 ... |
|
2n |
1 |
3 |
2n 1 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

равенства |
выражается |
остатком |
ряда |
Rn |
2 |
2n |
3 |
2n |
5 |
. Для его оценки все |
|
|
|
множители в знаменателях, стоящие перед степенью 3, заменим на 2n+3. Получим
|
|
|
|
|
Rn |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
1 |
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
ɍ |
||||||||||||||||||
|
|
|
|
|
|
(2n 3)32n 3 |
32 |
|
|
|
|
34 |
|
|
|
|
|
|
|
|
|
|
(2n 3)32n 3 |
|
1 |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ɍ |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
9 |
|
|
||
|
|
|
|
1 |
|
|
|
|
|
|
|
. |
|
|
|
Решая |
неравенство |
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
5 |
, нахо- |
||||||||||||||||||||||||||||||||||||||
|
|
4(2n |
)32n 1 |
|
|
|
|
|
4(2n |
3)3 |
2n |
1 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
дим, что n=4: |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
,000001 |
|
|
10 5 |
|
ɇ |
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. Итак, |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 11 39 |
|
|
866052 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ȼ |
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
ln 2 |
|
|
1 |
|
|
|
1 |
|
|
1 |
|
|
|
|
|
1 |
|
1 |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
3 |
|
|
|
3 |
|
33 |
|
|
|
|
|
5 |
35 |
|
7 |
37 |
|
|
|
|
9 |
|
39 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
,666667 |
|
|
|
|
,024691 |
|
|
|
,001646 |
|
|
,000131 |
|
|
0,000011 |
|
|
,69315 . |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
2. Приближенное вычисление определенныхɣ |
интегралов |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Если подынтегральная функция разлагается в степенной ряд, |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɪ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
а пределы интегрирования принадлежат области сходимости это- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
го ряда, то соответствующий определенный интеграл можно вы- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
числить с заданной точностью. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɬ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
Пример 4. Вычислитьɨинтеграл |
1/4 |
dx |
с точностью до |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
0,00001. |
|
|
|
|
|
ɢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
ɡ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на x, |
получим |
||||||||||||||||||
|
|
|
|
Решение. Разделив почленно ряд для sin x |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
ɨ |
|
x 3 |
|
|
x 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
sin x |
|
|
x |
|
|
3! |
|
|
|
5! |
|
|
|
. |
|
1 |
|
|
|
|
x |
2 |
|
|
|
|
|
|
x |
4 |
|
|
|
|
x |
6 |
|
|
|
|
. . Этот ряд сходит- |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
ɩ |
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3! 5! 7! |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
ся при x |
|
|
R. Интегрируем его почленно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
ɟ |
|
|
|
|
|
|
|
1/ 4 sin x |
|
|
|
|
|
1/ 4 |
|
|
|
|
|
|
|
x 2 |
|
|
|
|
x 4 |
|
|
|
|
|
|
x6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Ɋ |
|
|
|
|
|
|
|
0 |
|
|
x |
|
|
|
|
dx |
0 |
1 |
|
|
|
|
|
3! |
|
|
|
|
|
5! |
|
|
|
|
|
|
7! |
... |
dx |
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
x3 |
|
|
|
x5 |
|
|
|
|
|
|
x7 |
... |
|
1/ 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3! |
5 |
|
5! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
7! |
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
... |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
3 |
|
|
3! |
|
43 |
|
5 |
|
|
5! |
|
45 |
|
|
|
7 |
|
7! |
47 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
,25000 |
|
|
,00087 |
|
|
|
|
|
|
,0000016 .... |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
20
