
- •Министерство образования Республики Беларусь
- •Контрольная работа № 6.
- •Задание 6.11.
- •Задание 6.12.
- •Задание 6.13.
- •Задание 6.14.
- •Задание 6.15.
- •Контрольная работа № 7.
- •Задание 7.1.
- •Задание 7.2.
- •Задание 7.3.
- •Задание 7.4.
- •Задание 7.5.
- •Задание 7.6.
- •Задание 7.7.
- •Задание 7.8.
- •Задание 7.9.
- •Контрольная работа №8
- •Задание 8.1.
- •Задание 8.2.
- •Задание 8.3.
- •Задание 8.4.
- •Решение типового варианта
- •Задание 5.9. Найти общее решение:
- •Задание 5.10. Методом исключения найти общее решение системы:
- •Задание 5.11. А) Методом характеристического уравнения найти общее решение системы:
- •Решение типового варианта контрольной работы n6.
- •Решение типового варианта контрольной работы № 7
- •Решение типового варианта контрольной работы №8. Задача 8.1.
- •Задача 8.2.
- •Задача 8.3.
- •Задание 8.4.
- •С о д е р ж а н и е
- •Учебное издание
Задание 5.9. Найти общее решение:
![]()
Находим общее решение однородного уравнения:
![]()
![]()
![]()
Частное решение неоднородного уравнения по методу Лагранжа имеет вид:
![]()
Для нахождения функций
![]() составляем
систему:
составляем
систему:
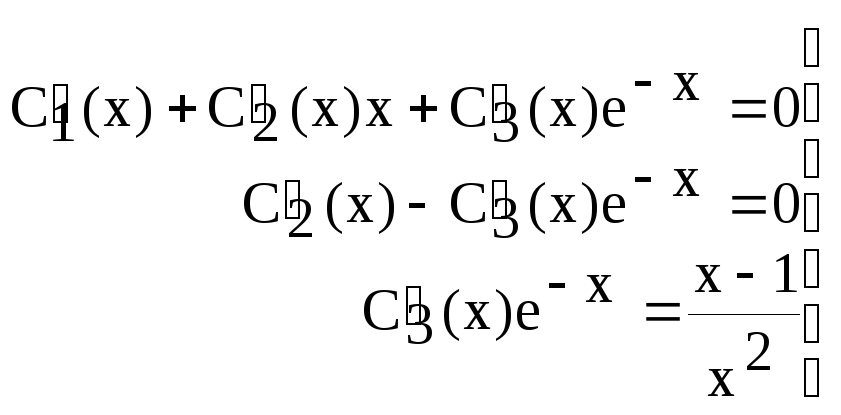
Тогда:
![]()
![]()
![]()
![]()
![]()
![]()
Таким образом, общим решением уравнения
является функция:
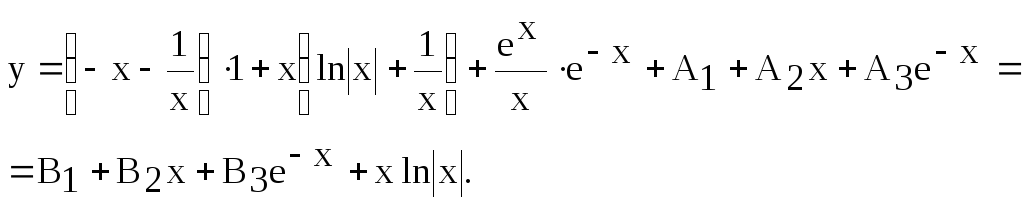
Здесь Ai, Bi(i =1, 2, 3).
Задание 5.10. Методом исключения найти общее решение системы:
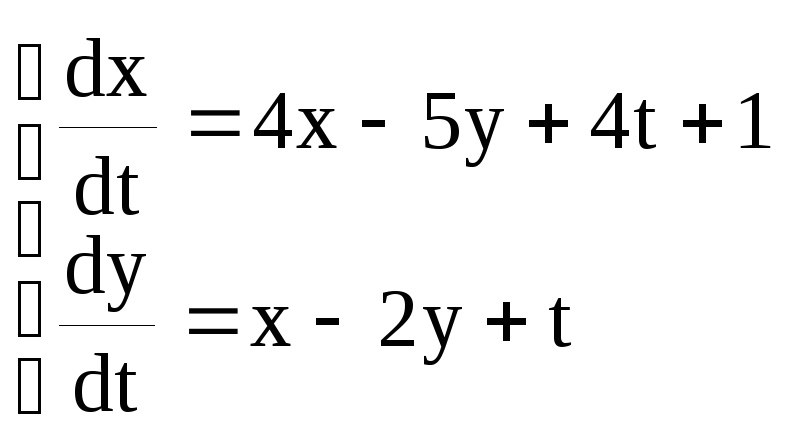
Первое уравнение продифференцируем по
![]() :
:
![]()
Из второго уравнения подставим в
полученное выражение
![]() :
:
![]()
Из первого выразим
![]() и подставим его в последнее уравнение:
и подставим его в последнее уравнение:
![]()
Окончательно получим:
![]()
Решаем это уравнение:
![]() ;
;![]()
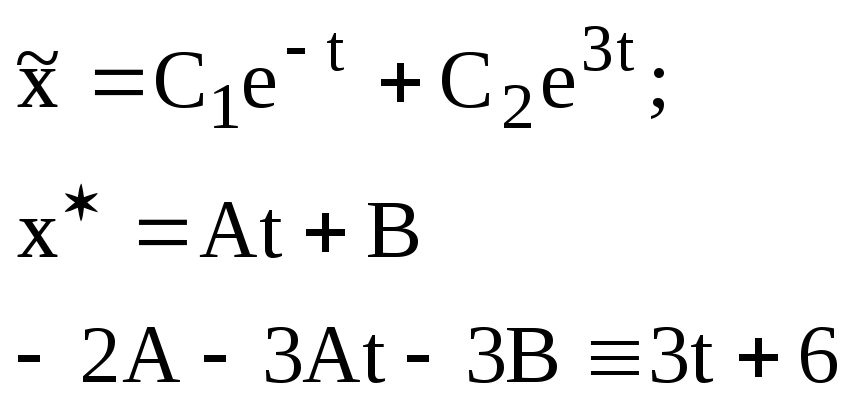
![]()
![]()
![]()
![]()
Из выражения для
![]() получим:
получим:
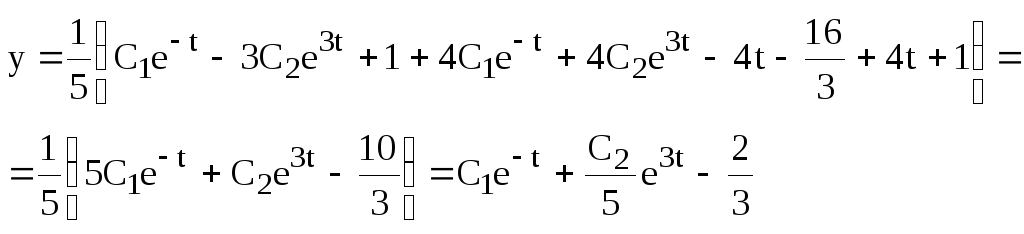
Таким образом, общее решение системы имеет вид:
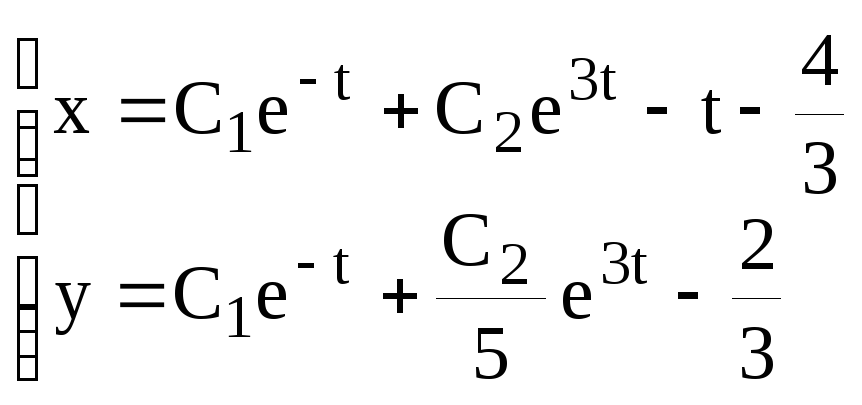 .
.
Задание 5.11. А) Методом характеристического уравнения найти общее решение системы:
![]()
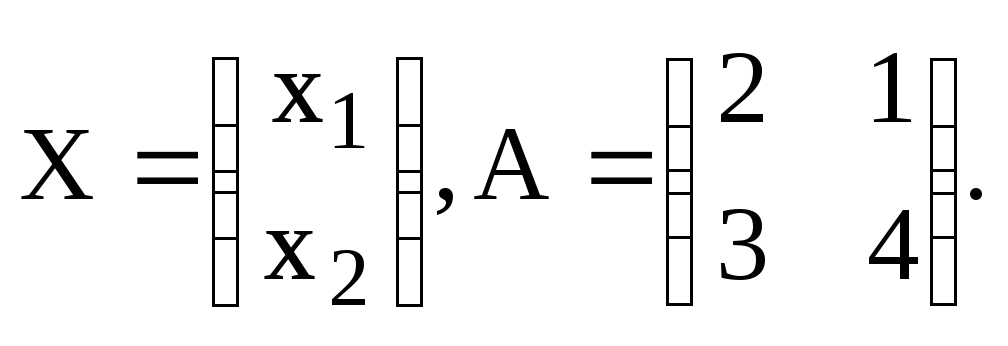
Составляем характеристическое уравнение и решаем его:
![]()
Для
![]() составляем систему:
составляем систему:
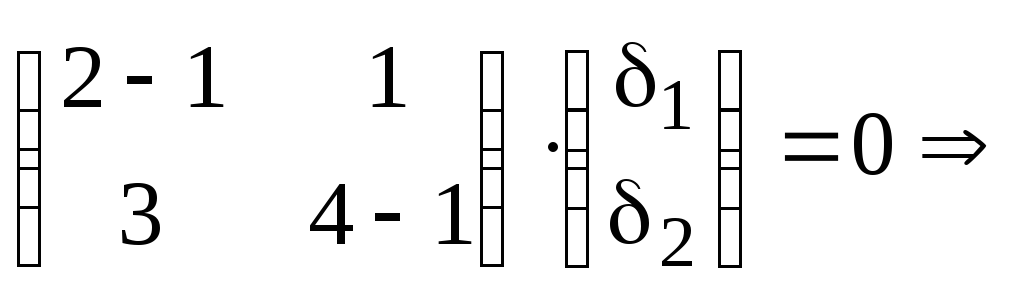
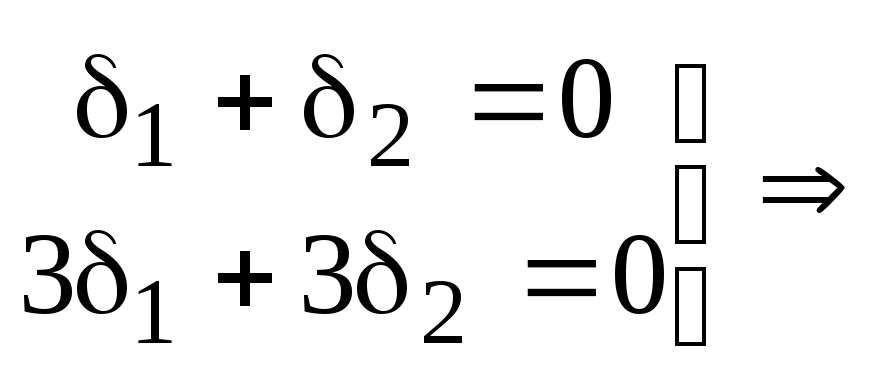
![]()
Пусть
![]() тогда
тогда![]() и
и
![]()
Для
![]() :
:
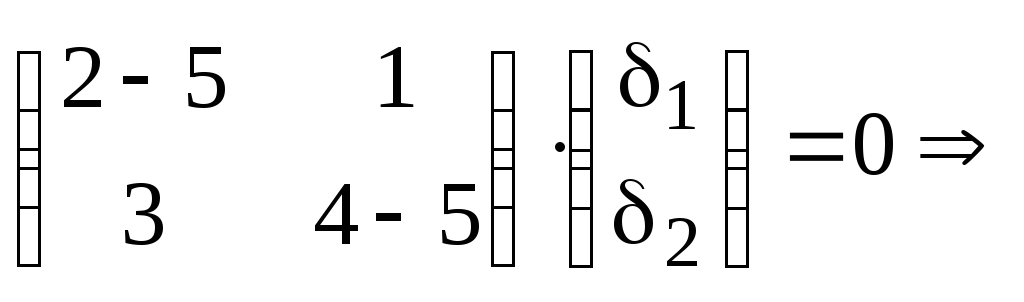
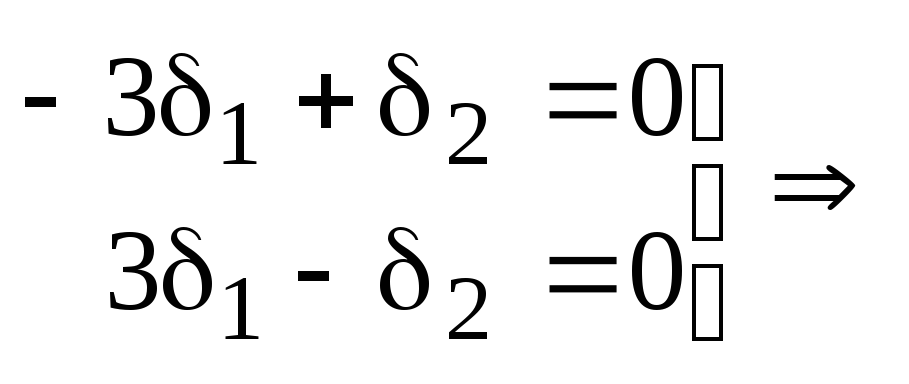
![]() .
.
Пусть
![]() ,
тогда
,
тогда![]() и
и
![]() .
.
Общим решением исходной системы будет вектор функция:
![]() или в координатной форме:
или в координатной форме:
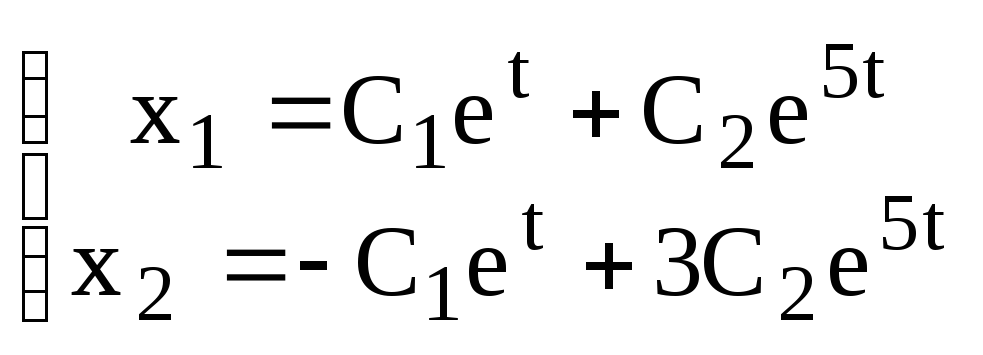
б) С помощью операционного исчисления найти общее решение системы:
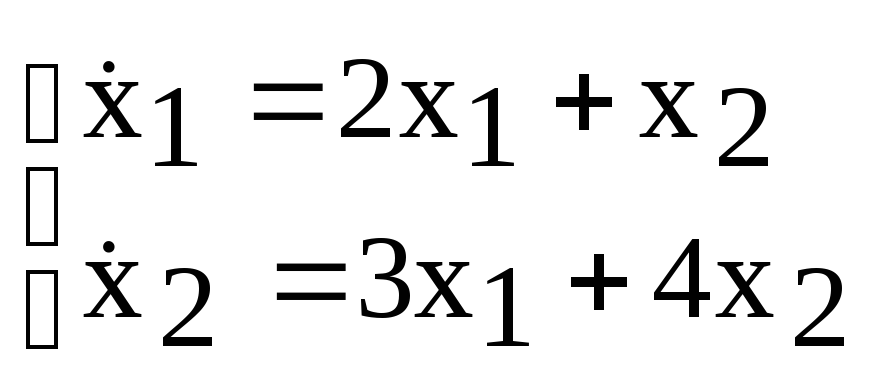
Применим преобразование Лапласа к обеим частям каждого уравнения:
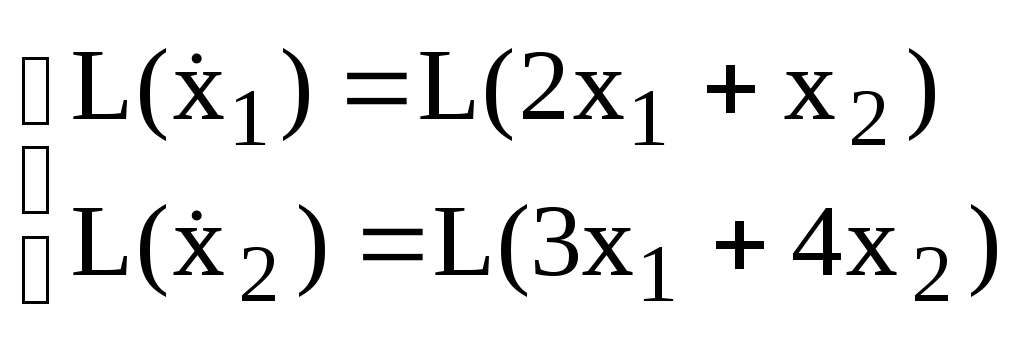
Пользуясь свойством линейности преобразования и теоремой о дифференцировании оригинала:
![]()
получим:
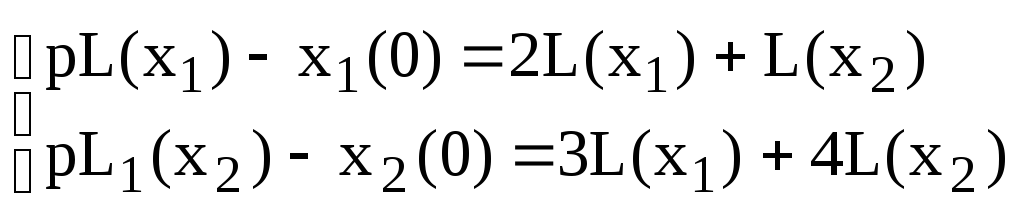
Т. к.
![]() и
и![]() не
заданы, то считаем их произвольными
величинами:
не
заданы, то считаем их произвольными
величинами:
![]()
Тогда
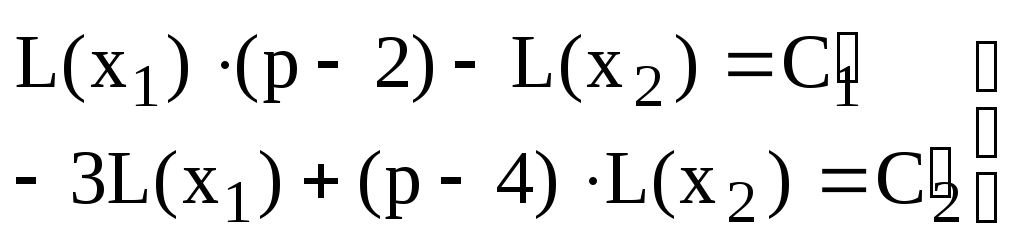
Откуда
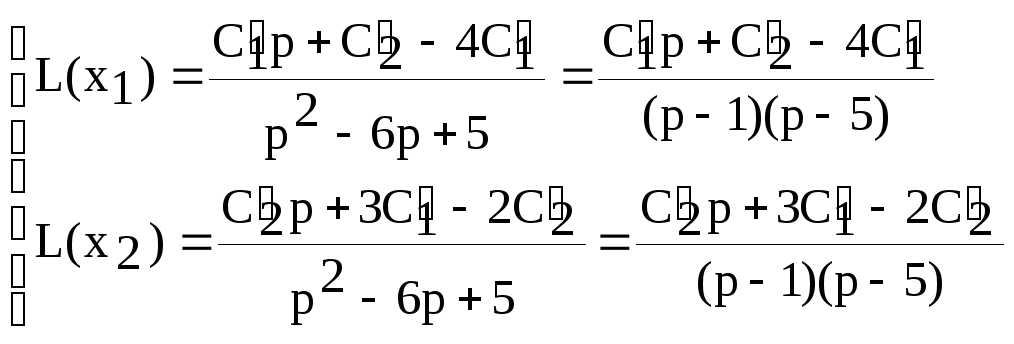
Для восстановления оригиналов
![]() и
и![]() разложим дроби на простейшие:
разложим дроби на простейшие:
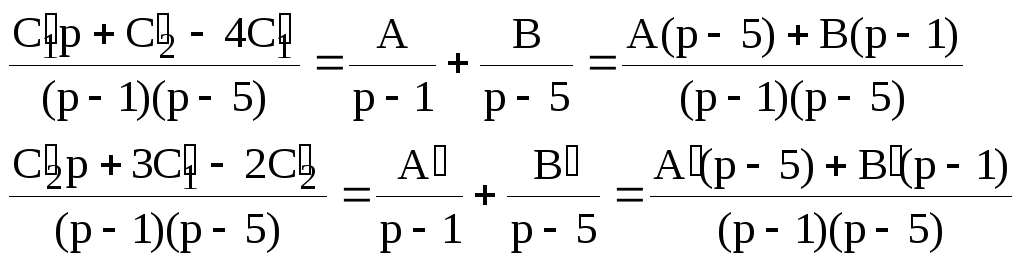
Тогда
![]()
Поскольку
![]() и
и![]() —
произвольные, то можно ввести обозначения:
—
произвольные, то можно ввести обозначения:
![]()
Поэтому:![]()
Так как для изображения
![]() оригиналом является
оригиналом является![]() ,
то получаем общее решение системы:
,
то получаем общее решение системы:
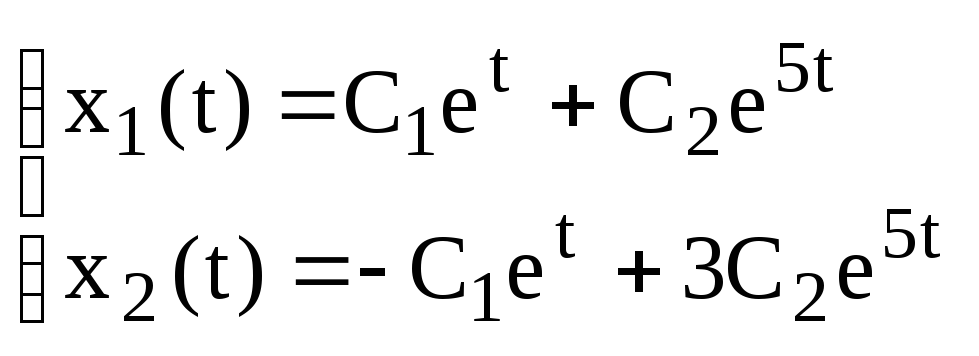
![]()
Решение типового варианта контрольной работы n6.
Задание 6.1. Исследовать сходимость
числового ряда![]() .
.
Решение: Воспользуемся признаком Д'Аламбера:
![]() ,
,![]()
![]() Следовательно,
ряд сходится.
Следовательно,
ряд сходится.
Задание 6.2. Исследовать сходимость
числового ряда![]() .
.
Решение. Применим радикальный
признак Коши:
![]() ,
,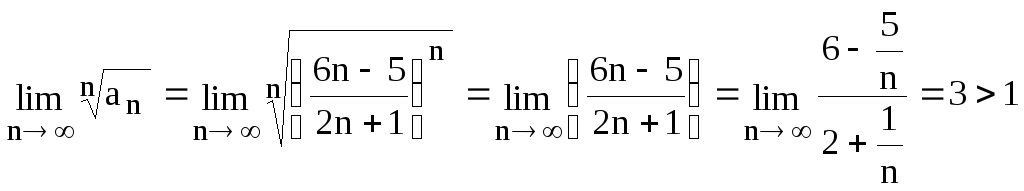 ,т.о. ряд расходится.
,т.о. ряд расходится.
Задание 6.3. Исследовать сходимость
числового ряда
![]() .
.
Решение. Применим интегральный
признак Коши. Функция![]()
удовлетворяет условиям признака.
Исследуем несобственный интеграл
![]() .
Т.к. интеграл сходится, то сходится и
данный ряд.
.
Т.к. интеграл сходится, то сходится и
данный ряд.
Задание 6.4. Исследовать сходимость числового ряда
![]() .
.
Решение. Воспользуемся предельным признаком сравнения.
Сравним данный ряд и ряд
![]() ,
который расходится.
,
который расходится.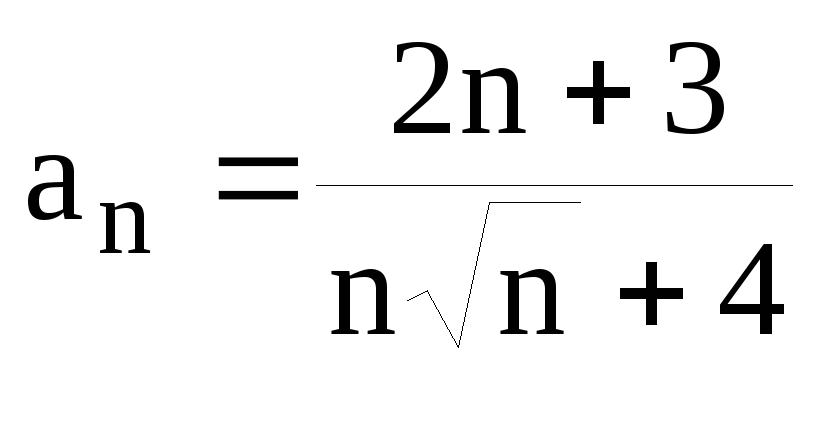 ,
,![]() .
.
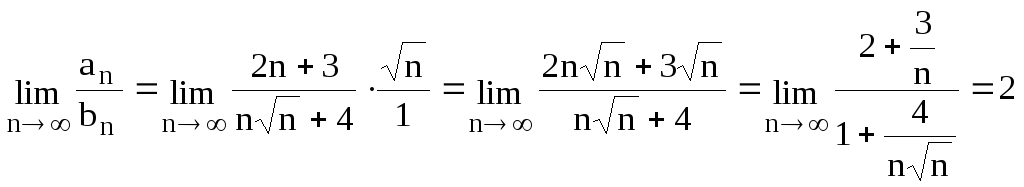 .
Значит, исследуемый ряд расходится, так
же как и ряд
.
Значит, исследуемый ряд расходится, так
же как и ряд![]() .
.
Задание 6.5. Исследовать сходимость
числового ряда
![]() .
.
Решение. 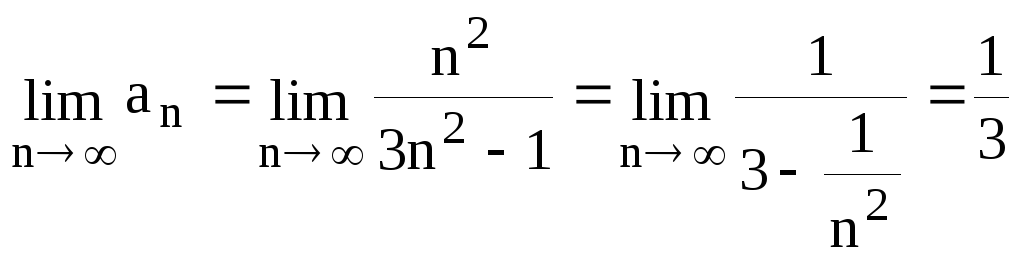 .
Ряд расходится, т.к.
.
Ряд расходится, т.к.
не выполняется необходимый признак
сходимости рядов
![]() .
.
Задание 6.6. Исследовать на сходимость,
абсолютную и условную знакочередующийся
ряд
![]() .
.
Решение.Данный знакочередующийся ряд сходится по признаку Лейбница,
т.к.
![]() и
и![]() .
Этот ряд сходится абсолютно, т.к. ряд из
абсолютных величин его членов
.
Этот ряд сходится абсолютно, т.к. ряд из
абсолютных величин его членов![]() сходится по признаку Коши, т.к.
сходится по признаку Коши, т.к.
![]() .
.
Задание 6.7. Исследовать на сходимость,
условную или абсолютную сходимость
знакочередующийся ряд
![]() .
.
Решение. Представим данный ряд в
виде суммы двух рядов![]() .
Для ряда
.
Для ряда![]() выполняется
выполняется
признак Лейбница
![]() и
и![]() ,
т.е. ряд сходится. Т.к. ряд
,
т.е. ряд сходится. Т.к. ряд![]() ,
составленный из абсолютных величин
ряда
,
составленный из абсолютных величин
ряда![]() ,
есть гармонический ряд (расходящийся),
то ряд
,
есть гармонический ряд (расходящийся),
то ряд![]() сходится условно. Исходный ряд
сходится условно. Исходный ряд![]() как сумма сходящегося условно ряда
как сумма сходящегося условно ряда![]() и
расходящегося ряда
и
расходящегося ряда![]() ,
расходится.
,
расходится.
Задание 6.8. Найти область сходимости
степенного ряда
![]() .
.
Решение.Для данного степенного
ряда вида![]() ,
,![]() ,
,![]() .
.
Радиус сходимости
![]() .
Следовательно, ряд сходится в интервале
(-3; 3). Исследуем сходимость ряда на концах
интервала. Положим сначала x = 3.
.
Следовательно, ряд сходится в интервале
(-3; 3). Исследуем сходимость ряда на концах
интервала. Положим сначала x = 3.
Получим числовой ряд
![]() ,
который расходится (сравним с гармоническим
рядом
,
который расходится (сравним с гармоническим
рядом![]() ).
Возьмем теперь x = -3. Получим
знакочередующийся ряд
).
Возьмем теперь x = -3. Получим
знакочередующийся ряд![]() ,
который сходится условно по признаку
Лейбница
,
который сходится условно по признаку
Лейбница
(см. решение примера 6.7.). Таким образом,
область сходимости ряда - полуинтервал
![]() .
.
Задание 6.9. Найти область сходимости
степенного ряда
![]() .
.
Решение.Для данного степенного
ряда вида![]() ,
,![]() ,
,![]() ,
x0 = -2. Определим радиус сходимости
ряда
,
x0 = -2. Определим радиус сходимости
ряда![]() .
Таким образом, ряд сходится в интервале
(x0- R, x0+ R), т.е. (-2-5;-2+5) или
(-7;3). Исследуем сходимость ряда на концах
интервала. Возьмем x=3. Получим числовой
ряд
.
Таким образом, ряд сходится в интервале
(x0- R, x0+ R), т.е. (-2-5;-2+5) или
(-7;3). Исследуем сходимость ряда на концах
интервала. Возьмем x=3. Получим числовой
ряд![]() .
.
Предел общего члена этого ряда
![]() ,
следовательно, ряд расходится. При x =
-7 получим знакочередующийся ряд
,
следовательно, ряд расходится. При x =
-7 получим знакочередующийся ряд![]() ,
для которого не выполняется признак
сходимости Лейбница
,
для которого не выполняется признак
сходимости Лейбница![]() .
Значит, и при x = -7 данный степенной ряд
расходится. Таким образом, исходный
степенной ряд сходится в интервале
.
Значит, и при x = -7 данный степенной ряд
расходится. Таким образом, исходный
степенной ряд сходится в интервале![]() .
.
Замечание. Область сходимости степенного
ряда можно находить и как для произвольного
функционального ряда
![]() .
В этом примере
.
В этом примере![]() .
По признаку Д'аламбера
.
По признаку Д'аламбера
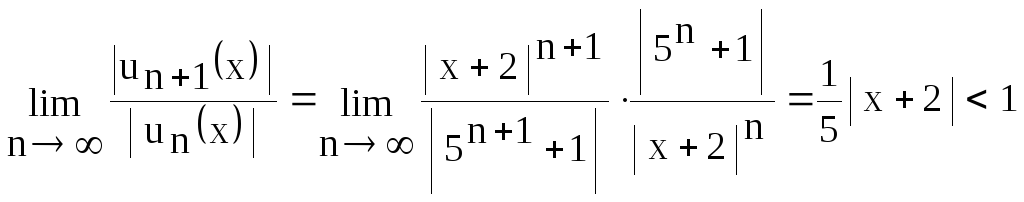 .
Отсюда
.
Отсюда![]() .
Далее, как и выше, последует сходимость
в точках
.
Далее, как и выше, последует сходимость
в точках![]() и
и![]() .
.
Задание 6.10.Разложить в ряд Тейлора
функцию![]() в окрестности точки
в окрестности точки![]() .
Найти область сходимости полученного
ряда.
.
Найти область сходимости полученного
ряда.
Решение. Искомое разложение можно найти
с помощью формулы
![]()
![]()
![]() ,
,
положив в ней
![]() и вычислив значения производных функции
и вычислив значения производных функции![]() при
при![]() .
Но проще получить разложение, используя
известное разложение для функции
.
Но проще получить разложение, используя
известное разложение для функции
![]() ,
,
в котором ряд справа сходится к функции
![]() в интервале (-1,1).
в интервале (-1,1).
Представим
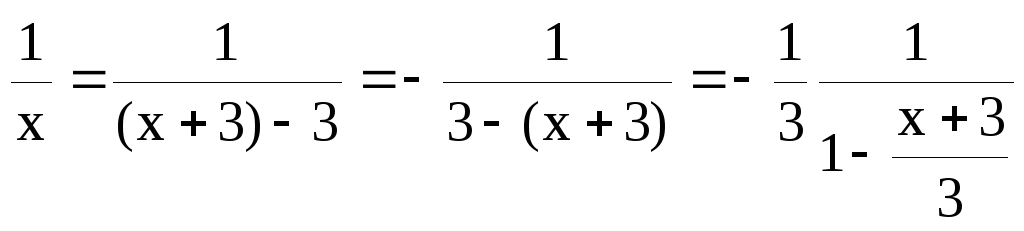 .
Применяя указанное разложение, получим
.
Применяя указанное разложение, получим
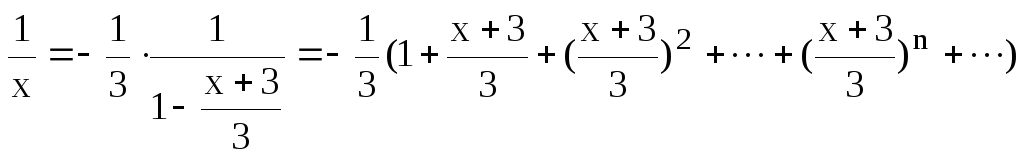 .
.
Так как, ряд, который использовали для
разложения, сходится для
![]() ,
то данный ряд сходится для
,
то данный ряд сходится для![]() ,
отсюда
,
отсюда![]()
![]() .
Таким образом, полученный степенной
ряд является рядом Тейлора функции
.
Таким образом, полученный степенной
ряд является рядом Тейлора функции![]() в окрестности точки
в окрестности точки![]() и
его областью сходимости является
интервал (-6,0).
и
его областью сходимости является
интервал (-6,0).
Задание 6.11.Используя разложение
подынтегральной функции в степенной
ряд, вычислить определенный интеграл![]() с точностью до 0.001.
с точностью до 0.001.
Решение. Воспользуемся рядом Маклорена
для
![]() ,
тогда
,
тогда![]() .
.
Почленно интегрируя этот ряд в промежутке [0;0.5], получим
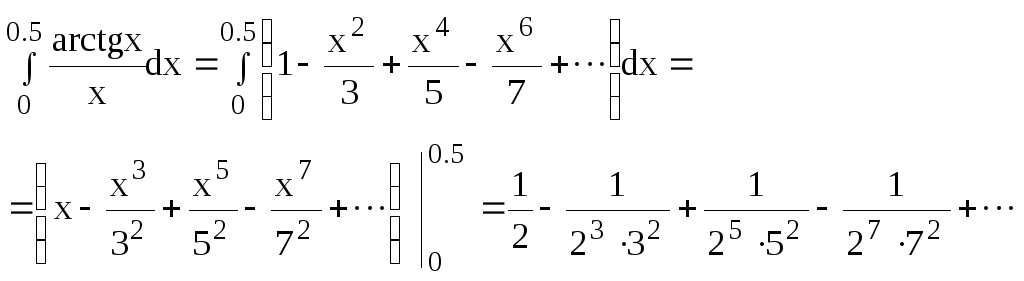
Полученный числовой ряд есть ряд
Лейбница. Погрешность, происходящая от
отбрасывания всех членов ряда, начиная
с четвертого
![]() ,
поэтому, чтобы достичь требуемой точности
достаточно взять три первых слагаемых
,
поэтому, чтобы достичь требуемой точности
достаточно взять три первых слагаемых![]()
Задание 6.12.Разложить в ряд Фурье
периодическую с периодом![]() функцию
функцию
![]() =
=![]()
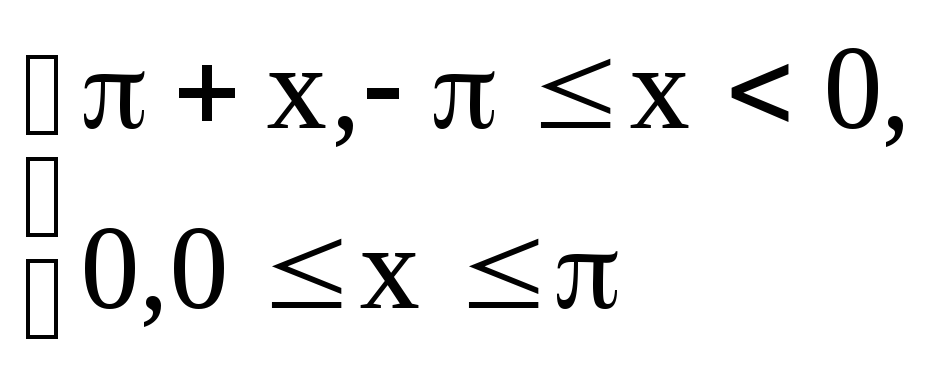
Решение. Вычислим коэффициенты Фурье:
![]()
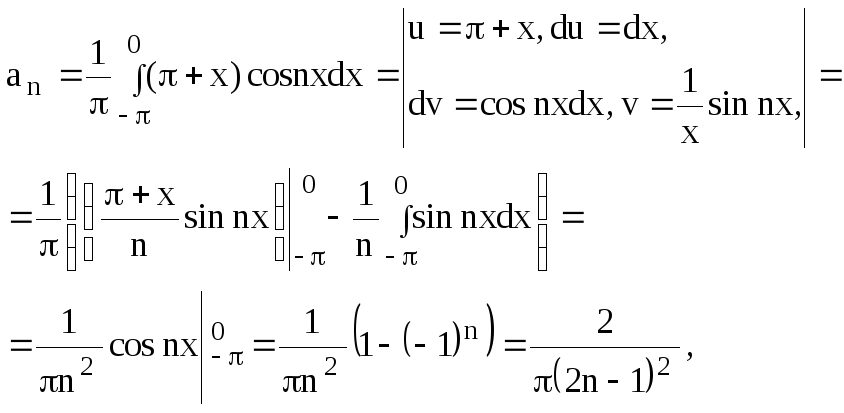

Ряд Фурье для данной функции запишется в виде
![]()
Задание 6.13.Разложить в ряд Фурье
функцию![]() заданную в интервале (0;
заданную в интервале (0;![]() ),
продолжив (доопределив) ее четным и
нечетным образом. Построить графики
для каждого продолжения.
),
продолжив (доопределив) ее четным и
нечетным образом. Построить графики
для каждого продолжения.
Решение. Продолжим данную функцию четным образом. Тогда:
![]()
![]()
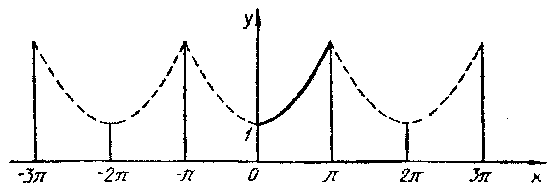
Найдем неопределенный интеграл
![]() выполнив дважды интегрирование по
частям:
выполнив дважды интегрирование по
частям:
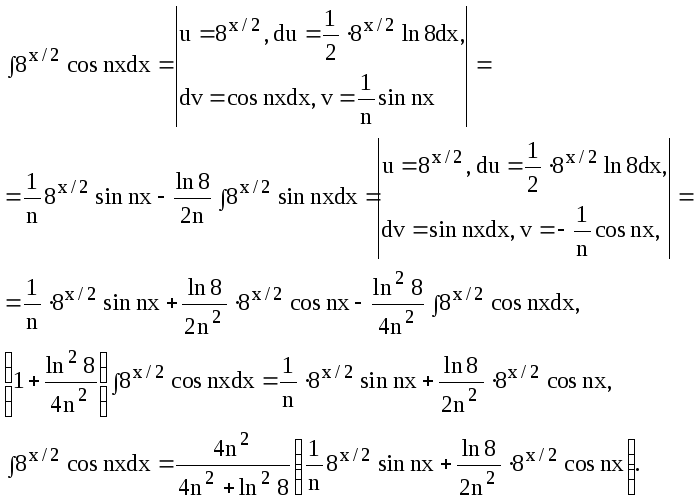
Вычислим коэффициенты
![]() :
:
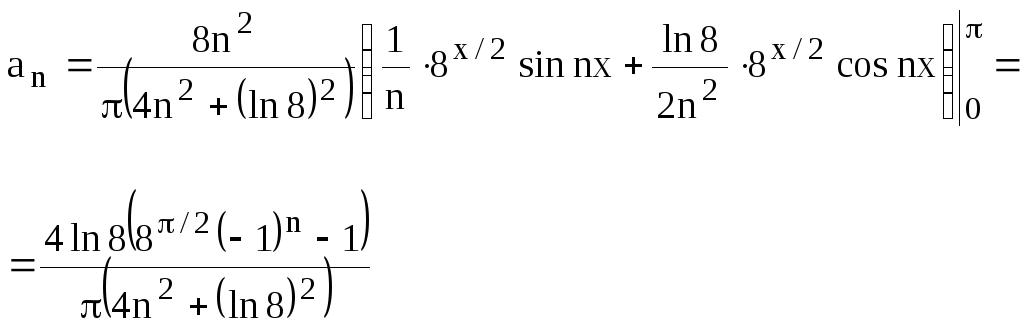
Следовательно, разложение данной функции по косинусам имеет вид:
![]()
Теперь продолжим данную функцию нечетным образом. Тогда:
![]()

![]()
Следовательно, разложение данной функции по синусам имеет вид:
![]()
Задание 6.14.Разложить в ряд Фурье
периодическую (с периодом![]() )
функцию
)
функцию
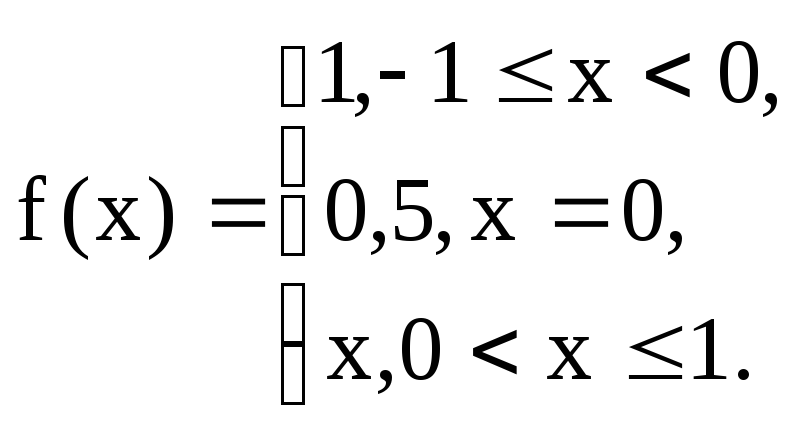
Решение. Вычисляем коэффициенты
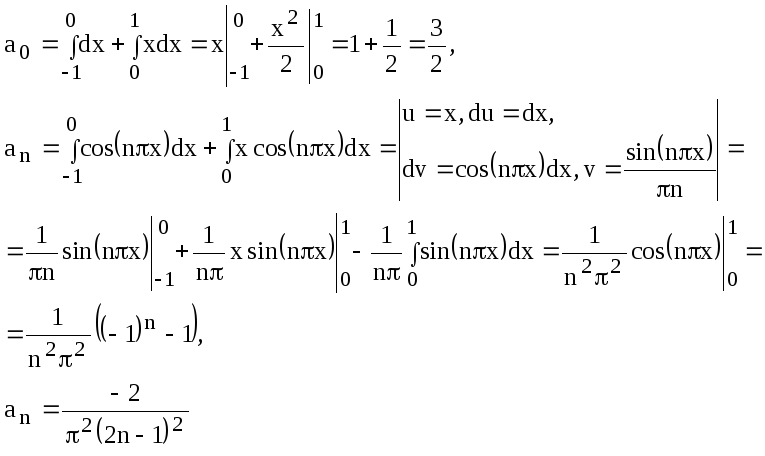
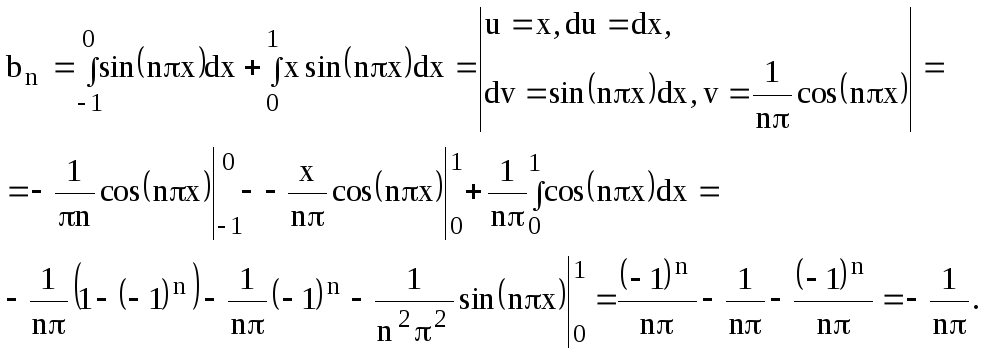
В итоге получаем следующий ряд Фурье:
![]()
Задание 6.15.Разложить в ряд Фурье по косинусам функцию
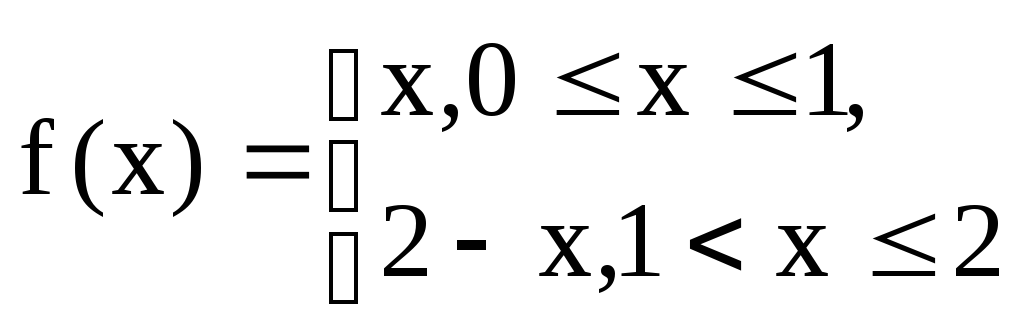
на отрезке [0;2] и найти сумму ряда
![]()
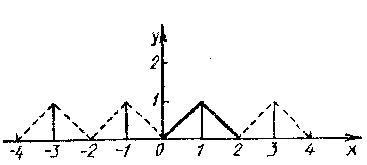
Решение. Продолжим функцию четным образом и вычислим коэффициенты Фурье:
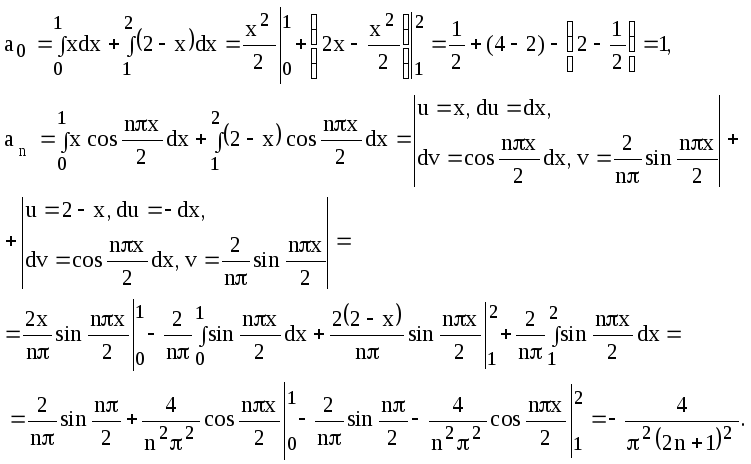
Следовательно,
![]()
Полагая
![]() получаем:
получаем:
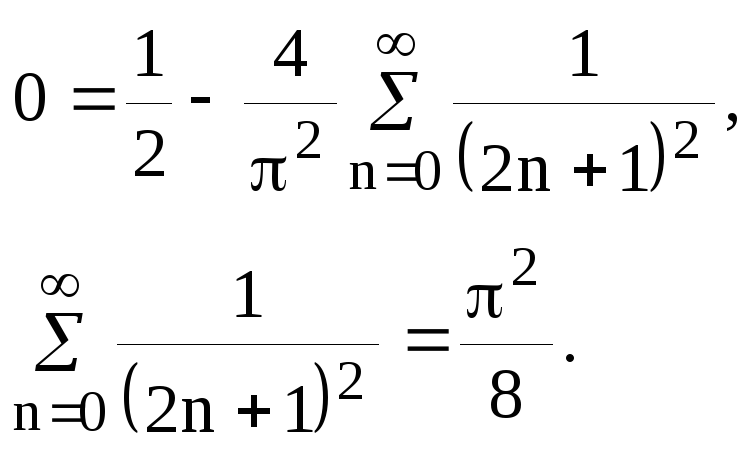
Таким образом, с помощью ряда Фурье мы нашли сумму числового ряда.
