Решение типового варианта

контрольной работы №5

Задание 5.1. Найти общее решение:

.

Преобразуем данное уравнение:

.

Это уравнение с разделяющимися переменными. Разделим переменные

Интегрируем обе части неравенства:

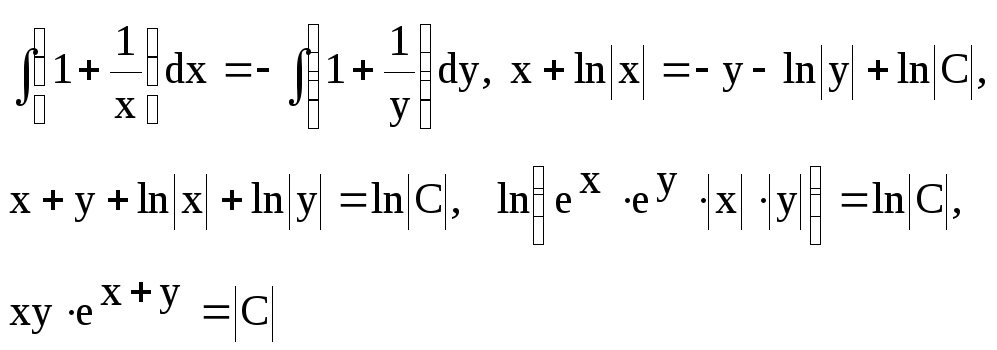
Последнее равенство является общим интегралом исходного уравнения.

Задание 5.2. Найти общее решение:

.

Так как функциии— однородные второго измерения

то данное уравнение — однородное.

Сделаем замену: где— новая неизвестная функция.

.

Тогда:

,.

Далее имеем:

,.

Это уравнение с разделяющимися переменными. Решаем его:

.

В последнее выражение вместо подставим значение.

Получим общий интеграл:

Выразив отсюда , найдём общее решение исходного уравнения :

.

Задание 5.3. Найти общее решение:

.

Это линейное неоднородное уравнение. Рассмотрим однородное:

.

Решим его:

,,

По методу Лагранжа общее решение линейного неоднородного уравнения ищем в виде ,где— неизвестная функция.

Подставим это выражение в исходное уравнение:

.

Получим простейшее дифференциальное уравнение 1-ого порядка:

,,.

Окончательно, общее решение нашего уравнения имеет вид :

.

Задание 5.4. Найти общее решение:

Введём обозначения:

Так как;, а следовательно, то уравнение является уравнением в полных дифференциалах, а его левая часть есть полный дифференциал, причем

Далее:

;

т.е.

,, а,.

Общий интеграл исходного уравнения имеет вид U (x, y)=C или

.

Задание 5.5. Найти общее решение:

Это уравнение 2-ого порядка, не содержащее искомой функции . Оно допускает понижение порядка уравнения заменой,.

После замены исходное уравнение превращается в однородное уравнение первого порядка:

.

Делаем подстановку:

,.

Тогда

.

Разделяем переменные:

,,;

..

Так как , то

Находим:

.

Общее решение уравнения имеет вид:

.

Задание 5.6. Найти общее решение:

Это уравнение второго порядка, не содержащее независимой переменной . Оно допускает понижение порядка уравнения заменой:

,

После замены, исходное уравнение преобразуется в уравнение с разделяющимися переменными:

Решаем это уравнение:

,

Так как , то.

Снова получили уравнение с разделяющимися переменными, поэтому

,.

Значит, — общее решение нашего уравнения.

Задание 5.7. Решить задачу Коши:

,,,

Составляем характеристическое уравнение и решаем его:

,,,,.

Общее решение исходного уравнения имеет вид:

.

Находим:

.

Используем начальные условия

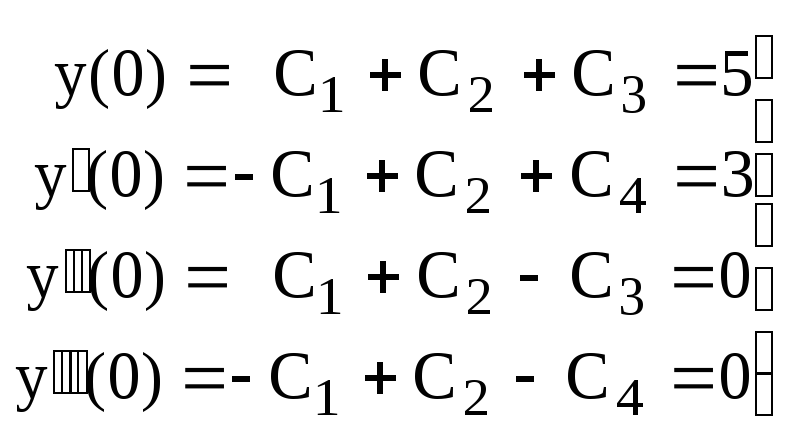
Решаем систему:

,,,.

Решение задачи Коши имеет вид:

.

Задание 5.8. Найти общее решение:

.

Находим корни характеристического уравнения:

Следовательно общее решение однородного уравнения имеет вид

(;— фундаментальная система решений):

.

Правая часть уравнения представляет собой сумму функций и.

Для нахождения частных решений, соответствующих этим функциям составляем:

для

S=1 (кратность числасреди корней характеристического уравнения)

;

для :

(кратность числасреди корней характеристического уравнения).

т.е. — частное решение нелинейного уравнения с неизвестными коэффициентами.

Подставляем в исходное уравнение:

Для выполнения тождества необходимо равенство коэффициентов:

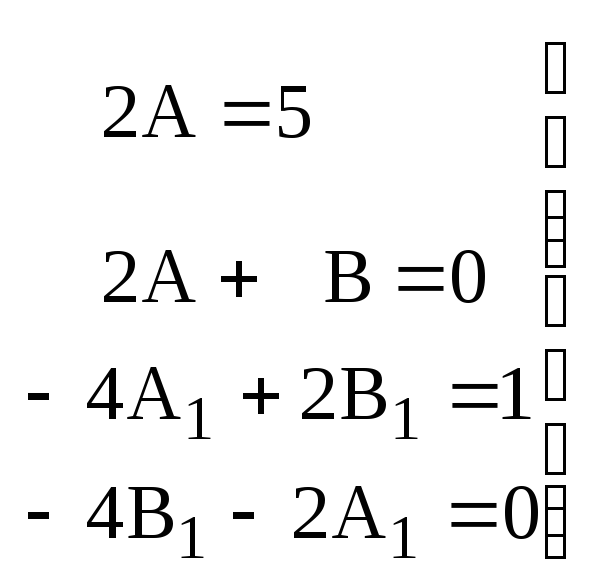
Поэтому:

Таким образом, частное решение исходного уравнения имеет вид:

,

а его общее решение: