
Математический_анализ_2_семестр
.pdf
Классификация точек покоя для автономных систем второго и третьего порядков.
Система второго порядка.
Запишем уравнение автономной системы второго порядка |
|
|
x |
Ax |
|
|
|
|
x a11 x a12 y |
|
x |
0 |
||||
|
|
|
|
|
|
|
. |
|
|
. Точка покоя |
|
||||
a21 x a22 y |
|
|
|
|
0 |
|
|
y |
|
y |
|
|
|||
1. |
Корни характеристического уравнения 1 , 2 действительны.. |
|||
x |
|
C |
|
|
|
|
C e 1t 1 |
e 2t 2 |
|
|
|
1 |
2 |
|
y |
|
|
|
|
а) 1 0, 2 0 .
При t x t 0, y t 0. Поэтому точка покоя (или тривиальное решение) асимптотически устойчива.
Заметим, что первое слагаемое – это проекция траектории на ось 1 ,
второе слагаемое – проекция на ось 2 .
2
Такая точка покоя называется
устойчивый узел.
|
|
|
|
|
|
|
1 |
б) 1 0, 2 0 . |
|
|
|
Этот случай можно рассматривать |
как |
предыдущий, |
|
если формально положить t < 0. Получим те же траектории, что и в п. а), но стрелки на них будут направлены в другую сторону. Направление движение другое (t<0). Такая точка называется неустойчивый узел.
в) 1 0, 2 0 .
По вектору 1 мы, находясь на траектории, стремимся к нулю, по вектору
2 , наоборот, удаляемся от нуля.
Такая точка покоя - седло.
г) 1 0, 2 0 .
Это – тоже седло, но стрелки направлены в другую сторону.
Траектория прижимается к той оси, для которой модуль характеристического числа меньше.
Седла – неустойчивые точки покоя.
Заметим, в ситуациях узлов и седла траектория, начавшись в определенном квадранте, в нем и остается.
91

д) 1 2 .
Точка покоя – дикритический узел,
Устойчивый при 0, неустойчивый при 0
е) 1 0, |
2 0 |
|
|
|
|
|
|
|
||
Точка покоя - вырожденный узел, |
при |
1 0 |
устойчивая, но |
|||||||
не асимптотически устойчивая. |
Если |
|
1 0 , то точка покоя |
- неустойчивая |
||||||
(стрелки направлены в обратную сторону) |
|
|
|
|||||||
ж) |
|
1 0, 2 0 . |
Точка |
безразличного равновесия. При изменении |
||||||
|
|
|
x t |
|
|
|
остается на месте. |
Этими точками |
||
времени любая точка |
C 1 C 2 |
|||||||||
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
y t |
|
|
|
|
|
|
|
заполнена вся плоскость. |
|
|
|
|
|
|
|
|||
2. Корни характеристического уравнения комплексно сопряженные. |
||||||||||
1,2 |
i |
|
|
|
|
|
|
|
||
x |
|
|
|
|
|
|
|
|
|
|
|
|
e t C u cos t |
v sin t C |
2 |
u sin t v cos t |
|
||||
|
|
|
1 |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
Параметр t имеет смысл угла поворота вокруг начала координат (в периодической составляющей).
а) Если 0 , то траектория приближается к началу координат с ростом t
(спираль), так как e t - убывающая функция. Точка покоя устойчивый фокус асимптотически устойчива
б) если 0 , то траектория удаляется от начала координат с ростом t
(спираль), так как e t - возрастающая функция. Точка покоя неустойчивый фокус неустойчива
в) если 0 , то траектории представляют собой эллипсы, охватывающие начало координат. Точка покоя центр устойчива, но не асимптотически
устойчива. |
|
|
а) |
б) |
в) |
x x y
Пример. ,
y x y
1 |
|
, |
|
A |
|
|
|
|
1 |
|
|
1 |
|
|
|
Классифицировать точки покоя в зависимости от параметра.
92

|
A E |
|
2 2 1 , |
|
|
|
|||||
|
|
1 |
|||||||||
|
|
||||||||||
|
|
|
|
|
|
|
|
1,2 |
|
|
|
1) |
0 |
|
|
|
|
|
|
|
|||
а) |
1, |
1 0, 2 |
0 седло, |
|
|
|
|||||
б) |
1, |
1 |
0, 2 |
0 |
неустойчивый узел |
||||||
в) |
1, |
1 |
2, 2 |
0 |
вырожденный узел |
||||||
2) |
0 |
1,2 - комплексно сопряженные. |
|||||||||
Так как Re 1 Re 2 1 0 , то точка покоя – неустойчивый фокус 3) 0 1 2 1, точка покоя – неустойчивый дикритический узел.
Система третьего порядка.
Запишем уравнение автономной системы третьего порядка |
|
|
x |
Ax |
|
|
|
|
x |
|
a |
|
|
|
|
11 |
y |
|
a21 |
|
|
|
|
|
z |
|
a31 |
|
a |
a |
x |
|
12 |
13 |
|
|
a22 |
a23 |
y . |
|
a32 |
a33 |
|
|
z |
|||
1) Все корни характеристического уравнения действительны и различны.
x |
|
|
|
|
|
|
|||
y |
C1e 1t 1 |
C2 e 2t 2 |
C3e 3t 3 . |
|
|
|
|
|
|
z |
|
|
|
|
Картину поведения фазовых траекторий довольно легко представить, рассматривая поведение фазовых траекторий в плоскостях, натянутых на пары собственных векторов. Этот случай уже изучен выше.
а) 1 0, 2 0, 3 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
В плоскостях 1 , 2 , |
|
1 , 3 , |
2 , 3 , имеем устойчивые узлы. Такая |
||||||||||||||||
точка покоя так и называется – устойчивый узел. |
, |
|
|
|
, |
|
|
|
, имеем |
||||||||||
б) |
0, |
|
0, |
|
0 |
В плоскостях |
|
|
|
|
|||||||||
2 |
3 |
1 |
, 2 |
|
1 |
, 3 |
|
2 |
, 3 |
||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
неустойчивые узлы. Такая точка покоя называется – неустойчивый узел.
3
2
1
а) |
б) |
93
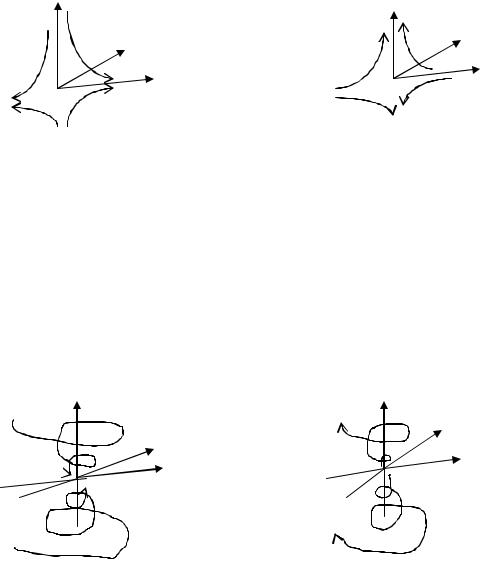
в) один корень имеет знак, противоположный остальным двум корням. Точка покоя в этом случае называется седло – узел и является неустойчивой точкой покоя.
|
Пусть, например, |
0, |
|
0, |
|
0 |
. Тогда в плоскости |
|
|
имеем |
||||||||||
|
2 |
3 |
|
1 , 2 |
||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
3 , |
|
|
|
|
|
||
неустойчивый |
|
узел, |
а |
в |
плоскостях |
|
- |
седла. |
Если |
|||||||||||
|
|
1 |
, |
|
2 , 3 |
|||||||||||||||
|
0, |
|
0, |
|
0 , |
то в плоскости |
|
|
|
|
имеем |
устойчивый узел, а в |
||||||||
2 |
3 |
|
1 |
, 2 |
||||||||||||||||
1 |
|
|
|
|
|
- седла. |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
плоскостях 1 , 3 , |
2 , |
3 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
1 0, 2 0, 3 0 . |
|
|
|
|
|
|
1 0, 2 0, 3 0 |
|
|||||||||||
Заметим, что в ситуациях узлов и седла – узел траектория, начавшись в определенном октанте, не переходит в другой октант.
|
2) |
3 - действительный |
корень характеристического уравнения, |
|
1,2 |
i - комплексно сопряженная пара корней. |
|||
|
Заметим, что при изменении номера корней ситуация будет аналогичной. |
|||
|
|
|
|
|
|
В плоскости |
1 , 2 имеем фокус, устойчивый при 0 , неустойчивый |
||
при 0 . |
|
|
|
|
|
а) 3 |
0 0 . Такая точка покоя называется устойчивый фокус. |
||
|
б) 3 |
0 0 . Такая точка покоя называется неустойчивый фокус. |
||
|
|
3 0 0 |
3 0 0 |
|
|
в) |
3 0 0 или 3 0 0 . Такая особая точка называется седло – |
фокус и является неустойчивой. |
||
|
|
|
|
В первом случае по оси 3 точка по траектории приближается к плоскости |
|
|
и уходит от начала координат, так как на самой плоскости имеем |
|
1 |
, 2 |
|
неустойчивый фокус.
94
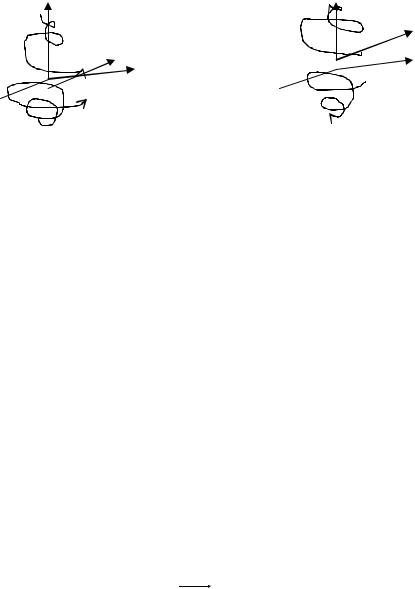
|
|
|
имеем устойчивый фокус, |
Во втором случае на плоскости |
1 |
, 2 |
поэтому траектория стремится к оси 3 , но удаляется от начала координат по этой оси, так как 3 0 .
3 0 0 |
3 0 0 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Функция Ляпунова, «вторая метода Ляпунова».
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||
|
|
Рассмотрим автономную систему x |
f |
x |
, x |
|
... и |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
функцию V x1 ,... xn . |
|
|
|
|
|
|
|
|
xn |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Назовем эту функцию знакоположительной, если V x1 ,... xn 0 , |
|
|
|
|||||||||||||||||
|
|
знакоотрицательной, если V x1 ,... xn 0 |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Назовем функцию V x1 ,... xn положительно определенной, если |
|
|
|
|||||||||||||||||
|
|
1) |
она знакоположительна, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
2) |
V x1 ,... xn 0 x1 |
0,... xn |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Назовем функцию V x1 ,... xn отрицательно определенной, если |
|
|
|
|||||||||||||||||
|
|
1) |
она знакоотрицательна, |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
2) |
V x1 ,... xn 0 x1 |
0,... xn |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
Назовем функцию |
V |
x1 ,... xn |
знакоопределенной, если она является |
|||||||||||||||||
отрицательно определенной или положительно определенной. |
|
|
|
|||||||||||||||||||
|
|
Введем |
производную |
функции |
V x1 ,... xn |
в |
силу |
системы |
|
|
|
|||||||||||
|
|
x |
f |
x : |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dV |
n |
V |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f k . Заметим, |
что |
dV |
gradV , f . Поэтому, |
если |
dV |
0 , |
то угол |
||||||||||||
|
dt |
k 1 |
xk |
|
|
|
dt |
|
|
|
|
|
|
|
|
dt |
|
|
|
|||
между градиентом V и вектором правых частей системы тупой. Следовательно, убывание функции V соответствует движению по фазовым траекториям внутрь линии уровня V x1 ,... xn =С.
На этом основан метод функций Ляпунова. Этот метод сводится к трем теоремам Ляпунова.
Теорема Ляпунова об устойчивости. Пусть существует функция
V x1 ,... xn (функция Ляпунова), положительно определенная и имеющая
знакоотрицательную |
dV |
в некоторой окрестности точки |
|
0 . |
|
|
x |
||||
dt |
|||||
|
|
|
|
95

Тогда тривиальное решение автономной системы |
|
t 0 |
устойчиво по |
x |
Ляпунову.
Теорема Ляпунова об асимптотической устойчивости. Пусть |
||||||||||
существует функция |
V x1 ,... xn |
, положительно определенная |
и |
имеющая |
||||||
|
|
dV |
|
|
|
0 . |
|
|
||
отрицательно определенную |
|
в некоторой окрестности точки x |
|
|
||||||
dt |
|
|
||||||||
|
|
|
|
t 0 асимптотически |
||||||
Тогда тривиальное решение автономной системы |
||||||||||
x |
||||||||||
устойчиво по Ляпунову. |
|
|
|
|
|
|
|
|
||
Теорема Ляпунова о неустойчивости. Пусть |
|
V 0 0 . |
Пусть |
dV |
||||||
|
|
|
||||||||
|
dt |
|||||||||
|
|
|
|
|
|
|
||||
знакоопределена в |
некоторой |
окрестности точки |
0 . Если |
в любой |
||||||
x |
||||||||||
|
0 найдутся такие точки, в которых знаки |
V x1 ,... xn и |
||||||||
окрестности точки x |
||||||||||
dVdt совпадают, то тривиальное решение автономной системы неустойчиво.
Пример. |
x |
x y x3 y 2 |
|
|
|
|
|
|
|||||||
|
|
y x y xy |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Выберем V x 2 y 2 |
|
|
|
|
|
|
|||||||||
|
dV |
|
V f |
|
V f |
|
2x x y x3 y 2 2 y x y xy |
2x 2 |
1 x 2 2 y 2 |
||||||
|
|
|
1 |
2 |
|||||||||||
|
dt |
x |
|
y |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
V положительно |
определена, |
dV |
отрицательно определена. |
Поэтому |
|||||||||||
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
тривиальное решение асимптотически устойчиво. |
|
|
|
|
|||||||||||
Пример. |
x y x3 |
|
|
|
|
|
|
||||||||
|
|
x y 3 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
y |
|
|
|
|
|
|
||||
Выберем V x 2 y 2 |
|
|
|
|
|
|
|||||||||
|
dV |
|
V f |
|
V f |
|
2x y x3 2 y x y3 |
2 x 4 |
y 4 |
|
|
||||
|
|
1 |
2 |
|
|
||||||||||
|
dt |
x |
|
y |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
dV
V и положительно определены, поэтому тривиальное решение dt
неустойчиво.
Лекция 25. Приближенное вычисление интеграла.
b
Часто нужно вычислить интеграл f x dx , а аналитически это сделать
a
невозможно (интеграл не берется) или слишком громоздко. Тогда применяют приближенные методы вычисления интеграла на отрезке, по которым пишут алгоритмы и программы реализации этих методов на ЭВМ. Численный расчет дает значение интеграла с некоторой погрешностью, которая зависит как от погрешности метода, так и от погрешности вычислений. Чаще всего
96
рассматривают равномерную сетку, разбивая отрезок a, b |
на отрезки длины |
||||||||||||||||
шагом h: x |
|
x |
|
kh, |
k 0, 1,...,n, a x |
|
, b x |
|
, n |
b a |
. |
|
|
|
|||
n |
0 |
0 |
n |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1. |
Формулы прямоугольников. |
|
|
|
|
|
|
|
|
|
|
||||||
Обозначим yk |
f xk . Заменим интеграл интегральной суммой, вычисляя |
||||||||||||||||
площадь под графиком функции как сумму площадей прямоугольников с |
|||||||||||||||||
основанием h, высотами yk . |
|
|
|
|
|
|
|
|
|
|
|||||||
Если на первом отрезке высоту прямоугольника можно выбрать как y0 , |
|||||||||||||||||
тогда на последнем отрезке высота прямоугольника |
yn 1 . |
Получим первую |
|||||||||||||||
формулу прямоугольников |
|
|
|
|
|
|
|
|
|
|
|||||||
b |
x dx h y0 |
... yn 1 . |
|
|
|
|
|
|
|
|
|
|
|||||
f |
|
|
|
|
|
|
|
|
|
|
|||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если на первом отрезке высоту прямоугольника можно выбрать как y1 , |
|||||||||||||||||
тогда на последнем отрезке высота прямоугольника |
yn . |
Получим вторую |
|||||||||||||||
формулу прямоугольников |
|
|
|
|
|
|
|
|
|
|
|||||||
b |
x dx h y1 |
... yn . |
|
|
|
|
|
|
|
|
|
|
|||||
f |
|
|
|
|
|
|
|
|
|
|
|||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f x в ряд |
Оценим погрешность формул прямоугольников. Разложим |
|||||||||||||||||
Тейлора и оценим остаточный член. |
|
|
|
|
|
|
|
|
|
|
|||||||
Для первой формулы прямоугольников |
|
|
|
|
|
|
|
|
|||||||||
b |
|
|
|
|
n 1 x0 k 1 h |
|
|
|
|
|
|
|
|
|
|
||
f |
x dx |
|
|
|
|
yn 1 Mh |
n |
h y0 |
... yn 1 M b a h, |
||||||||
yk y h dx h y0 ... |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
a |
|
|
|
k 0 |
x0 kh |
|
|
|
|
|
|
|
|
|
|
|
|
где M max a, b |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
f x . |
|
|
|
|
|
|
|
|
|
|
|
||||||
Для второй формулы прямоугольников |
|
|
|
|
|
|
|
|
|||||||||
b |
|
|
|
|
n 1 x0 k 1 h |
|
|
|
|
|
|
|
|
|
|
||
f |
x dx |
|
|
|
|
|
|
|
|
|
n |
h y1 |
... yn M b a h, |
||||
yk 1 y h dx h y1 ... yn Mh |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
a |
|
|
|
k 0 |
x0 kh |
|
|
|
|
|
|
|
|
|
|
|
|
где M max a, b |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
f x . |
|
|
|
|
|
|
|
|
|
|
|
||||||
Таким образом, обе формулы прямоугольников дают погрешность порядка h и являются формулами первого порядка точности.
Можно повысить точность формулы прямоугольников за счет вычисления функции в серединах отрезков разбиения. Получаем третью формулу прямоугольников
b |
|
|
|
|
|
|
|
0 |
|
|
f x dx h f x |
|
|
|
a |
|
|
|
|
h |
|
|
|
h |
|
|
|
|
... f x |
n 1 |
|
|
. |
|
|
|||||
2 |
|
|
|
|
||
|
|
2 |
|
|||
Оценим погрешность этой формулы.
97

|
|
b |
|
|
|
|
|
|
|
|
n 1 x0 k 1 h |
|
|
|
|
|
|
h |
|
|
|
|
|
|
h |
|||||||||||||
|
f x dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
f xk |
|
|
f |
|
|
|
|
|
x xk |
||||||||||||||||||||||||||
|
|
|
|
|
|
xk |
|
|
||||||||||||||||||||||||||||||
|
|
a |
|
|
|
|
|
|
|
|
k 0 |
x0 kh |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
|
||||||||
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
h f x |
0 |
|
|
|
... |
f x |
n 1 |
|
|
|
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h 1 |
|
|
|
|
h x0 |
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|||||||||||||||
f |
|
|
|
|
|
|
|
|
|
k 1 h |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
x xk |
|
|
|
|
|x0 |
kh |
|
|
|
|
|
f |
|
|
|
|
x xk |
||||||||||||
|
xk |
|
|
|
|
|
2 |
|
2 |
|
|
|
|
|
||||||||||||||||||||||||
k 0 |
|
|
|
|
|
|
2 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
M |
2 |
b a h2 |
|||||||||||
|
h f |
x |
|
|
|
|
|
... |
f x |
|
|
|
|
|
|
+0+ |
|
|
|
|||||||||||||||||||
|
0 |
|
|
|
n 1 |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||
|
h |
1 |
|
|
|
h |
2 |
|
|
||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
dx |
|||
|
|
|
|
|
|
||||||||
|
|
|
f x xk |
|
|
|
|||||||
|
2 |
2 |
|
|
|
2 |
|
|
|||||
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
3 |
x0 k 1 h |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
| |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
|
x0 kh |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
Таким |
образом, |
погрешность |
третьей формулы прямоугольников не |
||||||
|
|
M 2 |
|
2 |
|
|
|
|
|
превышает |
|
|
b a h , |
где |
M 2 max a,b f |
|
Эта |
формула |
|
|
|
||||||||
24 |
x . |
||||||||
|
|
|
|
|
|
|
|
||
прямоугольников имеет второй порядок точности.
2. Формула трапеций.
Сложим первую и вторую формулы прямоугольников и разделим пополам. Получим формулу трапеций
b |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
f x |
dx h |
|
|
y0 y1 |
... yn 1 |
|
yn |
|
|
|
|
|
|
||||||||||||||
2 |
|
2 |
|
|
|
|
|
||||||||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Поясним название формулы. Приблизим площадь под графиком функции |
|||||||||||||||||||||||||||
на отрезке kh, k 1 h |
площадью трапеции |
1 |
y |
|
y |
|
. Суммируя площади |
||||||||||||||||||||
|
k |
k 1 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
по всему отрезку интегрирования, получим |
|
|
|
|
|
|
|
|
|||||||||||||||||||
b |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f x |
dx |
y0 |
y1 y1 |
y2 y2 |
... yn 2 |
yn 1 |
yn 1 yn |
||||||||||||||||||||
2 |
|||||||||||||||||||||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
|
y |
... y |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
h |
|
y |
|
n 1 |
|
y |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
2 |
|
|
0 |
1 |
|
|
|
|
|
|
2 |
|
n |
|
|
|
|
|
|
|
|
|
|
|||
Аппроксимируем функцию кусочно – линейной функцией, значения которой совпадают с значениями функции в точках разбиения. Площадь под графиком кусочно – линейной функции на отрезке kh, k 1 h составит
yk h 12 yk 1 yk h 12 yk yk 1 . Суммируя площади по всему отрезку
интегрирования, получим вновь формулу трапеций.
Можно показать, что формула трапеций – формула второго порядка точности. Погрешность вычисления интеграла с помощью этой формулы (это
можно показать) не превышает M122 b a h2 , т.е. в два раза больше, чем по третьей формуле прямоугольников.
3. Формула Симпсона.
98
|
|
|
|
Аппроксимируем |
|
функцию |
f x на |
|
|
отрезке |
|
разбиения квадратичной |
||||||||||||||||||||||||||||||||||||||||
функцией f |
q |
|
ax2 |
|
bx c так, чтобы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
f kh f q |
kh , f |
|
(k 1)h |
f q (k 1)h , |
|
f k 2 h f q k 2 h , k 0, 2,... |
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
v |
ax |
|
|
|
bx c dx |
|
u v |
|
|
|
|
|
|
|
|
|
|
|
u v |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Лемма. |
|
|
|
|
|
|
|
|
|
|
f |
q |
u 4 f |
q |
( |
|
|
|
|
|
) f |
q |
v . |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Докажем лемму для u kh, v (k 2)h . Сделаем замену z x (k 1)h . |
||||||||||||||||||||||||||||||||||||||||||||||||||||
Тогда формула сведется к следующей: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
h |
ax2 bx c dx |
h |
fq h 4 fq 0 fq h . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Левая часть |
|
|
ax2 |
bx c dx |
1 |
ax3 |
|h h |
|
1 |
bx2 |hh |
|
2ch |
2 |
ah3 2ch |
||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Правая часть |
|
|
h |
ah2 bh c 4c ah2 bh c |
|
2 |
ah3 |
|
2ch . Лемма доказана. |
|||||||||||||||||||||||||||||||||||||||||||
|
3 |
3 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
Разобьем теперь отрезок интегрирования |
|
a, b |
|
на 2n частей, ( h |
b a |
). |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x0 , x0 |
|
2h |
|
|
|
|
|
|
|
|
|
|
2n |
|||||||
Применим |
|
|
|
|
лемму |
|
к |
отрезкам |
|
|
, |
|
x0 2h, x0 4h ,..., получим |
|||||||||||||||||||||||||||||||||||||||
формулу Симпсона |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
b |
|
x dx |
h |
y0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 y2n 1 y2n |
||||||||||||||
|
|
|
|
f |
4 y1 |
y2 |
|
y2 4 y3 |
y4 |
...y2n 2 |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
3 |
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
y |
|
4 y 2 y |
|
4 y |
|
2 y |
|
... 2 y |
|
4 y |
|
|
y |
|
. |
|||||||||||||||||||||||||||||||||||
|
|
0 |
2 |
3 |
4 |
2n 2 |
2n 1 |
2n |
||||||||||||||||||||||||||||||||||||||||||||
3 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Можно показать, что формула Симпсона – формула четвертого порядка |
||||||||||||||||||||||||||||||||||||||||||||||||||
точности, |
ее |
погрешность |
|
не |
|
|
|
|
|
превосходит |
|
|
M 4 b a |
h4 , |
где |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
180 |
|
|
|||||||||||||||||||||||||||||||||||||||||||
M4 max a,b f (IV ) x . Это означает, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
что |
|
|
при |
|
|
интегрировании многочлена |
|||||||||||||||||||||||||||||||||||||||||
третьей степени формула Симпсона точна, ее погрешность равна нулю. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|||||
Пример. Вычислить приближенно I = x3 dx |
|
|
|
с шагом h |
. |
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
4 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
I |
1 |
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
27 |
0.14, |
0.11 , |
|
||||||||||||||||||||||
1 формула прямоугольников |
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
64 |
|
|
|
|
8 |
|
|
|
|
|
64 |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
1 |
|
|
|
27 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
2 формула прямоугольников |
I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 0.39, |
0.14 , |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
64 |
|
|
|
|
8 |
|
|
|
64 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
27 |
|
|
|
|
|
|
125 |
|
|
|
|
|
343 |
|
|
|
|
|
|
|
|||||||||||||
3 формула прямоугольников I |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.242 , 0.008 , |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
4 |
|
216 |
216 |
|
|
|
|
|
216 |
|
|
|
|
216 |
|
|
|
|
|
|
|
|||||||||||||||||||||||
Формула трапеций I |
1 |
0.14 0.39 0.265, |
|
|
|
|
0.115. |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
|
|
|
4 |
|
|
|
|
2 |
|
|
|
|
|
4 27 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Формула Симпсона I |
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 0.25, |
0 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
12 |
|
64 |
|
|
|
8 |
|
|
|
|
|
|
|
|
64 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
99
Лекция 26. Обзор численных методов решения задачи Коши для обыкновенных дифференциальных уравнений.
Будем рассматривать схемы численных методов для уравнения первого порядка
y f x, y , y x0 y0 .
Это – самый простой случай, но к нему по аналогии сводятся схемы методов для системы дифференциальных уравнений и для дифференциального уравнения n- го порядка.
1. Методы, основанные на разложении функции в ряд Тейлора.
Запишем разложение функции в ряд Тейлора в окрестности точки x
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
y x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
y x y x x |
y |
|
x |
|
|
|
2! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рассмотрим равномерную сетку по x : a x0 , |
x0 h, x0 2h,... x0 nh,... |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
, x xn 1 , xn 1 xn |
h , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Пусть |
|
x xn |
|
|
тогда |
разложение |
функции |
в |
|
ряд |
|||||||||||||||||||||||||||||||||||||||||
Тейлора можно записать в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
yn 1 |
yn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
... |
yn h xn , |
yn , h , где |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
h y |
xn y |
|
xn |
2 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
xn , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h |
... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
yn , h y |
xn |
y xn |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
Подставим в xn , |
yn , h из дифференциального уравнения |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
y |
xn f xn , yn , |
|
|
y |
xn |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xn , yn |
|
|
' |
|
|
|
' |
xn |
, yn y xn |
, yn |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
f x, y |
|
f x |
xn , yn f y |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
' x |
n |
, y |
n |
f |
|
' x |
n |
, y |
n |
f |
x |
n |
, y |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
x |
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Тогда x |
|
, y |
|
, h x |
|
, |
y |
|
, h |
f |
x |
|
, |
y |
|
|
|
|
h |
( f |
' x |
|
, y |
|
f ' x |
|
, y |
|
f x |
|
, y |
|
) |
||||||||||||||||||
n |
n |
n |
n |
n |
n |
|
|
n |
n |
n |
n |
n |
n |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
x |
|
|
y |
|
|
|
|
|||||||||||||||
yn 1 yn h xn , yn , h . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Это – основная расчетная формула.
Учитывая в xn , yn , h слагаемые с производными высших порядков, получим более точные приближенные формулы.
Если взять xn , yn , h f xn , yn , то получим метод Эйлера yn 1 yn hf xn , yn
2. Методы Рунге – Кутта.
Основная идея методов Рунге – Кутта – вместо вычисления производных высших порядков в xn , yn , h вычислять значения функции в некоторых
точках, отличных от xn .
Выберем
xn , yn , h = c1 f x, y c2 f x ha2 , y hb21 f x, y
Разложим xn , yn , h по h
xn , yn , h = c1 f x, y c2 f x, y + c2 f x' x, y ha2 c2 f y' x, y hb21 f x, y ...=
100
