
КМ - Maple
.pdf
Вычисление произведений членов последовательностей
Для вычисления произведений членов последовательностей используются функции product и mul, разница между которыми аналогична разнице между sum и add.
> Product(k^2, k=1..n) = product(k^2, k=1..n);
n
k2 = Γ(n + 1)2
k=1
Product(k^2-2*k+2, k=1..5) = mul(k^2-2*k+2, k=1..5);
5
(k2 − 2k + 2) = 1700
k=1
Разложение функций в ряды
Для разложения функций в ряд Тейлора используются функции taylor (для функции одной переменной) и mtaylor (для функции нескольких переменных). Для разложения функций одной переменной в обобщенный степенной ряд используется функция series. Для нахождения конкретного коэффициента разложения используют функции coeftayl и coeff, причем последнюю допустимо применять только к уже готовому разложению.
>y := x -> (1+x)/(1-x):
y(x) = taylor(y(x), x=0, 4);
1 + x = 1 + 2x + 2x2 + 2x3 + O(x4) 1 − x
> cot(x) = series(cot(x), x=0, 4);
cot(x) = x−1 − 13x − 451 x3 + O(x4)
> coeff(%, x, 3);
−1 45
>expan := f(x)=taylor(f(x), x=t, 3): subs(t=x[0], expan);
f (x) = f (x0) + D(f )(x0)(x − x0) + 12(D(2))(f )(x0)(x − x0)2 + O((x − x0)3)
> mtaylor(sin(x^2+y^2), [x=0, y=0], 8); x2 + y2 − 16x6 − 12y2x4 − 12y4x2 − 16y6
51

4.5Интегрирование функций
Вычисление простых интегралов
Для вычисления простых интегралов в Maple используется функция int. При вычислении неопределенных интегралов переменная интегрирования задается без диапазона, а в аналитическом представлении результата отсутствует произвольная постоянная.
> f := x -> exp(a*x)*cos(b*x): Int(f(x),x) = simplify(int(f(x),x));
e(ax) cos(bx)dx = e(ax) a cos(bx) + b sin(bx) a2 + b2
>g := x -> x^3*cos(x):
Int(g(x), x=0..2*Pi) = simplify(int(g(x), x=0..2*Pi));
12π2
Функция int позволяет вычислять несобственные интегралы, а также интегралы с переменными пределами интегрирования:
>f := x -> 2/(x^2+4*x+6):
Int(f(x), x=-infinity..infinity) = int(f(x), x=-infinity..infinity);
∞ |
2 |
|
|
|
|
dx = π√2 |
|||
|
||||
x2 + 4x + 6 |
||||
−∞ |
|
|
|
|
>g := x -> sin(x)/x:
Int(g(x), x=-1..1)=int(g(x), x=-1..1);
1
sin(x)
x
= 2 Si (1)
−1
>h := x -> 1/x^2:
Int(h(x), x=0..1) = int(h(x), x=0..1);
1
1
x2 dx = ∞
0
52

> Int(2*x, x=sqrt(x)..x^2) = int(2*x, x=sqrt(x)..x^2);
x2
2x dx = x4 − x2
√x
Интегрирование по частям
С помощью функции intparts из пакета student можно выполнить интегрирование по частям.
>with(student):
f := x -> arctan(x): u := x -> arctan(x): If := Int(f(x), x):
If = intparts(If, u(x));
|
arctan(x)dx = arctan(x)x − |
x |
|
|
dx |
||
1 + x2 |
|||
>f := x -> x^k*ln(x): u := x -> ln(x):
If := Int(f(x), x):
If = simplify(intparts(If, u(x)));
|
ln(x)x(k+1) |
− |
xkdx |
|
|
|
xk ln(x)dx =
k + 1
Кратные интегралы
В Maple специальных средств для вычисления кратных интегралов не существует. Однако в пакете student есть функции Doubleint и Tripleint, которые позволяют вычислить значение интеграла, если заданы пределы интегрирования. Таким образом, задача сведения кратного интеграла к повторному возлагается на пользователя.
Вычислим xy dΩ , где Ω = (x, y) : 0 ≤ x ≤ 1, x2 ≤ y ≤ x .
Ω
>with(student):
f := (x, y) -> x*y: Doubleint(f(x, y), x, y, Omega) =
value(Doubleint(f(x, y), y=x^2..x, x=0..1)):
53
|
|
|
|
|
yx dx dy = |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
24 |
|
|
|
|
|||
|
|
|
|
Ω |
|
|
|
(x, y) : x2 |
+ y2 |
≤ a2 |
|
Вычислим |
x2 |
+ y2 dΩ , где Ω = |
, |
||||||||
|
Ω |
|
|
|
|
|
|
|
|
|
|
воспользовавшись функцией замены переменных changevar из пакета student.
>f := (x, y) -> sqrt(x^2+y^2):
If := Doubleint(f(x, y), x, y, Omega): sub := {x=r*cos(phi), y=r*sin(phi)}:
If = changevar(sub, If, [r, phi]);
|
|
|
dx dy = |r|2dr dφ |
x2 + y2 |
|||
Ω |
|
Ω |
> If = value(Doubleint(abs(r)^2, r=0..a, phi=0..2*Pi));
|
|
|
|
|
2 |
a3 |
π |
|
x2 |
+ y2 dx dy = |
|||||
|
|
3 |
|
||||
Ω |
|
|
|
|
|
|
|
Криволинейные интегралы
Для вычисления криволинейных интегралов первого рода в пакете student имеется функция Lineint, которая, как и Doubleint и Tripleint, имеет только инертную форму. Параметризация кривой позволяет свести криволинейный интеграл к простому.
Вычислим интеграл y2ds ,
C
где C = (x, y) : x = t − sin t, y = 1 − cos t, 0 ≤ t ≤ 2π .
>with(student):
f := (x, y) -> y^2:
If := Lineint(f(x, y), x, y, t=0..2*Pi):
x := t -> t-sin(t): y := t -> 1-cos(t): If = value(If);
2π |
|
|
|
|
|
|
|
|
|
256 |
||
0 |
1 − cos(t) |
|
2 |
|
1 − cos(t) |
2 |
+ sin(t)2 dt = |
|||||
15 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||
54

4.6Дифференциальные уравнения
Решение обыкновенных дифференциальных уравнений
Maple позволяет решать одиночные дифференциальные уравнения и системы дифференциальных уравнений как аналитически, так и в численном виде. Для решения обыкновенных дифференциальных уравнений используется функция dsolve. Первый параметр функции dsolve должен иметь структуру множества и содержать систему уравнений, а также начальные или краевые условия. Производные при записи дифференциальных уравнений могут задаваться функцией diff или оператором D, однако для записи начальных или граничных условий подходит только оператор D.
Решим сначала уравнение x2 d2y − 3x dy + y = 0 , а затем — задачу dx2 dx
y(1) = 6,
Коши для этого же уравнения с начальными условиями dy
dx(1) = 0 :
>eqn := x^2*(D@@2)(y)(x)-3*x*D(y)(x)+y(x)=0: dsolve(eqn, y(x));
y(x) = _C1 x(2+√3) + _C2 x(2−√3)
>ic := y(1)=6, D(y)(1)=0: dsolve({eqn, ic}, y(x));
|
|
√ |
|
x(2+√ |
|
|
√ |
|
x(2−√ |
|
|
y x |
− 2 |
|
3) |
3) |
|||||||
|
|
||||||||||
( ) = (3 |
|
3) |
|
|
+ (2 |
3 + 3) |
|
|
|||
Решим уравнение, описывающее движение тела, брошенного вверх
на высоте h0 со скоростью v0 :
>eqn := (D@@2)(h)(t)=-g:
ic := h(0)=h[0], D(h)(0)=v[0]: dsolve({eqn, ic}, h(t));
gt2
h(t) = − 2 + v0t + h0
Решим задачу Коши для системы уравнений
c начальными условиями
x(0) = 1, y(0) = 2 :
dx = x + 2y + 2 et,
dt
dy = 2x + y
dt
55
> eqns := D(x)(t)=x(t)+2*y(t)+2*exp(t), D(y)(t)=2*x(t)+y(t):
ic := x(0)=1, y(0)=2:
dsolve({eqns, ic}, {x(t), y(t)});
x(t) = 2 e(3t) − e(−t), y(t) = 2 e(3t) + e(−t) − et
Численное решение дифференциальных уравнений
Для решения дифференциальных уравнений в численном виде используется функция dsolve с параметром numeric. При этом решение возвращается в виде специальной процедуры, которая позволяет найти решение в любой точке или построить график решения. При этом используется функция odeplot из пакета plots.
|
y |
dy |
|
|
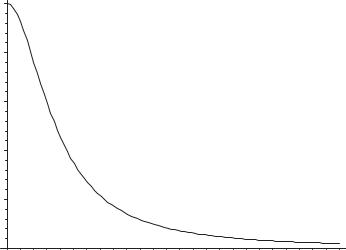
Построим численное решение для задачи Коши |
|
|
= 1 : |
|
(0) |
||||
|
dx |
= −y sin(xy), |
||
>eqn := D(y)(x)=-y(x)*sin(x*y(x)): ic := y(0)=1:
sol := dsolve({eqn, ic}, y(x), numeric): plots[odeplot](sol, [x, y(x)], 0..10, numpoints=100);
1 |
|
|
|
|
|
0.8 |
|
|
|
|
|
0.6 |
|
|
|
|
|
y |
|
|
|
|
|
0.4 |
|
|
|
|
|
0.2 |
|
|
|
|
|
0 |
2 |
4 |
6 |
8 |
10 |
56
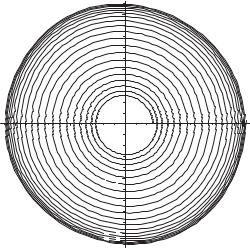
Построим численное решение задачи Коши для уравнения Ван-дер-
d2x |
|
|
dx |
|
x(0) |
= 0.1, |
||||
|
|
|
|
|
dt |
|
||||
Поля dt2 − ε − x2 |
|
|
dt +x = 0 c начальными условиями |
dx |
(0) |
= 0 : |
||||
|
|
|
||||||||
>epsilon := 0.05:
eqn := (D@@2)(x)(t)-(epsilon-x(t)^2)*D(x)(t)+x(t)=0:
ic := x(0)=0.1, D(x)(0)=0:
sol := dsolve({eqn, ic}, x(t), numeric): plots[odeplot](sol, [x(t), -D(x)(t)], 0..40*Pi,
scaling=constrained, numpoints=2500, labels=["", ""]);
|
|
0.4 |
|
|
|
|
0.2 |
|
|
–0.4 |
–0.2 |
0 |
0.2 |
0.4 |
|
||||
|
|
–0.2 |
|
|
|
|
–0.4 |
|
|
57

5Лабораторные работы
5.1Лабораторная работа № 1 «Работа с выражениями»
Вариант № 1
1.Перевести число 10101100011111011100 из двоичной системы в шестнадцате-
ричную.
Ответ: AC7DC.
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
64 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2. |
Вычислить значение выражения |
|
|
|
32√4 + 4 |
√3 |
2 |
|
− 3 |
|
2√4 2 · 3 |
√2. |
|||||||||||||||||||
|
Ответ: 3 |
2 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
Вычислить значение выражения |
|
|
|
x7 + 6x5 |
x=√ |
2 |
|
с точностью до пяти зна- |
||||||||||||||||||||||
|
|
log3 x |
|
||||||||||||||||||||||||||||
|
tg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
ков мантиссы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Ответ: −1.9614. |
9a2 − 4 |
|
|
6a2 − 5a − 6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
4. |
Упростить выражение |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
Ответ: 0. |
2 |
− |
3a − |
|
|
|
3 |
− |
2a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
5.Разложить на множители выражение x4 − 2x3y + x2y2 + x2y − 2xy2 + y3.
Ответ: (x2 + y)(x − y)2.
6.Раскрыть скобки в выражении (x−1)(x2 −1)(x+ 1)(x2 + 1)(x3 + 1) и упорядочить
слагаемые в порядке убывания степеней при переменной x.
Ответ: x9 − x7 + x6 − x5 − x4 + x3 − x2 + 1.
7. |
Разложить дробь |
x3 + 2x − 2 |
|
|
на простейшие составляющие. |
|||||||||||
x3 − 2x2 + x |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
|
4 |
|
1 |
|
|
|
|
|
|
||||
|
Ответ: 1 − |
|
+ |
|
+ |
|
|
|
. |
|
|
|||||
|
x |
x − 1 |
(x − 1)2 |
|
||||||||||||
8. |
Вычислить значение выражения logy z +logz y при условии, что ln y = 2, ln z = 3. |
|||||||||||||||
|
Ответ: |
13 |
. |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k + 2 |
|
||||
9. |
Вычислить произведение |
k=1 |
с точностью до трёх знаков мантиссы. |
|||||||||||||
|
|
|||||||||||||||
k + 1 |
||||||||||||||||
|
Ответ: 7.14. |
|
|
! |
|
|
|
|
|
|
||||||
58

Вариант № 2
1.Перевести число 1BC23 из шестнадцатеричной системы в двоичную.
Ответ: 11011110000100011.
2. |
Вычислить значение выражения 417 · |
2 |
+ |
13 |
|
: |
4 |
+ |
21 |
|
|||||
|
|
|
|
|
|
|
|||||||||
10 |
990 |
10 |
990 |
||||||||||||
|
Ответ: 211. |
sin 2(arcsin x − arccos x) x= 35 |
|||||||||||||
3. |
трёх знаков мантиссы. |
||||||||||||||
|
Вычислить значение выражения |
|
|
|
|
|
|
|
|
|
|
|
√ |
|
|
Ответ: 0.221.
.
с точностью до
4. Упростить выражение
y
Ответ: x + y .
|
x |
− y |
|
x − y |
|
||||||||
√ |
|
− |
√ |
|
|
− √ |
|
+ √ |
|
|
|||
x |
x |
|
|||||||||||
y |
y |
|
|||||||||||
|
x + y |
|
x + y |
|
|||||||||
√x |
− |
√y |
|
+ √x + √y |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
√xy · x − y .
5.Разложить на множители выражение x3 − 5x2 + 3x + 9.
Ответ: (x + 1)(x − 3)2.
6.В выражении y3 +8x2y3 +5xy2 +xy−5y+1 сгруппировать слагаемые по степеням
переменной x.
Ответ: 8y3x2 + (5y2 + y)x + y3 + 1 − 5y.
7. |
Привести к общему знаменателю |
|
2x |
|
|
x − 9 |
. |
|
|
|||||||||||
x − 1 |
|
|
||||||||||||||||||
|
Ответ: |
|
|
|
x |
2 |
− 9 |
. |
|
|
|
− x − 5 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
(x − 1)(x − 5) |
|
|
|
|
|
|
|
|
при условии, что tg x = √ |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
8. |
Вычислить значение выражения |
cos 2x − sin 4x |
|
. |
||||||||||||||||
3 |
||||||||||||||||||||
|
|
√ |
|
|
− 1 . |
|
|
|
|
sin 2x − cos 4x |
||||||||||
|
|
3 |
|
|
|
|
||||||||||||||
|
Ответ: √3 + 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
1000 |
1 |
|
с точностью до семи знаков мантиссы. |
|||||||||
9. |
Вычислить сумму ряда |
√ |
|
|||||||||||||||||
|
||||||||||||||||||||
|
Ответ: 61.80101. |
=1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
i |
i |
|
|
|
|
|
|
|
|
|
|||||||||
59

Вариант № 3
1.Преобразовать число 1.234567 в дробь.
Ответ: 12345671000000 .
2. Вычислить значение выражения |
|
|
1 |
|
|
|
|
|
|
|
. |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
3 + |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
1 + |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
1 + |
|
|
|
|
|
|
|
|
|||||
|
7 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Ответ: |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3. Задать функцию f (x) = |
sin x − cos x |
|
|
и вычислить значение f |
π |
с точностью |
|||||||||||||||
|
|
|
|
||||||||||||||||||
до двух знаков мантиссы. |
cos 2x |
|
|
|
|
|
|
|
|
|
8 |
|
|
||||||||
Ответ: −0.76. |
x3 − y3 |
|
|
|
|
|
|
|
|
|
(x + y2)(x2 + y) − xy(xy + 1) |
|
|||||||||
4. Упростить выражение |
|
|
|
|
|
+ |
|
|
|
. |
|||||||||||
(3x + y)2 − 8x2 − 5xy |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
x2 − xy + y2 |
|||||||||||||
Ответ: 2x.
5.Разложить на множители выражение x4 + 2x3y − xy3 − 2y4.
Ответ: (x2 + xy + y2)(x − y)(x + 2y).
6.Раскрыть скобки в выражении (x + 1)(x2 − 1)(x2 − x + 1)(x3 + 2) и упорядочить
слагаемые в порядке убывания степеней при переменной x.
Ответ: x8 − x6 + 3x5 − 3x3 + 2x2 − 2.
7. |
Привести к общему знаменателю |
2 |
2 |
|
x |
|
y |
||||||||||||||||
|
|
|
|
− |
|
+ |
|
− |
|
. |
|||||||||||||
|
x |
y |
y2 |
x2 |
|||||||||||||||||||
|
Ответ: |
|
x3 − 2x2y + 2xy2 − y3 |
. |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
x2y2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
8. |
Вычислить значение выражения |
logy 4z + logz 2y при условии, что ln y = 3, |
|||||||||||||||||||||
|
ln z = 6. |
|
1 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
|
ln 2 + |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
10 |
|
|
k − 1 |
|
|
с точностью до трёх знаков мантиссы. |
||||||||||||
9. |
Вычислить сумму ряда |
|
|
|
|||||||||||||||||||
k + 1 |
|||||||||||||||||||||||
|
Ответ: |
|
|
|
|
|
k=1 |
|
|
|
|
|
|
|
|||||||||
|
7.27. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
60
