КМ - Maple

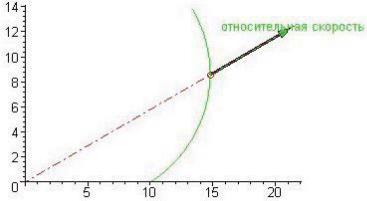
v1[’x’] := V_отн*cos(phi(1/8)): v1[’y’] := V_отн*sin(phi(1/8)):

> display(pos(phi(1/8), S(1/8), 3/16), plottools[arrow]([x, y],

vector([v1[’x’],v1[’y’]]),

.15, .6, .13, color=green), textplot([x+v1[’x’]+dxy, y+v1[’y’]+dxy,

‘относительная скорость‘], color=green),

scaling=constrained);

Стрелка-направление указывает на относительную скорость. Переносная скорость — это скорость той точки подвижного про-

странства (тела D ), с которой совпадает движущая точка. Значит, чтобы найти переносную скорость, необходимо «заморозить» относительное движение, тогда

Vпер = ωh,

где ω — угловая скорость вращения тела D , h — расстояние до оси вращения.

>omega := unapply(diff(phi(t), t), t);

ω:= t −→ 4 + 3.2t

>V_пер := omega(1/8)*S(1/8)/V_размер:

>v2[’x’] := V_пер(1/8)*cos(Pi/2+phi(1/8)): v2[’y’] := V_пер(1/8)*sin(Pi/2+phi(1/8)):

>display(pos(phi(1/8), S(1/8), 3/16), plottools[arrow]([x, y],

vector([v2[’x’], v2[’y’]]),

.15, .6, .1, color=blue), textplot([x+v2[’x’]+dxy, y+v2[’y’]+dxy,

‘переносная скорость‘], color=blue), scaling=constrained);

101

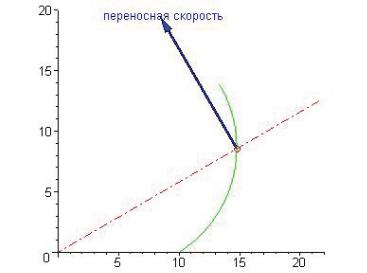
Стрелка-направление указывает на переносную скорость.

Сумма переносной и относительной скоростей есть скорость точки в абсолютном движении. Эта скорость направлена по касательной к траектории.

> display(pos(phi(1/8), S(1/8), 3/16), plottools[arrow]([x, y],

vector([v2[’x’], v2[’y’]]),

.15, .6, .1, color=blue), textplot([x+v2[’x’]+dxy, y+v2[’y’]+dxy,

‘переносная скорость‘], color=blue), plottools[arrow]([x, y],

vector([v1[’x’], v1[’y’]]),

.15, .6, .1, color=green), textplot([x+v1[’x’]+dxy, y+v1[’y’]+dxy,

‘относительная скорость‘], color=green),

plottools[arrow]([x, y], vector([v1[’x’]+v2[’x’],

v1[’y’] + v2[’y’]]),

.15, .6, .1, color=red), textplot([x+v1[’x’]+v2[’x’]+dxy,

y+v1[’y’]+v2[’y’]+dxy, ‘Абсолютная скорость‘], color=red),

scaling=constrained);

102

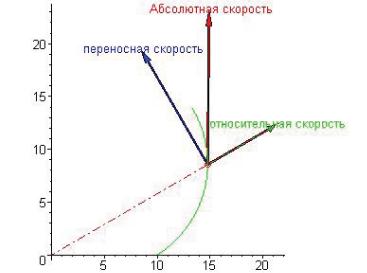
Центральная стрелка указывает на абсолютную скорость. Ближе к оси ординат расположена переносная скорость, а к оси абсцисс — относительная.

>V_абс[’x’] := V_размер*evalf(v1[’x’]+v2[’x’]): V_абс[’y’] := V_размер*evalf(v1[’y’]+v2[’y’]): V_abs := sqrt(V_абс[’x’]^2+V_абс[’y’]^2);

V _abs := 87.26877071

Направляющие косинусы найдем по формулам:

>alpha := V_абс[’x’]/V_abc:

>beta := V_абс[’y’]/V_abc:

Абсолютное ускорение точки есть векторная сумма трех ускорений: относительного, переносного и Кориолиса:

¯ = ¯ + ¯ + ¯

Wабс Wот Wпер Wкор.

Относительное ускорение — это ускорение, возникающее при относительном движении, т.е. при движении точки вдоль тела. Так как точка движется вдоль тела по прямой, то и относительное ускорение направлено вдоль этой прямой.

> W := unapply(diff(S(t), t, t), t);

W := t −→ −40 sin 2πt · π2

103

>W_размер := 20:

>W_отн := W(1/8)/W_размер: w1[’x’] := W_отн*cos(phi(1/8)): w1[’y’] := W_отн*sin(phi(1/8)):

>display(pos(phi(1/8), S(1/8), 3/16), plottools[arrow]([x, y],

vector([w1[’x’], w1[’y’]]),

.15, .6, .1, color=green), textplot([x+w1[’x’]+dxy, y+w1[’y’]+dxy,

‘относительное ускорение‘], color=green),

scaling=constrained);

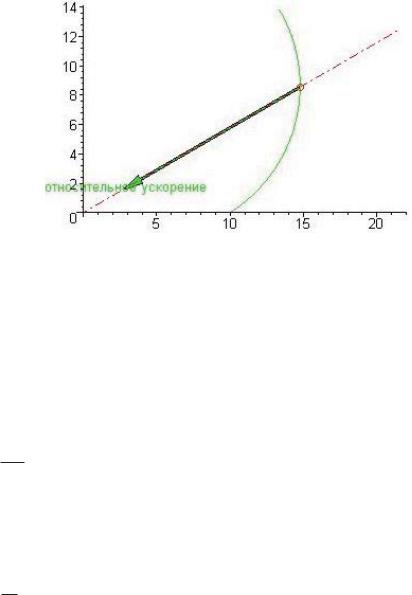
Стрелка-направление указывает на относительное ускорение. Переносное ускорение — это ускорение того места подвижного про-

странства, с которым совпадает движущаяся точка. Следовательно, «замораживаем» относительное движение, а поскольку переносное движение — это вращение тела D по закону ϕ(t) = 4t + 1.6t2 , то переносное ускорение складывается из вращательного и центростремительного.

Wвр = εh,

d2

где: ε = dt2 ϕ(t) — угловое ускорение в данный момент времени, а h =

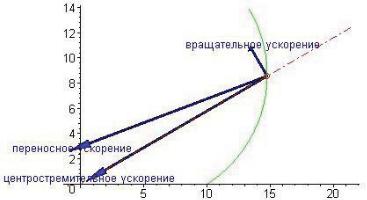
= S(t) — расстояние до оси вращения в данный момент времени. Направлено вращательное ускорение перпендикулярно OM (туда,

куда «укажет» ε ):

Wц = ω2h,

d

где: ω = dtϕ(t) — угловая скорость вращения тела в данный момент. Направлено центростремительное ускорение к оси вращения.

104

>epsilon := unapply(diff(phi(t), t, t), t);

ε= 3.2

>W[‘вр‘] := epsilon(1/8)*S(1/8)/W_размер: W[‘ц‘] := omega(1/8)^2*S(1/8)/W_размер:

>w21[’x’] := W[’вр’]*cos(phi(1/8)+Pi/2): w21[’y’] := W[’вр’]*sin(phi(1/8)+Pi/2): w22[’x’] := W[’ц’]*cos(phi(1/8)+Pi): w22[’y’] := W[’ц’]*sin(phi(1/8)+Pi): w2[’x’] := w21[’x’]+w22[’x’]:

w2[’y’] := w21[’y’]+w22[’y’]:

>display(pos(phi(1/8), S(1/8), 3/16), plottools[arrow]([x, y],

vector([w21[’x’], w21[’y’]]),

.15, .6, .1, color=blue), textplot([x+w21[’x’]+dxy, y+w21[’y’]+dxy,

‘вращательное ускорение‘], color=blue),

plottools[arrow]([x, y],

vector([w22[’x’], w22[’y’]]),

.15, .6, .1, color=blue), plottools[arrow]([x, y],

vector([w2[’x’], w2[’y’]]),

.15, .6, .1, color=blue), textplot([x+w2[’x’]+dxy, y+w2[’y’]+dxy,

‘переносное ускорение‘], color=blue), textplot([x+w22[’x’]+dxy, y+w22[’y’]+dxy,

‘центростремительное ускорение‘], color=blue),

scaling=constrained);

105

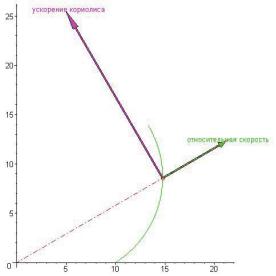
Кориолисово ускорение возникает, когда есть вращательное движение подвижной системы координат, и при этом вектор угловой скорости не коллинеарен вектору скорости относительной.

Кориолисово ускорение равно удвоенному векторному произведению вектора угловой скорости вращения тела и вектора относительной скорости, поэтому величину ускорения Кориолиса определим по формуле

Wкор = 2ωVотн sin γ,

а направление по правилу Жуковского: «Вектор ускорения Кориолиса будет направлен в ту сторону, куда "укажет" вектор относительной скорости, если его повернуть на прямой угол градусов по ходу вращения, показанного угловой скоростью».

>W[‘кор‘] := 2*omega(1/8)*V_отн/W_размер*V_размер:

>w3[’x’] := W[‘кор‘]*cos(phi(1/8)+Pi/2): w3[’y’] := W[‘кор‘]*sin(phi(1/8)+Pi/2):

>display(pos(phi(1/8), S(1/8), 3/16), plottools[arrow]([x, y],

vector([w3[’x’], w3[’y’]]),

.15, .6, .1, color=magenta), textplot([x+w3[’x’]+dxy, y+w3[’y’]+dxy,

‘ускорение кориолиса‘], color=magenta),

plottools[arrow]([x, y],

vector([v1[’x’], v1[’y’]]),

.15, .6, .1, color=green), textplot([x+v1[’x’]+dxy, y+v1[’y’]+dxy,

‘относительная скорость‘], color=green),

scaling=constrained);

106

Ближе к оси OY — ускорение Кориолиса. Вторая стрелка-направ- ление — относительная скорость.

>w_абс[’x’] := evalf(w1[’x’]+w2[’x’]+w3[’x’]): w_абс[’y’] := evalf(w1[’y’]+w2[’y’]+w3[’y’]): w_abs := sqrt(w_абс[’x’]^2+w_абс[’y’]^2);

w_abs := 37.75692035

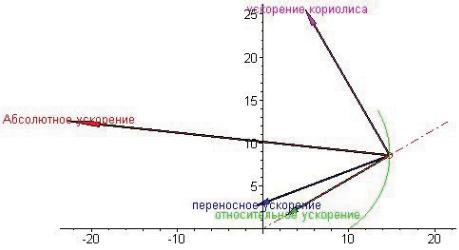
Изобразим три вектора ускорения (относительное переносное и Кориолиса) и их сумму, которая есть ускорение точки в абсолютном движении.

> display(pos(phi(1/8), S(1/8), 3/16), plottools[arrow]([x, y],

vector([w2[’x’], w2[’y’]]),

.15, .6, .1, color=blue), textplot([x+w2[’x’]+dxy, y+w2[’y’]+dxy,

‘переносное ускорение‘], color=blue),

plottools[arrow]([x, y],

vector([w1[’x’], w1[’y’]]),

.15, .6, .1, color=green), textplot([x+w1[’x’]+dxy, y+w1[’y’]+dxy,

‘относительное ускорение‘], color=green),

plottools[arrow]([x, y],

vector([w3[’x’], w3[’y’]]),

.15, .6, .1, color=magenta), textplot([x+w3[’x’]+dxy, y+w3[’y’]+dxy,

‘ускорение кориолиса‘], color=magenta),

plottools[arrow]([x, y], vector([w_абс[’x’],

w_абс[’y’]]),

.15, .6, .1, color=red), textplot([x+w_абс[’x’]+dxy, y+w_абс[’y’]+dxy,

‘Абсолютное ускорение‘], color=red), scaling=constrained);

107

Ответ

>‘Положение точки‘; ’S’ = evalf(S(1/8));

’phi’ = evalf(convert(phi(1/8), degrees)); ‘Угловая скорость тела и угловое ускорение тела‘; ’omega’ = omega(1/8);

’epsilon’ = epsilon(1/8); ‘Абсолютная скорость точки‘; V[’абс,x’] = V_абс[’x’]; V[’абс,y’] = V_абс[’y’]; V[’абс’] = V_abs;

‘Абсолютное ускорение точки‘; W[’абс,x’] = W_размер*w_абс[’x’]; W[’абс,y’] = W_размер*w_абс[’y’]; W[’абс’] = W_размер*w_abs;

Положение точки:

S = 17.07106781

ϕ = 30.08028424

Угловая скорость тела и угловое ускорение тела:

ω= 4.400000000

ε= 3.2

Абсолютная скорость точки:

Vабс,x = 0.797868516

Vабс,y = 87.26512332

Vабс = 87.26877071

Абсолютное ускорение точки:

Wабс,x = −750.8861962

Wабс,y = 80.02458420

Wабс = 755.1384070

108

6.3Применение интегралов для функций многих переменных

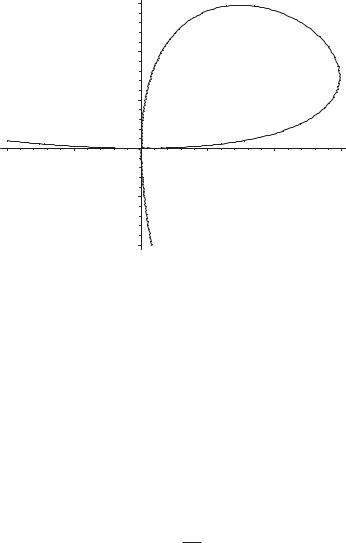
Пример № 1

Найти площадь петли кривой (x + y)3 = a xy .

Решение

>restart;

>with(student):

with(plots):

>L := (x+y)^3=a*x*y: a := 10:

implicitplot(L, x=-1..a, y=-1..a, numpoints=100000); a := ’a’:

>tr := x=rho*cos(phi), y=rho*sin(phi):

eq_rho := collect(subs(tr, L) / rho^2, rho): eq_rho;

rho[0] := factor(solve(eq_rho, rho));

>with(Student[MultivariateCalculus]):

>S := MultiInt(1, rho=0..rho[0], phi=0..Pi/2,

coordinates=polar[rho,phi]):

’S’ = S;

S =

a2

60

109

Пример № 2

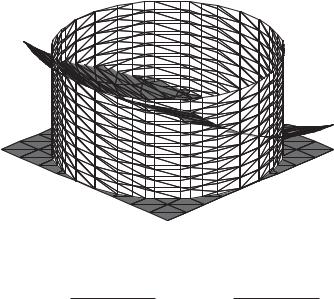
Найти площадь поверхности x2 + y2 = 2ax , если 0 az x2 + y2 , a > 0 .

Решение

>restart;

>with(plots):

>P := x^2+y^2=2*a*x: D := a*z=x^2+y^2:

>a := 1:

F := implicitplot3d(P, x=0..2*a, y=-a..a, z=0..4*a,

color=white):

G := implicitplot3d(z=0, x=0..2*a, y=-a..a, z=0..4*a, color=red):

H := implicitplot3d(D, x=0..2*a, y=-a..a, z=0..4*a, color=red):

display({F, G, H}); a := ’a’:

>Y := solve(P, y): y=Y[1], y=Y[2];

y = −x2 + 2ax, y = − −x2 + 2ax

>Z := solve(subs(y=Y[1], C), z): z=Z;

f := sqrt(1+diff(Y[1],x)^2+diff(Y[1],z)^2):

z = 2x

110