Простейшие помехоустойчивые коды

Код с постоянным весом - несистематический код, каждое разрешающее слово которого имеет постоянное количество единичных символов (постоянный вес). Широкое применение на практике получил семиэлементный код с весом 3, каждая комбинация которого содержит 3 единицы и 4 нуля. Этот код используется для передачи дискретных сообщений по коротковолновым каналам связи и известен как международный телеграфный код №3 (МТК 3). Из общего числа комбинаций семиэлементного кода Nn=27=128, число разрешенных составляет Np=7!/3!(7-3)!=35. Коэффициент избыточности кода Ки=1-log235/log2128 = 0,26, а минимальное кодовое расстояние dmin=2. При приеме кодовых комбинаций производится подсчет числа единиц в кодовом слове, что позволяет обнаруживать ошибки нечетной кратности. Применение кода с постоянным весом целесообразно в асимметричных каналах (например, каналы с АМн при неоптимальном пороге). Коды Бергера или коды с суммированием относятся к разряду нелинейных кодов. Они также предназначены для использования в асимметричных каналах связи. Вариант кодирования: в информационной части кодовой комбинации подсчитывается число единиц, после чего формируются проверочные элементы, представляющие запись этого числа в двоичной форме. Таким же образом формируются проверочные элементы на приемной стороне и сравниваются с принятыми проверочными. Минимальное кодовое расстояние dмин=2. Повышение достоверности с помощью кодов Бергера дает приблизительно такие же результаты, как использование кода МТК-3, однако важным достоинством кода Бергера является разделения кодовых символов на информационные и проверочные, что упрощает построение кодирующих и декодирующих устройств. Код с проверкой на четность Независимо от длины кодовой комбинации этот код имеет один проверочный элемент и обозначается как (n,n-1) - код. Значение проверочного элемента выбирается из условия получения четного числа единиц, т.е. общее число единиц в любом разрешенном кодовом слове четное. Этот код имеет dмин=2 и обнаруживает все ошибки нечетной кратности. Если в качестве первичного используется код МТК-2 (n=5), то n=6, r=1. Коэффициент избыточности Ки=0,17, что частично объясняет низкую эффективность кода. Существует также код с двумя проверками на четность. Независимо от длины кодовой комбинации этот код имеет два проверочных элемента, один из которых выбирается из условия четности всех информационных разрядов, а второй - из условия четности всех нечетных (или четных) по номеру информационных разрядов. Этот код обнаруживает часть ошибок четной кратности - все смежные, рядом расположенные ошибки. Коды с повторением  - коды, в которых один заданный информационный символ повторяется n раз (обычно n нечетно) и поэтому считается  низкоскоростным. Код с повторением имеет длину n=nk, минимальное кодовое расстояние dмин=n.   Избыточность кода равна (n-1)/n. Код с повторением характеризуется довольно высокими исправляющими свойствами при действии пакетов ошибок. Так при n=2 всегда исправляются пакеты ошибок до n/2. Недостатком кодов с повторением является весьма высокая избыточность. Даже при двукратном повторении коэффициент избыточности равен 0,5.

Коды   Боуза-Чоудхури-Хоквингейма (коды БЧХ) Коды БЧХ - циклические n-элементные коды. Разработаны для увеличения минимального кодового расстояния и повышения корректирующей способности. Длина кодовой комбинации в них  n=2r+1-1 (т.о. кодовая комбинация может содержать 3, 7, 15, 31, 63, 127). Порождающий полином находится как наименьшее общее кратное (НОК) неприводимых полиномов Mi(x), i=1,m, где m£dmin-2. (Полином называют неприводимым, если он делится без остатка только на единицу и на самого себя. Наименьшим общим кратным совокупности неприводимых полиномов называют полином с наименьшим показателем степени, который делится на каждый из них.) Коды БЧХ обладают хорошими корректирующими способностями и позволяют обнаруживать и исправлять ошибки с учетом группирования, что очень важно для реальных каналов. При этом они обладают нечетными значениями минимального кодового расстояния. Циклические коды БЧХ получили применение в аппаратуре передачи данных. Существует рекомендации МККТТ, согласно которой в среднескоростных системах передачи данных предлагается применять коды БЧХ с dmin=4 и n=260; 500; 980 разрядов. Порождающий полином этих кодов Р(х)=х16+х12+х5+1. Многочисленные испытания кодов БЧХ  подтвердили их высокую эффективность: при передаче данных по коммутируемым каналам телефонной сети общего пользования с ро>10-3, вероятность не обнаруживаемой ошибки при приеме 8-разрядных знаков (байтов), из которых составлена информационная часть кодовой комбинации, не превышает  10-6.

Под пропускной способностью понимается теоретически достижимая, наибольшая скорость передачи информации.

Основные характеристики

1. Минимальное кодовое расстояние (dmin) есть наименьшее из кодовых расстояний всех возможных пар комбинаций данного кода. (Для первичных кодов (не помехоустойчивых) dmin=1). Минимальное кодовое расстояние  определяет способность кода обнаруживать и исправлять ошибки различной кратности в принятом слове. Число обнаруживаемых и исправляемых ошибок связано с минимальным кодовым расстоянием следующими соотношениями s£ dmin -1,    t£ (dmin -1)/2,                                                      (3.1) где s - число обнаруживаемых ошибок, t - число исправляемых ошибок. Для любого (n,k)-кода с минимальным расстоянием, не меньшим 2t+1 число проверочных символов определяется: . При dmin=3 r=log2(n+1)=log2(r+k+1).                                         (3.2) Коды, для которых выполняется равенство (3.2) называются совершенными. 2. Коэффициент  избыточности Ки  - показатель степени удлинения кодовых слов для достижения заданной помехоустойчивости кода ,                                                           (3.3) где Nn - общее число кодовых комбинаций. Для систематических (n,k) - кодов     Nn=2n  и   Nk=2k. Поэтому . 3. Вероятность необнаруживаемой ошибки Рно есть вероятность выдачи декодером ошибочного кодового слова.  - вероятность наличия в n - элементном кодовом слове ошибки кратности t и более. Учитывая то, что ошибки в канале могут быть описаны биномиальным распределением, то для кодов исправляющих ошибки кратности t: 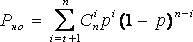,                                                 (3.4) а для кодов обнаруживающих ошибки кратности s: ,                                             (3.5) где р - вероятность появления i ошибок. 4. Коэффициент повышения достоверности Кпд показывает во сколько раз уменьшается вероятность появления ошибочных кодовых комбинаций на выходе декодирующего устройства по сравнению с вероятностью ошибочного приема кодовой комбинации в канале связи. Для кодов обнаруживающих ошибки коэффициент повышения достоверности равен .                                                           (3.6) Так как P(³1,n)/P(³dmin,n) всегда больше 1, то Кпд>2r. Для большинства кодов величина 2r является оценкой снизу коэффициента повышения достоверности. На основании определения вероятности необнаруживаемой ошибки и коэффициента повышения достоверности можно оценить эффективность использования избыточного кодирования.

Исследование информационных систем, описанных в виде параллельных агрегативных систем. Системы массового обслуживания, состоящие из бесконечного множества приборов. Предельное поведение системы массового обслуживания с бесконечно возрастающим числом приборов и загрузкой, стремящейся к критической.

Методика построения помехоустойчивых кодов. Информационный предел избыточности

Кодирование с помощью которого можно устранять ошибки обусловленные наличием шума в канале называется помехоустойчивым. Коды способные исправлять и обнаруживать ошибки называется помехоустойчивым кодом. К сожалению основная теорема кодирования Шеннона не конструктивна, она не указывает способ построения конкретного оптимального помехоустойчивого кода, обеспечивающего предельное согласование сигнала с каналом, существование которого доказывает. Вместе с тем обосновав принципиальную возможность построения помехоустойчивых кодов, обеспечивающих идеальную передачу. Теория Шеннона мобилизовала усилия ученых на разработку конкретных кодов. В результате в настоящее время теория помехоустойчивого кодирования превратилась в самостоятельную науку в развитии которой достигнуты большие успехи. Рассмотрим основополагающие принципы заложенные в основу построения помехоустойчивых кодов. Как следует из доказательства основной теоремы Шеннона неприменимым свойством помехоустойчивых кодов является наличие избыточности. При этом необходима не просто любая избыточность, а специфическая, определяемая свойствами канала и правилом построения кода. И позволяющая с минимальными затратами повысить вероятность передачи. В ситуации когда источник сообщений обладает собственной существенной избыточностью, которая в принципе тоже в определенной степени повышает достоверность передачи информации, но не так эффектно как это возможно. Поступают следующим образом: сначала с помощью эффективного кодирования до минимума уменьшают избыточность источника сообщений, а затем в процессе помехоустойчивого кодирования вносят в передаваемый сигнал избыточность, позволяющую простыми средствами поднять верность. Таким образом эффективное кодирование может сочетаться с помехоустойчивым. Помехоустойчивые коды можно подразделить на два больших класса блочные и непрерывные. В случае блочных кодов, при кодировании, каждому дискретному сообщению ставится в соответствие отдельный блок кодовых символов называемого кодовой комбинацией. Непрерывные коды образуют последовательность символов неразделяемых на кодовые комбинации. Рассмотрим принцип построения помехоустойчивых блочных кодов. Избыточность обуславливающая корректирующие свойства равномерного блочного кода обычно вводится за счет выполнения неравенства mn M (2.29), где m-основание кода т.е. объем алфавита используемых кодовых символов, n-длина или количество разрядов кодовой комбинации, М-количество сообщений подлежащих кодированию. Выполнение этого неравенства означает, что для передачи знаков сообщения используют лишь часть М возможных кодовых комбинаций. Используемые кодовые комбинации называют разрешенными. Неиспользуемые mn -M комбинации являются запрещенными. На вход канала подаются только разрешенные комбинации. Если вследствие помех один или несколько символов приняты ошибочно, то на выходе канала появляется запрещенная комбинация, что и говорит о наличии ошибки. Для того, чтобы обеспечить выполнение (2.29) необходимо выбирать n  K , где К-минимальное целое, удовлетворяющее неравенству mKM (2.30). Число К обычно называют количеством информационных разрядов кодовой комбинации, поскольку именно столько разрядов должна содержать комбинация кода с основанием m, чтобы число разных кодовых комбинаций было не меньше числа сообщений М подлежащих передаче. R=n-K разрядов кодовой комбинации необходимых для передачи полезной информации называются проверочными. Количество их и определяет избыточность помехоустойчивого кода. При использовании помехоустойчивого кода возможно декодирование с обнаружением и исправлением ошибок. В первом случае на основе анализа принятой комбинации выясняется, является ли она разрешенной или запрещенной. После этого запрещенная комбинация либо отбрасывается, либо уточняется путем посылки запроса на повторение переданной информации. Во втором случае при приеме запрещенной комбинации определенным способом выявляются и исправляются содержащиеся в ней ошибки. Максимальные числа ошибок в кодовой комбинации q и S которые могут быть обнаружены (q) или исправлены (S) с помощью данного кода называются соответственно обнаруживающей или исправляющей способностью кода. В значении q и S определяются величиной dmin минимальным кодовым расстоянием между ближайшими разрешенными комбинациями. Под кодовым расстоянием понимают количество неодинаковых разрядов в кодовых комбинациях. Величина dmin в помехоустойчивом коде зависит от соотношения n и К т.е. от числа r проверочных разрядов кода. Рассмотрим информационный (т.е. базирующий на идеях Теории Информации) подход позволяющий оценить необходимую минимальную избыточность, выраженную в количестве проверочных разрядов rmin блочного помехоустойчивого кода длиной n с заданной исправляющей способностью S. Пусть имеется код с основанием m и с исправляющей способностью S. И используется декодирование с исправлением ошибок. На приеме при использовании такого кода возможно две ситуации: правильный прием сообщения и неправильный. Осуществление с вероятностью PH. Неправильный прием может произойти в том случае, когда из-за превышения числом ошибок пришедшей из канала кодовой комбинации значение S она может превратиться в одну из других разрешенных кодовых комбинаций. В свою очередь правильный прием осуществляется либо в том случае, когда в принимаемой комбинации отсутствуют ошибки (обозначим вероятность такого сообщения Р0), либо Nправ в случаях когда в принятой комбинации присутствуют ошибки которые могут быть исправлены рассмотренным кодом. Вероятности таких случаев обозначим через Pj j=1  Nправ. Для решения поставленной задачи определим минимальное количество информации, которой может быть описана совокупность событий, включающая появление одной из конкретных ошибок и отсутствие ошибок или появление некорректных ошибок. Зная эту величину и максимальное количество информации которое может содержать один проверочный символ кода можно определить минимальное число проверочных символов. Количество информации необходимо для описания указанных событий (2.31) (в случае отсутствия ошибки учтем включением нуля в предел суммирования). Максимальное количество информации которое может содержать символ кода с основанием m в соответствии с (1.6) равно log2m. Следовательно число проверочных разрядов в комбинации кода не может быть меньше, чем (2.32). Определенную таким образом величину rmin называют информационным пределом избыточности. Найдем значение rmin для двоичного канала с независимыми ошибками. В таком канале появление предыдущей ошибки не влечет за собой появление последующей. В этой ситуации число R(i) ошибок кратности i в кодовой комбинации длиной n равно числу сочетаний .

(2.33).

Поскольку ошибки независимы вероятность P(i) возникновения в кодовой комбинации ошибки кратности i равна P(i)=Pi(1-P)n-i (2.34), где Р-вероятность ошибки в канале. Учитывая, что в данном случае Nпр=S выражение (2.31) можно записать в виде . Вторым слагаемым можно пренебречь поскольку, описываемая им функция не используется в процессе исправления ошибок. Поэтому с учетом (2.23 и 2.24) имеем (2.35). Рассмотрим частный случай когда возникновение конкретной ошибки любой кратности и отсутствие ошибок имеют равную вероятность, т.е. Pi(1-P)n-i=P1 при любом i. Величину Р1 определим из условия нормировки (2.36), отражающего тот факт, что вероятность появления ошибки какой-либо кратности, включения и нулевую равна единице. Из (2.36) имеем 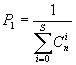следовательно (2.37). Поскольку под двоичной, то есть m=2 c учетом (2.37 и 2.38) имеем . Найденное таким образом значение rmin совпадает с оценками полученными другим методами в частности с нижним пределом Хэмминга. Аналогичным образом могут быть найдены информационные пределы избыточности для других конфигураций ошибок в канале, например для пакетных ошибок, когда одиночные ошибки группируются в пакеты различной кратности. Полученные при этом результаты так же хорошо согласовывается с выводами полученными другими методами. Найденное таким образом значение rmin совпадает с оценками, полученными другими методами, в частности, с нижним пределом Хэмминга. Аналогичным образом могут быть найдены информационные пределы избыточности для других конфигураций ошибок в канале, например для пакетных ошибок, когда одиночные ошибки группируются в пакеты различной кратности. Получаемые при этом результаты также хорошо согласуются с выводами, полученными другими методами.

Информатика Помехоустойчивые коды и их основные параметры Цифровые сети для передачи речи и данных

Агрегатное описание информационных систем. Понятие агрегата. Операторы входов и выходов. Обрывающийся случайный процесс. Случайный поток. Агрегат как случайный процесс. Кусочно-марковский агрегат. Последовательное раскрытие элементарного события. Кусочно-непрерывные и кусочно-линейные агрегаты. Приведение кусочно-линейных и кусочно-непрерывных агрегатов к каноническому виду.