[Править] * Теоретический предел

(theory) В примечании к задаче (task:errmod) было указано как можно получить значение коэффициента содержания полезной информации (КПС) на один бит, если передавать данные по каналу с шумом p словами длиной n бит, при условии, чтобы вероятность незамеченной ошибки была меньше P_miss.

Но ясно, что указанная там функция дает лишь оценку снизу оптимального значения КПС — возможно, существует другие методы контролирования ошибок, для которых он выше. Теория информации позволяет нам найти точное значение этого коэффициента.

Сформулируем задачу о кодировании, обнаруживающем ошибки. Для начала предположим, что наличие ошибки фиксируется с абсолютной точностью.

Задача 6.

(task:err) Мы хотим передавать информацию блоками, которые содержали бы m бит полезной информации, так, чтобы вероятность ошибки в одном бите равнялась p, а правильность передачи «фиксировалось контрольной суммой». Найти минимальный размер блока n(m,p) и коэффициент раздувания .

Конец задачи.

Решение. Для передачи m бит с вероятностью ошибки в отдельном бите p требуется передать mC(p) бит (см. задачу (task:dual)). Кроме того мы хотим сообщать об ошибке в передаче. Её вероятность равна (1 − p)^m, а значит информация, заложенная в этом сообщении, H((1 − p)^m). В итоге получаем n = mC(p) + H((1 − p)^m) и

Конец решения.

Заметим, что k(1,p) = 1 — когда блок имеет размер один бит, сообщение об ошибке в нём равносильно передаче самого бита.

Если передавать эти сообщения по каналу с уровнем помех p, то количество бит на одно сообщение равно mk(m,p) / C(p), то есть теоретическая оценка для количества лишних бит равна

Понятно, что данная теоретическая оценка занижена.

[Править] Коды Хемминга

Элементарный пример кода исправляющего ошибки был показан на странице \pageref{simplecode}. Его обобщение очевидно. Для подобного кода, обнаруживающего одну ошибку, КПС равен . Оказывается это число можно сделать сколь угодно близким к единице с помощью кодов Хемминга. В частности, при кодировании 11 бит получается слово длинной 15 бит, то есть .

Оценим минимальное количество контрольных разрядов, необходимое для исправления одиночных ошибок. Пусть содержательная часть составляет m бит, и мы добавляем ещё r контрольных. Каждое из 2^m правильных сообщений имеет n = m + r его неправильных вариантов с ошибкой в одном бите. Такими образом, с каждым из 2^m сообщений связано множество из n + 1 слов и эти множества не должны пересекаться. Так как общее число слов 2ⁿ, то

Этот теоретический предел достижим при использовании метода, предложенного Хеммингом. Идея его в следующем: все биты, номера которых есть степень 2, — контрольные, остальные — биты сообщения. Каждый контрольный бит отвечает за чётность суммы некоторой группы бит. Один и тот же бит может относиться к разным группам. Чтобы определить какие контрольные биты контролируют бит в позиции k надо разложить k по степеням двойки: если k = 11 = 8 + 2 + 1, то этот бит относится к трём группам — к группе, чья чётность подсчитывается в 1-ом бите, к группе 2-ого и к группе 8-ого бита. Другими словами в контрольный бит с номером 2^k заносится сумма (по модулю 2) бит с номерами, которые имеют в разложении по степеням двойки степень 2^k:

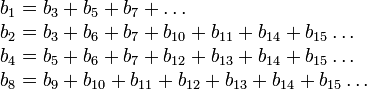(eq:hem)

Код Хемминга оптимален при n = 2^r − 1 и m = n − r. В общем случае m = n − [log ₂(n + 1)], где [x] — ближайшее целое число . Код Хемминга мы будем обозначать Hem(n,m) (хотя n однозначно определяет m).

Пример для Hem(15,11):

Невозможно разобрать выражение (неизвестная функция\fbox): \fbox{10110100111}\to \fbox{\fbox{0}\fbox{0}1\fbox{1}011\fbox{0}0100111}

Невозможно разобрать выражение (неизвестная функция\hphantom): \hphantom{\fbox{10110100111}\to}\;\; \lefteqn{\,b_1}\hphantom{\fbox{0}} \lefteqn{\,b_2}\hphantom{\fbox{0}} \lefteqn{b_3}\hphantom{1} \lefteqn{\;b_4}\hphantom{\fbox{1}011} \lefteqn{\,b_8}\hphantom{\fbox{0}} \lefteqn{b_9}\hphantom{010011} \lefteqn{b_{15}}\hphantom{1}

Получив слово, получатель проверяет каждый контрольный бит на предмет правильности чётности и складывая номера контрольных бит, в которых нарушена чётность. Полученное число, есть XOR номеров бит, где произошла ошибка. Если ошибка одна, то это число есть просто номер ошибочного бита.

Например, если в контрольных разрядах 1, 2, 8 обнаружено несовпадение чётности, то ошибка в 11 разряде, так как только он связан одновременно с этими тремя контрольными разрядами.

\begin{figure}[h!] \psfrag{Check bits}{\hspace{-12mm}Контрольные биты} \centering\includegraphics[clip=true, width=0.65\textwidth]{pictures/hem.eps} \caption{Кодирование Хемминга} (fig:hem) \end{figure}

Задача 7.

Покажите, что при .

Конец задачи.

Код Хемминга может исправлять только единичные ошибки. Однако, есть приём, который позволяет распространить этот код на случай групповых ошибок. Пусть нам надо передать k кодослов. Расположим их в виде матрицы одно слово — строка. Обычно, передают слово за словом. Но мы поступим иначе, передадим слово длины k, из 1-ых разрядов всех слов, затем — вторых и т. д. По приёме всех слов матрица восстанавливается. Если мы хотим обнаруживать групповые ошибки размера k, то в каждой строке восстановленной матрицы будет не более одной ошибки. А с одиночными ошибками код Хемминга справится.