КМ - Maple

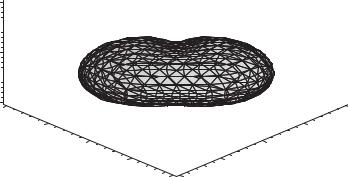
>with(Student[MultivariateCalculus]):

S := 2*MultiInt(f, z=0..Z, x=0..2*a) assuming a>0: ’S’ = S;

S = 4a2π

Пример № 3

Найти объем тела, ограниченного поверхностью (x2+y2+z2)3 = a3(x3+ y3), где a > 0.

Решение

>restart;

>with(plots):

>P := (x^2+y^2+z^2)^3=a^3*(x^3+y^3):

>a := 1:

implicitplot3d(P, x=-a..a, y=-a..a, z=-a..a,

numpoints=6000, axes=frame);

a := ’a’:

1

0.5

–0.5

11

>tr := x=r*cos(phi)*sin(psi), y=r*sin(phi)*sin(psi), z=r*cos(psi):

eq_r := collect(subs(tr, P) / r^3, r): R := solve(eq_r, r):

r = R[1];

r = a sin ψ cos3 ϕ + sin3 ϕ (13 )

Найдем промежуток, на котором неотрицательна функция cos3 ϕ+

1

+ sin3 ϕ 3 . Для этого определим все действительные корни уравнения

1

cos3 ϕ + sin3 ϕ 3 = 0 :

111

>Phi_sol := {}:

for t in solve(R[1], phi) do if type(t, realcons) then

Phi_sol := Phi_sol union {t}; end if;

end do;

Phi := convert(Phi_sol, list): phi[1] = Phi[1];

phi[2] = Phi[2];

π

φ1 = −4

3π φ2 = 4

>with(student):

Int_V := Tripleint(1, x, y, z):

Int_V := changevar({tr}, Int_V, [r, psi, phi]): V := Tripleint(integrand(Int_V), r=0..R[1],

psi=0..Pi, phi=Phi[1]..Phi[2]): ’V’ = value(V);

√

V = 5 2a3π

24

Пример № 4

Пользуясь формулой Грина, вычислить (замыкая, если нужно, кри-

Решение

>restart;

>P := 4*x*y-15*x^2*y: Q := 2*x-5*x^3+7:

Diff(’P’, y) = diff(P, y); Diff(’Q’, x) = diff(Q, x);

f := diff(Q, x) - diff(P, y):

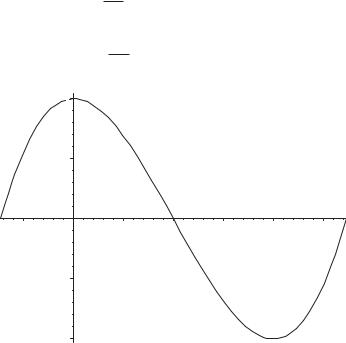
>L := y=x^3-3*x^2+2: a := 1-sqrt(3):

b := 1+sqrt(3): plot(rhs(L), x=a..b);

112

>with(Student[MultivariateCalculus]): In := MultiInt(f, y=0..rhs(L), x=a..1)

+MultiInt(f, y=rhs(L)..0, x=1..b): ’I’ = simplify(In);

I= −9

6.4Решение некоторых задач МСС

Пример № 1. Определение тензора скорости деформации, тензора вихря, скорости относительного изменения объема по заданному полю скоростей

>restart;

>w := array(1..3, [4*x[1]-3*x[3], (x[2]+x[3])^2,

x[2]-x[3]]):

Тензор скорости деформации:

>eps := array(1..3, 1..3): deforscorosty := proc(w)

local i, j; global eps;

for i from 1 to 3 do for j from 1 to 3 do

eps[i,j] := diff(w[i],x[j])+diff(w[j],x[i]);

113

eps[i,j] := 0.5*eps[i,j]; end do;

end do; end proc:

deforscorosty(w):

print(eps);

Тензор вихря:

>omega := array(1..3, 1..3): deforvihrya := proc(w)

local i, j; global omega;

for i from 1 to 3 do for j from 1 to 3 do

omega[i,j] := diff(w[i],x[j])-diff(w[j],x[i]); omega[i,j] := 0.5*omega[i,j];

end do; end do;

end proc: deforvihrya(w):

print(omega);

Скорость относительного изменения объема по заданному полю скоростей:

> eps[1,1]+eps[2,2]+eps[3,3];

3 + 2x2 + 2x3

Тензор скорости деформации:

> x[1] := 2; x[2] := 3; x[3] := 4;

>s := array(x[1]..x[3]): eps(s);

40 −1.5

114

Тензор вихря:

> omega(s);

Скорость относительного изменения объема по заданному полю скоростей:

> eps[1,1]+eps[2,2]+eps[3,3];

17

Пример № 2. Течение под действием перепада давления между цилиндрами, один из которых движется

Между соосными цилиндрами с заданными радиусами под действием известного перепада давления движется вязкая несжимаемая жидкость. Один из цилиндров неподвижен, а второй движется поступательно вдоль своей оси с постоянной скоростью:

1.Внутренний цилиндр неподвижен.

2.Внешний цилиндр неподвижен.

>restart;

Полные уравнения Навье–Стокса, описывающие ламинарное течение вязкой несжимаемой жидкости.

> Diff(v[x],t)+v[x]*Diff(v[x],x)+v[y]*Diff(v[x],y) +v[z]*Diff(v[x],z) = F[x]-(1/rho)*Diff(p,x) +(mu1/rho)*(Diff(Diff(v[x],x),x) +Diff(Diff(v[x],y),y)+Diff(Diff(v[x],z),z));

Diff(v[y],t)+v[x]*Diff(v[y],x)+v[y]*Diff(v[y],y) +v[z]*Diff(v[y],z) = F[y]-(1/rho)*Diff(p,y) +(mu1/rho)*(Diff(Diff(v[y],x),x) +Diff(Diff(v[y],y),y)+Diff(Diff(v[y],z),z));

Diff(v[z],t)+v[x]*Diff(v[z],x)+v[y]*Diff(v[z],y) +v[z]*Diff(v[z],z) = F[z]-(1/rho)*Diff(p,z) +(mu1/rho)*(Diff(Diff(v[z],x),x) +Diff(Diff(v[z],y),y)+Diff(Diff(v[z],z),z));

Diff(v[x],x)+Diff(v[y],y)+Diff(v[z],z)=0;

115

Поскольку область течения является цилиндрической, то рассмотрение соответствующей математической модели целесообразнее проводить в системе координат также цилиндрической (r, ϕ, z) . Полные уравнения Навье–Стокса, описывающие ламинарное течение вязкой несжимаемой жидкости в цилиндрической системе координат, имеют следующий вид:

> Diff(v[r],t)+v[r]*Diff(v[r],r) +(v[phi]/r)*Diff(v[r],phi)+v[z]*Diff(v[r],z) -((v[phi])^2/r) = (-1/rho)*Diff(p,r) +nu*(Diff(Diff(v[r],r),r)+(1/r)*Diff(v[r],r) +(1/r^2)*Diff(Diff(v[r],phi),phi) +Diff(Diff(v[r],z),z)-(v[r]/r^2) -(2/r^2)*Diff(v[phi],phi))+f[r];

Diff(v[phi],t)+v[r]*Diff(v[phi],r)

+(v[phi]/r)*Diff(v[phi],phi)+v[z]*Diff(v[phi],z) +((v[r]*v[phi])/r) = (-1/(rho*r))*Diff(p,phi) +nu*(Diff(Diff(v[phi],r),r)+(1/r)*Diff(v[phi],r) +(1/r^2)*Diff(Diff(v[phi],phi),phi) +Diff(Diff(v[phi],z),z) +(2/r^2)*Diff(v[r],phi)-(v[phi]/r)) + f[phi];

Diff(v[z],t)+v[r]*Diff(v[z],r)

+(v[phi]/r)*Diff(v[z],phi)+v[z]*Diff(v[z],z) = (-1/rho)*Diff(p,z)+nu*(Diff(Diff(v[z],r),r) +(1/r)*Diff(v[z],r) +(1/r^2)*Diff(Diff(v[z],phi),phi) +Diff(Diff(v[z],z),z))+f[z];

Diff(v[r],r)+(v[r]/r)+(1/r)*Diff(v[phi],phi) +Diff(v[z],z) = 0;

В силу стационарности и осесимметричности течения все частные производные по времени и координате phi равны нулю, то есть

>Diff(v[r],t) = 0; Diff(v[phi],t) = 0; Diff(v[z],t) = 0; Diff(v[r],phi) = 0; Diff(v[phi],phi) = 0; Diff(v[z],phi) = 0; Diff(p,phi) = 0;

Поскольку массовые силы не учитываются, то все phi в уравнениях надо положить равными нулю. Предположим, что вектор скорости v параллелен оси z. Тогда он имеет лишь одну компоненту, отличную от нуля, то есть v=(0,0,v[z]) или v[r]=v[phi]=0. В этом случае из уравнения неразрывности непосредственно следует, что

116

> Diff(v[z],z) = 0;

то есть неизвестная величина v[z] не зависит от переменной z и является лишь функцией пространственной координаты r, то есть компонента скорости

> v[z] = v[z](r);

Из двух первых уравнений Навье–Стокса получаем

>Diff(p,r) = 0; p = p(z);

Сучетом вышесказанного запишем третье уравнение

>Diff(Diff(v[z],r),r)+(1/r)*Diff(v[z],r)

=(1/mu)*Diff(p,z);

В обыкновенное дифференциальное уравнение входит две неизвестные функции v=v[r] и p=p[z], зависящие от разных переменных. Следовательно, левая и правая части уравнения должны быть равны некоторой константе, которая определяется с учетом дополнительных условий относительно неизвестной функции p=p[z]. Действительно, если

>Diff(p,z) = c1; Diff(Diff(p,z),z) = 0;

то после его интегрирования находим, что

> p[z]=c1*z+c2;

и для нахождения функции p=p[z] достаточно задать два граничных условия, например,

>z = 0, p(0) = p0; z = l, p(l) = p1; p1 < p0;

c2 = p0;

c1 = (p1-p0)/l; Diff(p,z) = -(p0-p1)/l;

1.Внутренний цилиндр неподвижен:

>Diff(Diff(v[z],r),r)+(1/r)*Diff(v[z],r)

=(1/mu)*Diff(p,z);

r = a, v(a) = 0; r = b, v(b) = u;

117

2.Внешний цилиндр неподвижен:

>Diff(Diff(v[z],r),r)+(1/r)*Diff(v[z],r)

=(1/mu)*Diff(p,z);

r = a, v(a) = w; r = b, v(b) = 0;

Перейдем к безразмерным величинам

> r = xi*a, z = e*l0, p = (p-p1)/(p0-p1);

Для скорости мы не можем указать безразмерную величину. В этом случае в качестве нормирующей величины можно выбрать такую комбинацию известных данных, чтобы она совпадала по размерности с размерностью скорости. Обозначим эту безразмерную величину через v0.

>(v0/a^2)*(Diff(Diff(V,xi),xi)+(1/xi)*Diff(V,xi))

=((p0-p1)/(mu*l0))*Diff(p,e);

Безразмерная скорость может быть введена по правилу

>V = v/(((p0-p1)*a^2)/(l0*mu));

Вновых безразмерных переменных для функции p(e) получаем уравнение

>Diff(Diff(p,e),e) = 0;

Для функции V (ξ) уравнение имеет вид

> Diff(Diff(V,xi),xi)+(1/xi)*Diff(V,xi) = Diff(p,e);

Введем граничные условия:

1. Внутренний цилиндр неподвижен:

> p(e) = c1*e+c2;

Подставим граничные условия

> с1 = -1, с2 = 1;

Окончательное выражение для распределения безразмерного давления имеет вид

118

>p(e) = 1-e; Diff(Diff(V,xi),xi)+(1/xi)*Diff(v,xi) = -1; (1/xi)*Diff((xi*Diff(V,xi)),xi) = -1; Diff((xi*Diff(V,xi)),xi) = -xi; xi*Diff(V,xi) = -1/2*xi^2+c3;

Diff(V,xi) = -1/2*xi+c3/xi; V(xi) = -1/4*xi^2+c3*ln(xi)+c4;

Подставим граничные условия

> c3 = (b^2+3*a^2)/(4*a^2*ln(b/a)), c4 = 1/4;

Окончательное выражение для безразмерной скорости течения жидкости имеет вид

>V(xi) = -1/4*xi^2+(b^2+3*a^2) /(4*a^2*ln(b/a))*ln(xi)+1/4;

2.Внешний цилиндр неподвижен:

>p(e) = c1*e+c2;

Подставим граничные условия

> с1 = -1, с2 = 1;

Окончательное выражение для распределения безразмерного давления имеет вид

>p(e) = 1-e;

>Diff(Diff(V,xi),xi)+(1/xi)*Diff(v,xi) = -1; (1/xi)*Diff((xi*Diff(V,xi)),xi) = -1; Diff((xi*Diff(V,xi)),xi) = -xi; xi*Diff(V,xi) = -1/2*xi^2+c3;

Diff(V,xi) = -1/2*xi+c3/xi; V(xi) = -1/4*xi^2+c3*ln(xi)+c4;

Подставим граничные условия

> c3 = (b+5*a)/(4*a*ln(b/a)), c4 = 5/4;

Окончательное выражение для безразмерной скорости течения жидкости имеет вид

> V(xi) = -1/4*xi^2+(b+5*a)/(4*a*ln(b/a))*ln(xi)+5/4;

119

Вычисление основных характеристик потока

Распределение скорости течения жидкости определяется выражением, получаемым после перехода от безразмерной функции V (ξ) к размерной v(r) .

1.Внутренний цилиндр неподвижен:

>v(r) = (1/4*mu)*(-Diff(p,z)) *(((b^2+3*a^2)*ln(r/a))/ln(b/a)+a^2-r^2);

2.Внешний цилиндр неподвижен:

>v(r) = (1/4*mu)*(-Diff(p,z)) *(5*a^2+((a*b+5*a^2)*ln(r/a))/ln(b/a)-r^2);

Анализ полученного решения

1. Внутренний цилиндр неподвижен:

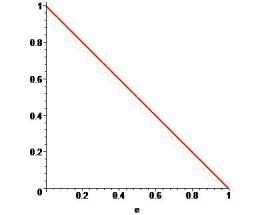
Функция p(e) линейно убывает на отрезке [0, 1] , принимая на его концах значения, равные соответственно 1 и 0 . Функция является монотонно убывающей с постоянным углом наклона, равным −1.

>p := e -> 1-e; plot(p(e), e=0..1);

>b := 6; a := 3;

>V := xi -> -1/4*xi^2+(b^2+3*a^2)

/(4*a^2*ln(b/a))*ln(xi)+1/4; plot(V(xi), xi=1..b/a);

120