
- •Элементы векторной алгебры
- •Содержание
- •1. Векторы § 1 Векторы. Операции над векторами. Проекция вектора на ось
- •1.1. Основные понятия
- •1.2. Линейные операции над векторами
- •1.3. Свойства линейных операций над векторами
- •1.4. Проекция вектора на ось
- •1.5. Проекции вектора на оси координат
- •1.6: Направляющие косинусы вектора
- •§2 . Разложение вектора по базису
- •§ 3. Скалярное произведение векторов
- •3.1: Определение скалярного произведения векторов
- •3.2: Свойства скалярного произведения векторов
- •3.3. Выражение скалярного произведения через координаты векторов
- •3.4. Деление отрезка в данном отношении
- •§4 . Векторное произведение
- •4.1: Определение векторного произведения
- •4.2. Основные свойства векторного произведения
- •4.3. Выражение векторного произведения через координаты векторов
- •§ 5. Смешанное произведение векторов
- •5.1: Определение и геометрический смысл смешанного произведения
- •5.2. Свойства смешанного произведения.
- •5.3. Выражение смешанного произведения через координаты векторов
- •§6. Аксиоматические построения и система аксиом
- •6.1. Векторное пространство, n - мерный вектор
- •6.2. Векторы в экономике
- •§ 7. Решение типовых задач
- •1). Действия над векторами
- •2). Скалярное произведение векторов
- •3) Векторное произведение векторов
- •3) Смешанное произведение векторов
- •Определение объемов параллелепипеда и треугольной пирамиды
- •Определение взаимной ориентации векторов
- •2. Задачи для самостоятельной работы
- •3. Ответы:
- •5. Контрольная работа
- •6. Библиографический список
5.3. Выражение смешанного произведения через координаты векторов
Теорема:
Если векторы
![]() ,
,![]() ,
,
![]() заданы своими координатами
заданы своими координатами![]() =Х1
У1
Z1
и
=Х1
У1
Z1
и
![]() =Х2У2
Z2
,
=Х2У2
Z2
,![]() ={Х3;
У3;
Z3},
то смешанное произведение
={Х3;
У3;
Z3},
то смешанное произведение
![]() ·
·![]() ·
·![]() определяется
формулой
определяется
формулой
![]() ·
·
![]() ·
·![]() =
= =Х1
=Х1
 +У1
+У1 +Z1
+Z1
 .
.
Доказательство:
Имеем:![]() ·
·![]() ·
·![]() =
=
![]() · (
· (![]()
![]() ) . По теореме о выражении векторного
произведения через координаты векторов
) . По теореме о выражении векторного
произведения через координаты векторов![]()
![]() =
= ;
; ;
;
![]() .
.
Умножая
скалярно вектор
![]() =Х1У1
Z1
на вектор
=Х1У1
Z1
на вектор
![]()
![]() и используя теорему о выражении
скалярного произведения через координаты
получаем
и используя теорему о выражении
скалярного произведения через координаты
получаем
![]() ·
·
![]() ·
·![]() =
Х1
=
Х1
 + У1
+ У1
 +Z1
+Z1
 .
.
Пример. В пространстве даны четыре точки: А(1; 1; 1), В(4; 4; 4), С (3; 5 ; 5 ), D(2; 4; 7). Найти объем пирамиды, с вершинами в данных точках.
Решение.
Как известно из элементарной геометрии,
объем тетраэдра АВСD
равен одной шестой объема параллелепипеда,
построеного на векторах
![]() ,
,
![]() ,
,
![]() ;
отсюда из теоремы о смешанном произведении
заключаем, что объем тетраэдра равен
;
отсюда из теоремы о смешанном произведении
заключаем, что объем тетраэдра равен
![]() абсолютной величины смешанного
произведния
абсолютной величины смешанного
произведния
![]() ·
·
![]() ·
·
![]() .
Найдем это смешанное произведение.
Прежде всего, определим координаты
векторов
.
Найдем это смешанное произведение.
Прежде всего, определим координаты
векторов
![]() ;
;
![]() ;
;
![]() .
Для этого из координат конца вектора
вычесть координаты начала:
.
Для этого из координат конца вектора
вычесть координаты начала:
![]() =
{3; 3; 3},
=
{3; 3; 3},
![]() ={2; 4; 4},
={2; 4; 4},
![]() = {1; 3; 6}. Используя теорему о смешанном
произведении, получаем
= {1; 3; 6}. Используя теорему о смешанном
произведении, получаем
![]() ·
·
![]() ·
·
![]() = 3
= 3
![]() + 3
+ 3
![]() + 3
+ 3
![]() = 3 · 12 – 3 · 8 + 3 · 2 = 18. Отсюда V
=
= 3 · 12 – 3 · 8 + 3 · 2 = 18. Отсюда V
=
![]() · 18 = 3 куб. ед.
· 18 = 3 куб. ед.
§6. Аксиоматические построения и система аксиом
6.1. Векторное пространство, n - мерный вектор
Множество
всех плоских или пространственных
векторов, рассмотренных ранее нами, в
которых определены операции сложения
векторов и умножения вектора на число,
являются простейшими примерами векторных
пространств, в частности
![]() = {Х; У;Z}
– вектор в трехмерном пространстве.
Очень часто при вычислениях, связанных
с векторами отвлекаешься от геометрического
смысла вектора и имеешь дело лишь с его
координатами. По аналогии с описанной
моделью множества векторов трехмерного
пространства можно рассмотреть понятие
n
- мерного векторного пространства.
= {Х; У;Z}
– вектор в трехмерном пространстве.
Очень часто при вычислениях, связанных
с векторами отвлекаешься от геометрического
смысла вектора и имеешь дело лишь с его
координатами. По аналогии с описанной
моделью множества векторов трехмерного
пространства можно рассмотреть понятие
n
- мерного векторного пространства.
Определение:
n
– мерным вектором называется упорядоченная
совокупность n
действительных чисел, записываемых в
виде
![]() =
( х1,
х2,
х3,
....., х n
)
=
( х1,
х2,
х3,
....., х n
)
Понятие
n
– мерного вектора широко используется
в экономике, например, некоторый набор
товаров можно охарактеризовать вектором
![]() =
(х1,
х2,
х3,
....., х n
), а соответствующие цены – вектором
=
(х1,
х2,
х3,
....., х n
), а соответствующие цены – вектором
![]() =
( у1,
у2 ,у
3,....уn
).
=
( у1,
у2 ,у
3,....уn
).
Два
n
– мерных вектора равны тогда и только
тогда, когда равны их соответствующие
компоненты, т. е.
![]() =
=
![]() ,
если хi
=уi,
i
= 1,2,3.....,n.
,
если хi
=уi,
i
= 1,2,3.....,n.
Суммой
двух векторов одинаковой размерности
n
называется вектор
![]() =
=
![]() +
+
![]() ,
компоненты которого равны сумме
соответствующих компонент слагаемых
векторов, т. е . zi
= хi
+ уi
i
= 1,2,3....., n.
,
компоненты которого равны сумме
соответствующих компонент слагаемых
векторов, т. е . zi
= хi
+ уi
i
= 1,2,3....., n.
Произведением
вектора
![]() на действительное число
называется вектор
на действительное число
называется вектор
![]() =
=
![]() ,
компонентыui
которого равны произведению
на соответствующие компоненты вектора
,
компонентыui
которого равны произведению
на соответствующие компоненты вектора
![]() ,
т. е.ui
=
х i
, i
= 1, 2, 3....., n.
,
т. е.ui
=
х i
, i
= 1, 2, 3....., n.
Линейные операции над любыми векторами удовлетворяют следующими свойствами:
 +
+
 =
=
 +
+
 - коммутативное (переместительное)
свойство суммы.
- коммутативное (переместительное)
свойство суммы.(
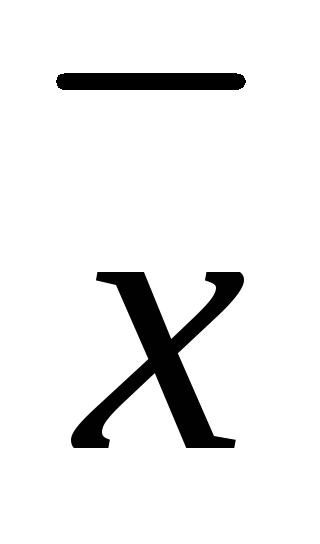 +
+
 )
+
)
+
 =
=
 + (
+ ( +
+
 )
– ассоциативное (сочетательное) свойство
суммы.
)
– ассоциативное (сочетательное) свойство
суммы.(
 ) = (
)
) = (
)
 - ассоциативное относительно числового
множителя свойство.
- ассоциативное относительно числового
множителя свойство.( + )
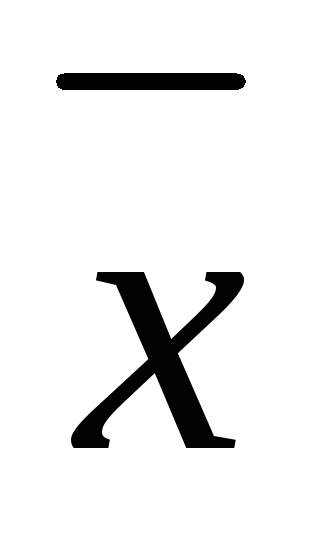 =
=
 +
+
 – дистрибутивное (распределительное)
относительно суммы числовых множителей
свойство.
– дистрибутивное (распределительное)
относительно суммы числовых множителей
свойство.(
 +
+
 )
=
)
=
 +
+
 –
дистрибутивное относительно суммы
векторов свойство.
–
дистрибутивное относительно суммы
векторов свойство.Существует нулевой вектор
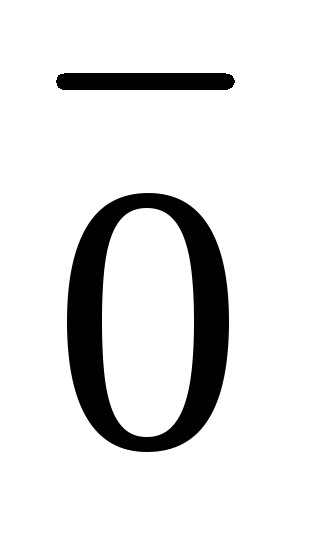 =(0
, 0,.....0) такой, что
=(0
, 0,.....0) такой, что
 +
+
 =
=
 для любого вектора
для любого вектора (особая роль нулевого вектора ).
(особая роль нулевого вектора ).Для любого вектора
 существует противоположный вектор (-
существует противоположный вектор (- )
такой, что
)
такой, что +( -
+( - ) =
) =
 .
.1
 =
= для любого вектора
для любого вектора (особая роль числового множителя 1).
(особая роль числового множителя 1).
Определение: Множество векторов с действительными компонентами, в котором определены операции сложения векторов и умножения вектора на число, удовлетворяющее приведенным выше восьми свойствам (рассматриваемым как аксиомы), называется векторным пространством.
По аналогии с линейно зависимыми и линейно независимыми строками матрицы вводится понятие линейной независимости векторов.
Определение:
Вектор
![]() m
называется
линейно комбинацией векторов
m
называется
линейно комбинацией векторов
![]() 1,
1,
![]() 2,
2,
![]() 3,....
3,....
![]() m
векторного
пространства R,
если он равен сумме произведений этих
векторов на произвольные действительные
числа:
m
векторного
пространства R,
если он равен сумме произведений этих
векторов на произвольные действительные
числа:
![]() m
= 1
m
= 1
![]() 1+
2
1+
2
![]() 2+
3
2+
3
![]() 3+....+
m-1
3+....+
m-1
![]() m-1
, где 1
, 2
, ...
m-1-
произвольные действительные числа.
m-1
, где 1
, 2
, ...
m-1-
произвольные действительные числа.
Определение:
Векторы
![]() 1,
1,
![]() 2,
2,
![]() 3,....
3,....
![]() m
векторного
пространства R
называются линейно зависимыми, если
существуют такие числа 1
, 2
, .....
m
, не равные
одновременно нулю, что
m
векторного
пространства R
называются линейно зависимыми, если
существуют такие числа 1
, 2
, .....
m
, не равные
одновременно нулю, что
1
![]() 1
+ 2
1
+ 2![]() 2+
... +.
m
2+
... +.
m![]() m=
m=
![]() .
.
В
противном случае векторы
![]() 1,
1,
![]() 2,
2,
![]() 3,....
3,....
![]() m
называются
линейно независимыми.
m
называются
линейно независимыми.
Если
векторы
![]() 1,
1,
![]() 2,
2,
![]() 3,....
3,....
![]() m
линейно зависимы, то, по крайней мере,
один из них линейно выражается через
остальные. Верно и обратное утверждение
о том, что если один из векторов выражается
линейно через остальные, то все эти
векторы в совокупности линейно зависимы.
m
линейно зависимы, то, по крайней мере,
один из них линейно выражается через
остальные. Верно и обратное утверждение
о том, что если один из векторов выражается
линейно через остальные, то все эти
векторы в совокупности линейно зависимы.
Примером
линейно независимых векторов являются
два неколлинеарных вектора
![]() 1
и
1
и
![]() 2
на плоскости. Действительно, условие
1
2
на плоскости. Действительно, условие
1
![]() 1+
2
1+
2
![]() 2
= 0 будет выполняться лишь в случае,
когда
2
= 0 будет выполняться лишь в случае,
когда
1=
2
= 0, ибо если, например 2
0, то
![]() 2
= –
2
= –
![]()
![]() 1
и векторы
1
и векторы
![]() 1
и
1
и
![]() 2
коллинеарны.
Однако любые три вектора плоскости
линейно зависимы.
2
коллинеарны.
Однако любые три вектора плоскости
линейно зависимы.
Свойства векторов линейного пространства:
Если среди векторов
 1,
1,
 2,
2,
 3,....
3,....
 m
имеется
нулевой, то эти векторы линейно зависимы.
m
имеется
нулевой, то эти векторы линейно зависимы.
Если часть векторов
 1,
1,
 2,
2,
 3,....
3,....
 m
являются линейно зависимыми, то и все
эти векторы – линейно зависимые.
m
являются линейно зависимыми, то и все
эти векторы – линейно зависимые.
Действительно,
если, например, векторы
![]() 1,
1,
![]() 2,
2,
![]() 3,....
3,....
![]() m
линейно
зависимы, то справедливо равенство
2
m
линейно
зависимы, то справедливо равенство
2
![]() 2
+
m
2
+
m![]() m=
m=
![]() ,
в котором не все числа 2....
m
и 1=
0 будет справедливо равенство 1
,
в котором не все числа 2....
m
и 1=
0 будет справедливо равенство 1
![]() 1
+ 2
1
+ 2
![]() 2+
... +.
m
2+
... +.
m![]() m=
m=
![]() .
.
Пример:
Выяснить, являются ли векторы
![]() 1
=(1, 3, 1, 3),
1
=(1, 3, 1, 3),
![]() 2
= (2, 1, 1, 2 ),
2
= (2, 1, 1, 2 ),
![]() 3
= ( 3, - 1, 1, 1 ) линейно зависимыми.
3
= ( 3, - 1, 1, 1 ) линейно зависимыми.
Решение.
Составим векторное равенство 1
![]() 1
+ 2
1
+ 2
![]() 2+3
2+3
![]() 3
=
3
=
![]() или
или
1
![]() + 2
+ 2
![]() + 3
+ 3
![]() =
=
![]() .
.
Задача свелась, таким образом, к решению системы:
 Решая
систему методом Гаусса, приведем ее к
виду:
Решая
систему методом Гаусса, приведем ее к
виду:
 откуда
найдем бесконечное множество ее решений
(1
= с, 2
= -2с, 3
= с), где с
- произвольное действительное число.
откуда
найдем бесконечное множество ее решений
(1
= с, 2
= -2с, 3
= с), где с
- произвольное действительное число.
Итак,
для данных векторов условие 1
![]() 1
+ 2
1
+ 2![]() 2+
... +.
m
2+
... +.
m![]() m=
m=
![]() выполняется не толдько при 1
= 2
= 3
=0 (а, например,
при 1=1,
2
= -2, 3
=1 (с =1); при
1
=2, 2
=-4, 3
=2 (с =2) и
т.д.), следовательно, эти векторы –
линейно зависимые.
выполняется не толдько при 1
= 2
= 3
=0 (а, например,
при 1=1,
2
= -2, 3
=1 (с =1); при
1
=2, 2
=-4, 3
=2 (с =2) и
т.д.), следовательно, эти векторы –
линейно зависимые.
Линейное пространство R называется n- мерным, если в нем существует n линейно независимым вектором, а любые из (n + 1) векторов уже являются зависимыми. Другими словами, размерность пространства - это максимальное число содержащихся в нем линейно независимых векторов. Число n называется размерностью пространства R и обозначает dim(R) .
Совокупность n линейно независимых векторов n- мерного пространства R называется базисом.
Теорема: Каждый вектор х линейного пространства R можно представить и притом единственным способом в виде линейной комбинации векторов базиса.
Доказательство:
Пусть векторы е1, е2 ,..., еn образуют произвольный базис n- мерного пространства R . Так как любые из
(n + 1) векторов n- мерного пространства R зависимы , то будут зависимы , в частности , векторы е1 , е2,..., еn и рассматриваемый вектор х. Тогда существуют такие не равные одновременно нулю числа 1, 2 ,n , , что
1 е1 + 2 е2 +...+ n е n + х =0
При этом 0, ибо в противном случае , если = 0 и хотя бы одно из чисел 1, 2 ,..., n было бы
отлично от нуля, то векторы е1 , е2 ,..., еn были бы линейно зависимы. Следовательно,
![]() =
-
=
-
![]() е1
-
е1
-
![]() е2
- ... -
е2
- ... -
![]() е n
или
е n
или
![]() =
х1
е1
+ х2
е2
+...+х
n
е n
где х i
= -
=
х1
е1
+ х2
е2
+...+х
n
е n
где х i
= -
![]() (i
= 1, 2, ...., n)
(*)
(i
= 1, 2, ...., n)
(*)
Это
выражение
![]() через е1,
е2,...,
е n
единственное, так как если допустить
какое – либо другое выражение, например,
через е1,
е2,...,
е n
единственное, так как если допустить
какое – либо другое выражение, например,
![]() =
у1
е1
+ у2
е2
+...+у
n
е n
, то, вычитая
из него почленно (
), получим
=
у1
е1
+ у2
е2
+...+у
n
е n
, то, вычитая
из него почленно (
), получим
( у1 – х 1) е1 + (у2 – х 2) е2 + ...+ (у n – х n) е n = 0 , откуда из условия линейной независимости векторов е1 , е2,..., е n следует, что у1 – х 1= у2 – х 2= ...= у n – х n = 0 или у1 = х 1, у2 = х 2 ... у n = х n у n = х n .
Равенство
(
) называется разложением вектора
![]() по базису е1
, е2,...,
е n,
а числа х 1,
х 2
... х n
– координаты вектора
по базису е1
, е2,...,
е n,
а числа х 1,
х 2
... х n
– координаты вектора
![]() относительно этого базиса. В силу
единственности этого разложения каждый
вектор однозначно может быть определен
координатами в некотором базисе.
относительно этого базиса. В силу
единственности этого разложения каждый
вектор однозначно может быть определен
координатами в некотором базисе.
Важное значение имеет следующая теорема, которую мы приведем без доказательства:
Теорема. Если е1 , е2,..., е n – система линейно независимых векторов пространства R и любой вектор а линейно выражается через е1 , е2,..., е n ,то пространство R является n- мерным , а векторы е1 , е2,..., е n – его базисом.
Пример. В базисе е1, е2 , е3 заданы векторы а1 = (1; 1; 0), а2 = (1; -1; 1) и а3 = (-3; 5;-6) . Показать, что векторы а1 ,а2 , а3 образуют базис.
Решение. Векторы а1 , а2 , а3 образуют базис, если они линейно независимы. Составим векторное равенство: 1 а1+ 2 а2 + 3 а 3 = 0. Решая его аналогично примеру 1 можно убедиться в единственном нулевом решении: 1 + 2 + 3 = 0 , т.е. векторы а1 , а2 , а3 образуют систему линейно независимых векторов и, следовательно, составляют базис.
