
- •Элементы векторной алгебры
- •Содержание
- •1. Векторы § 1 Векторы. Операции над векторами. Проекция вектора на ось
- •1.1. Основные понятия
- •1.2. Линейные операции над векторами
- •1.3. Свойства линейных операций над векторами
- •1.4. Проекция вектора на ось
- •1.5. Проекции вектора на оси координат
- •1.6: Направляющие косинусы вектора
- •§2 . Разложение вектора по базису
- •§ 3. Скалярное произведение векторов
- •3.1: Определение скалярного произведения векторов
- •3.2: Свойства скалярного произведения векторов
- •3.3. Выражение скалярного произведения через координаты векторов
- •3.4. Деление отрезка в данном отношении
- •§4 . Векторное произведение
- •4.1: Определение векторного произведения
- •4.2. Основные свойства векторного произведения
- •4.3. Выражение векторного произведения через координаты векторов
- •§ 5. Смешанное произведение векторов
- •5.1: Определение и геометрический смысл смешанного произведения
- •5.2. Свойства смешанного произведения.
- •5.3. Выражение смешанного произведения через координаты векторов
- •§6. Аксиоматические построения и система аксиом
- •6.1. Векторное пространство, n - мерный вектор
- •6.2. Векторы в экономике
- •§ 7. Решение типовых задач
- •1). Действия над векторами
- •2). Скалярное произведение векторов
- •3) Векторное произведение векторов
- •3) Смешанное произведение векторов
- •Определение объемов параллелепипеда и треугольной пирамиды
- •Определение взаимной ориентации векторов
- •2. Задачи для самостоятельной работы
- •3. Ответы:
- •5. Контрольная работа
- •6. Библиографический список
§ 7. Решение типовых задач
1). Действия над векторами
Линейные операции над векторами:
При сложении, вычитании, умножении вектора на число их одноименные координаты складываются, вычитаются, умножаются на число
Пример
1:
![]() Найти
Найти
![]()
Решение:
![]() =2
=2![]() =
(4; 14; -6) + (2;-2;-1)=(6; 12;-7)
=
(4; 14; -6) + (2;-2;-1)=(6; 12;-7)
Равенство векторов
Равные векторы имеют и равные одноименные координаты:
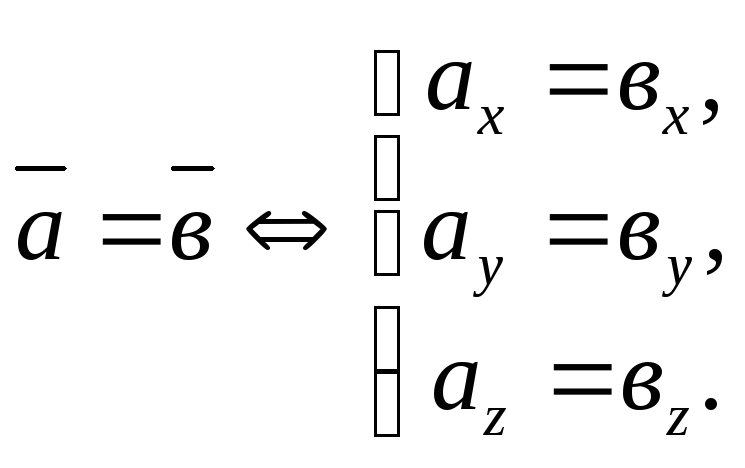
Коллинеарность векторов
Одноименные
координаты коллинеарных векторов
пропорциональны:
![]() ║
║![]() .
.
2). Скалярное произведение векторов
Угол между векторами
Пример
2: Векторы
![]() и
и
![]() образуют угол
=
образуют угол
=
![]() Найти длину вектора
Найти длину вектора
![]() = 2
= 2
![]() - 3
- 3
![]() ,
если
,
если
![]() = 2,
= 2,
![]() = 1.
= 1.
Решение.
Согласно
свойству скалярного проиведения, квадрат
длины вектора
![]() равен его скалярному квадрату. Найдем
скалярный квадрат вектора
равен его скалярному квадрату. Найдем
скалярный квадрат вектора
![]() :
:
![]() =
4
=
4
![]() - 12
- 12![]()
![]() + 9
+ 9
![]() =
4
=
4
![]() - 12
- 12
![]()
![]() cos
+ 9
cos
+ 9
![]() = 4 * 2 2
– 12 * 2 * 1 cos
(
= 4 * 2 2
– 12 * 2 * 1 cos
(![]() )
+ 9 * 12
= 16 –12+ + 9 = 13. Следовательно,
)
+ 9 * 12
= 16 –12+ + 9 = 13. Следовательно,
![]() =
=![]()
Пример 3: Найти угол А в треугольнике с вершинами А (1; 2; - 1), В (5; 5; 11), С (13; 18; 20).
Решение.
Искомый угол – это угол между векторами
![]() =
=
![]() =
{4;3;12} и
=
{4;3;12} и
![]() =
=
![]() = {12;16;21}. По формуле (§3, следствие 2 ) имеем:
= {12;16;21}. По формуле (§3, следствие 2 ) имеем:
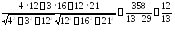
Cos А =
Таким
образом, угол А
= arccos
(![]() )
23 0
.
)
23 0
.
Пример
4: Даны вершины
треугольника: А(2;-1;3), В(1;1;1), С(0;0;5). Найдите
длину стороны АВ и
![]() .
.
Решение: Найдем координаты вектора, зная координаты его начала и конца:
![]()
![]() ,
,
![]() .
. ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
Ответ:
![]() ,
,![]() .
.
Пример
5:
![]() Найти
Найти
![]()
Решение. Воспользуемся формулой

где
![]() – скалярное произведение векторов
– скалярное произведение векторов
![]() и
и
![]() .
.
Вычислим
![]() :
:
![]()
Найдем модули векторов

Тогда
![]()
Пример 6.
Вектор
![]() ортогонален
вектору
ортогонален
вектору
![]() Найти
Найти
![]()
Решение.
Так
как вектор
![]() ортогонален
вектору
ортогонален
вектору
![]() ,то
,то
![]() ,
и, значит, скалярное произведение этих
векторов тоже равно нулю:
,
и, значит, скалярное произведение этих
векторов тоже равно нулю:
![]()
С другой стороны
![]()
Итак,
![]() и
и
![]()
Проекция вектора на заданное направление
Пример
7: Даны векторы
![]() =
2
- 4
2 ,
=
2
- 4
2 ,
![]() = 0
6 -
2 ,
= 0
6 -
2 ,
![]() = 2
6
5.
Найти проекцию вектора
= 2
6
5.
Найти проекцию вектора
![]() +
+![]() на
на
![]() +
+![]()
Решение.
Найдем координаты векторов
![]() +
+![]() и
и
![]() +
+![]() ,
учитывая, что при сложении векторов их
соответствующие координаты складываются.
Итак,
,
учитывая, что при сложении векторов их
соответствующие координаты складываются.
Итак,
![]() +
+
![]() =
4
2
7,
=
4
2
7,
![]() +
+![]() = 2
12
3.
Теперь по формуле (2) из §3 получаем
= 2
12
3.
Теперь по формуле (2) из §3 получаем
ПР![]()
![]() =
=![]()
![]()
4,23.
4,23.
Пример
8: Найти
![]() ,если
,если
![]()
Решение.
Проекция
вектора
![]() на вектор
на вектор
![]() определяется
по формуле
определяется
по формуле
 .
.
Найдем
координаты вектора
![]() :
:
![]()
Вычислим
скалярное произведение векторов
![]() и
и
![]()
![]()
и
модуль вектора
![]()
![]()
Тогда
![]()
Работа постоянной силы
Пусть
материальная точка перемещается
прямолинейно из положения А в положение
В под действием силы F,
образующей угол α с перемещением АВ
=S.
Из физики
известно, что работа силы F
при перемещении
S
равна
А
= F
![]() S
S
![]() cos
α, т. е. А = F
cos
α, т. е. А = F
![]() S.
S.
Таким образом, работа постоянной силы при прямолинейном перемещении равна скалярному произведению вектора силы на вектор перемещения.
3) Векторное произведение векторов
Нахождение площади параллелограмма и треугольника
Пример 9. Найти площадь треугольника АВС с вершинами А(2 2 2), В(1; 3; 3), С(3; 4; 2 ).
Решение.
Площадь треугольника АВС равна половине
площади параллелограмма, построенного
на векторах
![]() и
и![]() ,
т. е. половине длины векторного произведения
этих векторов. Так как
,
т. е. половине длины векторного произведения
этих векторов. Так как![]() =-1;
1; 1,
=-1;
1; 1,
![]() =1;
2; 0 ,
то
=1;
2; 0 ,
то ![]()
![]() =
=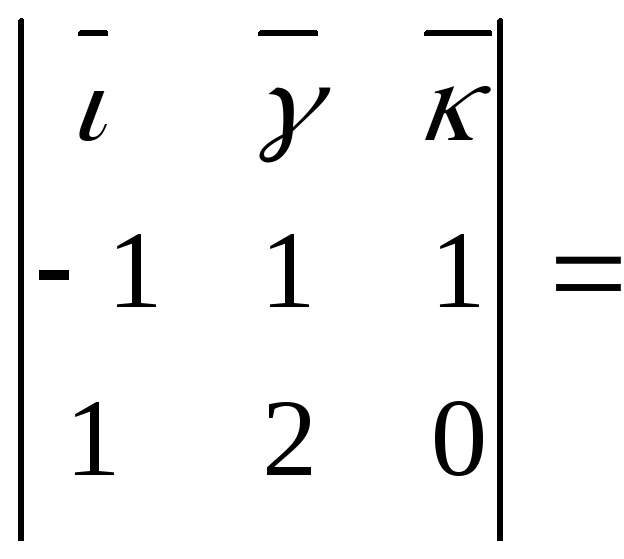 -
2
-
2![]() +
+![]() - 3
- 3![]() .
Отсюда
.
Отсюда
![]() и
S
АВС =
и
S
АВС =
![]()
Пример
10. Найти
площадь треугольника с вершинами в
точках
![]()
![]()
Решение.
Площадь
треугольника, построенного на векторах
![]() и
и![]() ,может быть
найдена по формуле:
,может быть
найдена по формуле:
![]()
где
 векторное
произведение векторов
векторное
произведение векторов
![]() и
и![]() .
.
Примем
![]() ,
,![]() Вычислим координаты векторов
Вычислим координаты векторов![]() и
и![]() :
:
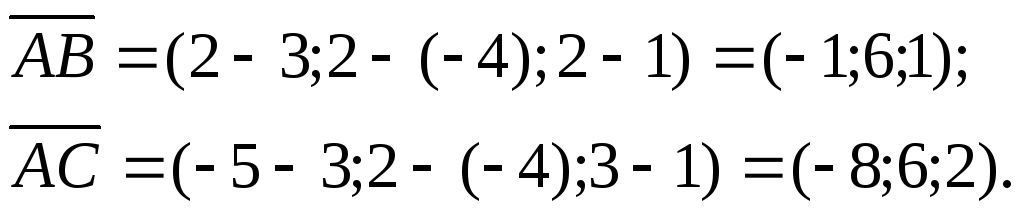
Найдем векторное произведение этих векторов

Тогда
![]()
Следовательно,
![]()
Пример 11:
Известно,
что
![]() а
угол между
а
угол между
![]() и
и![]() равен
равен
![]() Найти
Найти
![]() .
.
Решение.
Согласно
определению векторного произведения
![]() имеет место формула
имеет место формула
![]()
Тогда

Подставив исходные данные, получим

Установление каллинеарности векторов
![]() ║
║![]()
![]()
![]()
![]()
![]() =
=
![]() и наооборот:
и наооборот:![]()
![]()
![]() =
=![]()
![]()
![]() ║
║![]() .
.
Нахождение момента силы относительно точки
Пусть в точке А приложена сила F=АВ и пусть О – некоторая точка пространства. Из физики известно, что моментом силы F относительно точки О называется вектор М, который проходит через точку О и:
перпендикулярен плоскости, проходящей через точки О, А, В;
численно равен произведению силы на плечо;
образует правую тройку векторов.
Стало
быть, М = ОА
![]() F
F
