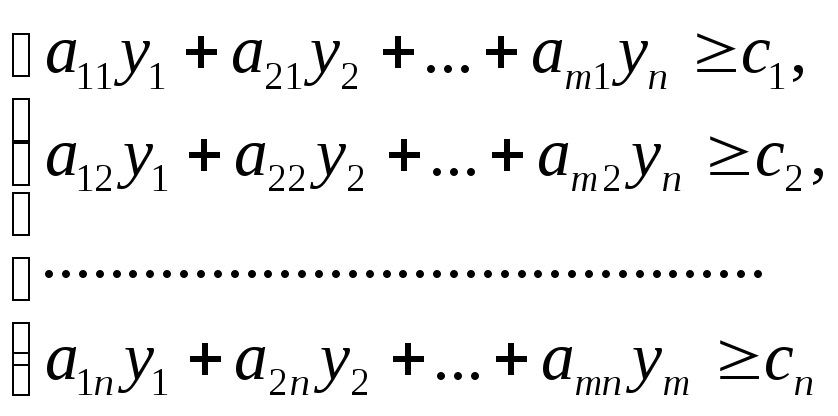Тема 2. Линейное программирование

Задачами линейного программирования(ЛП) называются задачи, в которых линейны как целевая функция, так и ограничения в виде равенств неравенств и для которых методы математического анализа оказываются непригодными. ЛП представляет собой наиболее часто используемый метод оптимизации.

Рассмотрим систему уравнений и неравенств спеременными (неизвестными):

(1)

и линейную функцию:

(2)

Требуется найти решение системы (1) при котором целевая функция принимает оптимальное значение (максимальное или минимальное).

Такая задача называется задачей линейного программирования в общем виде. Система (1) называетсясистемой ограничений (областью допустимых решений). Функция (2) называетсяцелевой функцией.

Оптимальным решением задачи ЛП называется решениесистемы ограничений (2), при котором целевая функция принимает оптимальное значение.

Рассмотрим задачу ЛП в стандартной форме для случая двух переменных :

(9)

(10)

Пусть система неравенств (10) совместна (имеет хотя бы одно решение). Любое неравенство этой системы геометрически определяет полуплоскость с граничной прямой Условия не отрицательности определяют полуплоскости с соответственными граничными прямыми и.

Так как система совместна, то полуплоскости, как выпуклые множества, пересекаясь, образуют общую часть, которая является выпуклым множеством и представляет собой совокупность точек, координаты каждой из которых являются решением данной системы. Совокупность всех этих точек называется многоугольником решений. Это может быть точка, отрезок, луч, прямая, замкнутый многоугольник, неограниченная многоугольная область.

Решение ЗЛП геометрически представляет собой поиск такой точки ногоугольника решений, координаты которой доставляют целевой функции наибольшее (наименьшее) значение. Причем допустимым решением являются все точки многогранника.

Алгоритм решения задачи линейного программирования графическим методом (число переменных ).

1. Строится многоугольная область допустимых решений на плоскости соответствующая ограничениям. Затем строится вектор-градиент

целевой функции zв любой точкеобласть допустимых решений.

2. Прямая(линия уровня функцииz), перпендикулярная вектору-градиенту, передвигается параллельно самой себе в направлении вектора-градиента в случае задачи на максимум (и в противоположном направлении - в случае задачи на минимум) до тех пор, пока она не покинет область допустимых решений. Предельная точка (или точки) области являются оптимальными точками.

3. Для нахождения координат оптимальной точки, надо решить систему уравнений, которая соответствует прямым, пересечение которых образует эту точку. Значение целевой функции в этой точке будет оптимальным, а сами координаты точки будут являться решением задачи ЛП.

Контрольное задание №2.

Решить графически и симплекс-методом задачу линейного программирования:

Тема 3 Двойственные задачи линейного программирования

Две задачи ЛП, обладающие следующими свойствами называются двойственными.

1. В одной задачи ищется максимум, в другой минимум линейной функции.

2. Коэффициенты при переменных в целевой функции одной задачи являются свободными членами системы ограничений другой задачи.

3. Каждая задача записана в стандартной форме, причем в задаче на минимум все неравенства вида «», а в задаче на максимум - вида «».

4. Матрицы коэффициентов при переменных в системах ограничений

обоих задач являются транспонированными друг к другу: и.

5. Число неравенств в системе ограничений одной задачи совпадает с числом переменных другой задачи.

6. Условия неотрицательности переменных имеются в обеих задачах.

Иисходная	Двойственная
Целевая функция:	Целевая функция:
При ограничениях	При ограничениях
и условиях неотрицательности Составить такой план выпуска продукции при котором прибыль от реализации продукции будет максимальной при условии, что потребление ресурсов по каждому виду продукции не превзойдёт имеющихся запасов.	и условиях неотрицательности Найти такой набор цен оценок) ресурсовпри котором общие затраты на ресурсы будут минимальны при условии, что затраты на ресурсы при производстве каждого вида продукции будут не менее прибыли от реализации этой продукции

Первая (основная) теорема двойственности: если одна из взаимно двойственных задач имеет оптимальное решение, то его имеет и другая задача, причем оптимальные значения их целевых функций равны: Если область допустимых решений одной из задач неограниченна, то условия другой задачи противоречивы.

Замечание. Обратное утверждение вообще говоря не верно. Именно: если условия одной задачи противоречивы, это вообще говоря не означает, что другая задача неограниченна.

Вторая теорема двойственности. Компоненты оптимального решения двойственной задачи равны абсолютным значениям коэффициентов при соответствующих переменных целевой функции, выраженной через не основные переменные, ее оптимального решения

Третья теорема двойственности.Компоненты оптимального решения двойственной задачи равны значениям частных производных функции по соответствующим аргументам

Метод, при котором сначала симплекс-методом решается двойственная задача, а затем оптимум и оптимальное решение исходной задачи находится с помощью теорем двойственности, называется двойственным симплекс методом. Он применяется в случаях, когда первое базисное решение недопустимо или при.

Компоненты оптимального решения двойственной задачи называются оптимальными (двойственными или объективно обусловленными) оценками исходной задачи.

Двойственные оценки служат инструментом анализа и принятия правильных решений в условиях постоянно меняющегося производства.