Математические методы в экономике

(ЭММ)

Для студентов экономических факультетов

Заочное отделение

Вопросы для самоконтроля

1. Общая задача линейного программирования.

2. Задача об использовании ресурсов.

З. Задача составления рациона.

4. Задача о раскрое материала.

5. Геометрический метод решения задач линейного программирования.

6. Понятие об игровых моделях.

7. Платежная матрица. Нижняя и верхняя цена игры. Седловая точка.

8. Игра «поиск».

9. Дилемма заключенного. Проблема рекламы.

10.Решение игр в смешанных стратегиях.

11 Геометрическая интерпретация игры 2 х n и m х 2.

12.Системы массового обслуживания (СМО): основные понятия.

13.Граф состояний СМО. Предельные вероятности состояний.

14.Модель Леонтьева многоотраслевой экономики.

Разбор варианта контрольной работы

Задача №1. Определить нижнюю и верхнюю цену игры, заданной платежной матрицей

3 -2 1

P= 1 -1 1

2 0 4

Имеет ли игра седловую точку?

Решение. Найдем по каждой строчке платежной матрицы минимальное число α_i =min(a_i1,a_i2,a_i3) — это гарантированный выигрыш игрока А, при выборе им соответствующей стратегии. Чтобы получить максимально возможный гарантированный выигрыш, игрок А должен выбрать ту стратегию, для которой α_ij имеет максимальное значение­ - α_i =max(a₁,a₂,a₃)— это нижняя цена игры.

Для игрока В выберем по каждому столбцу максимальное число

β_j = max(a_1j,a_2j,a_3j)— это гарантированный проигрыш игрока В при выборе им стратегии β_j. Найдем минимальное из этих чисел β =min(β₁,β₂,β₃)— это верхняя цена игры. Занесем полученные данные в таблицу.

	B1	B2	B3
A1	3	-2	1	α1 =min(3,-2,1)=-2
A2	1	-1	1	α2 =min(1-1,1)=-1
A3	2	0	4	α3 =min(2,0,4)=0
	β1 = max(3,1,2)=3	β2 = max(-2,-1,0)=0	β3 = max(1,1,4)=4	α = max(-2,-1,0) =0 β = min(3,0,4) =0

Нижняя цена игры α =0 равна верхней цене игры β =0. Значит, игра имеет седловую точку. Для игрока А оптимальная стратегия — А₃, для игрока В оптимальная стратегия — В₂.

Ответ: α = β = 0, игра имеет седловую точку, оптимальные стратегии (А₃, В₂).

Задача 2. Решить графически игру, заданную платежной матрицей

Решение. Дана игра 4 х 2, то есть у игрока А имеется 4 стратегии, а у игрока В — 2. Поэтому, будем решать игру для игрока В. Построим оси: ОХ — на ней будем отмечать вероятности, с которыми игрок использует ту или иную стратегии, и ОУ — на ней будем откладывать цену игры. На расстоянии единица от оси ОУ проведем еще ось параллельную ей (см. рис. 1). Если игрок А

выбирает стратегию А₁, то игрок В, используя свои стратегии с вероятностями (q₁,q₂), будет проигрывать, в среднем, q₁•а₁₁ +q₂• а₁₂ = q₁ (-4)+ q₂•0.

Отметим на оси ОУ а₁₁ = -4, а на оси ей параллельной а₁₂ = 0 и соединим эти точки прямой линией она показывает, сколько, в среднем, получает игрок В, если А использует стратегию А₁, а В чередует стратегии В₁ и В₂ с некоторыми вероятностями (q₁,q₂). Аналогично отмечаем на оси ОУ точку —2, а на параллельной ей оси — точку 0 и соединяем отрезком.

Получаем линию, показывающую, сколько , в среднем, получает игрок В, если А выбрал стратегию А₂. Точно также для А₃ и А₄. для игрока В надо выбрать

верхнюю границу, так как он должен рассчитывать, что А выберет ту стратегию, которая соответствует наибольшему проигрышу для игрока В. На рис. 1 это ломанная А₃КА₄, выделенная толстой линией. Игроку В следует выбрать ту смешанную стратегию, которая соответствует наименьшему проигрышу для В

— точка К. Это точка пересечения прямых, соответствующих стратегиям А₃ и А₄. Выпишем уравнения этих прямых.

Прямая (А₃ А₃), проходит через точки с координатами (0; 5) и (1; -2). Уравнение этой прямой запишется в следующем виде:

х—0 у—5 1 5

= <=>x = - y +

1—0 -2-5 7 7

Уравнение прямой (А₄ А₄), проходящей через точки (0; -3) и (1; 3), запишется в следующем виде:

х—0 y-(-3) 1 1

= <=>x = - y +

1—0 3-(-3) 6 2

Точка К — точка пересечения этих прямых, имеет координаты, удовлетворяющие системе:

Решаем систему:

Откуда,

Следовательно, цена игры оптимальная стратегия для игрока В:

Для игрока А, стратегии А₁ и А₂ будут не активными, игроку А не выгодно их использовать. Максимально возможный выигрыш, равный цене игры

игрок А будет получать, используя стратегии А₃ и А₄. Найдем опти-

мальную смешанную стратегию для игрока А из следующей системы, учитывая, что А₁ и А₂ не активные стратегии, то есть p₁ = p₂ = 0:

Ответ: Цена игры оптимальные стратегии игроков

Замечание. Если игра размера 2 x n, то ее следует решать для игрока А. Тогда на чертеже следует выбирать нижнюю границу и максимальное значении этой границы.

Задача №3. Решить геометрически следующую задачу линейного программирования:

Решение. Построим область ограничений. Строим прямую x1 —х2 = —3 по двум точкам, координаты которых удовлетворяют уравнению: (-3; 0), (0, 3) (см. рис. 2). Проверяем, какая полуплоскость удовлетворяет неравенству

x1 —х2 = ≥ -3. Для этого выберем произвольную точку и проверим удовлетворяют ли ее координаты данному неравенству: 0 — 0 ≥ -3. Неравенство верное,

значит, точка с координатами (О, О) лежит в нужной полуплоскости. Рисуем

((бороду» по направлению к этой точке. Аналогично находим полуплоскости, соответствующие оставшимся неравенствам. Пересечение получившихся плоскостей (область, окруженная «бородами») является искомым ограничением. На рис. 2 это пятиугольник, закрашенный серым цветом.

Определим наклон уровней целевой 7 функции. для этого нарисуем прямую для 2 конкретного значения целевой функции. Например, для Р=2 уравнение целевой функции: F = 2 = 2х₁ — 2х₂. Прямая проходит через точки (—1; 0) и (0; 1). Стрелка показывает направление уменьшения значения F. Оптимальное (наименьшее значение целевая функция примет «на выходе» из области ограничения. Так как линии уровня целевой функции параллельны прямой (1), то оптимальное значение целевая функция будет принимать на отрезке, а не в одной точке. Точки этого отрезка задаются уравнением

Задача №4. Имеется два вида корма, содержащие витамины В₁, В₆, В₁₂. Все данные представлены в таблице

Стоимость 1 кг корма I и II соответственно равна б и 8 рублей. Необходимо составить дневной рацион, имеющий минимальную стоимость, в котором содержание вида витаминов было бы не менее установленного предела.

Решение. Составим экономико-математическую модель задачи.

Обозначим х₁, х₂ — количество корма I и II, входящих в дневной рацион.

Тогда этот рацион будет включать (2 х₁+ 1 х₂) единиц витамина В₁,

(2 х₁ +4• х₂) единиц витамина В₆ и (2. х₁ + 2 х₂) единиц витамина В₁₂. Так

как содержание витаминов в рационе должно быть не ниже установленного

предела, то получим систему неравенств:

Кроме того, х₁ ≥0,х₂ ≥0. Общая стоимость рациона питания составит (в руб.):

Итак, наша задача свелась к следующей задаче линейного программирования:

при ограничениях:

Решаем ее геометрическим способом, аналогично задаче №3 (см. рис.3).

Получаем, что оптимальная точка пересечения прямых (2) и (3). Найдем ее координаты и значение целевой функции в ней:

Ответ: Оптимальный рацион 4 кг первого корма и 1 кг — второго, который стоит 32 рубля.

Задача №5. Построить граф состояний следующего случайного процесса: система состоит из лампы и нагревателя. В любой момент времени каждый из приборов может быть выключен или включен. Нагреватель может быть сломан, а лампа не ломается. Кроме того, нагреватель нельзя включить, если не работает лампа.

Р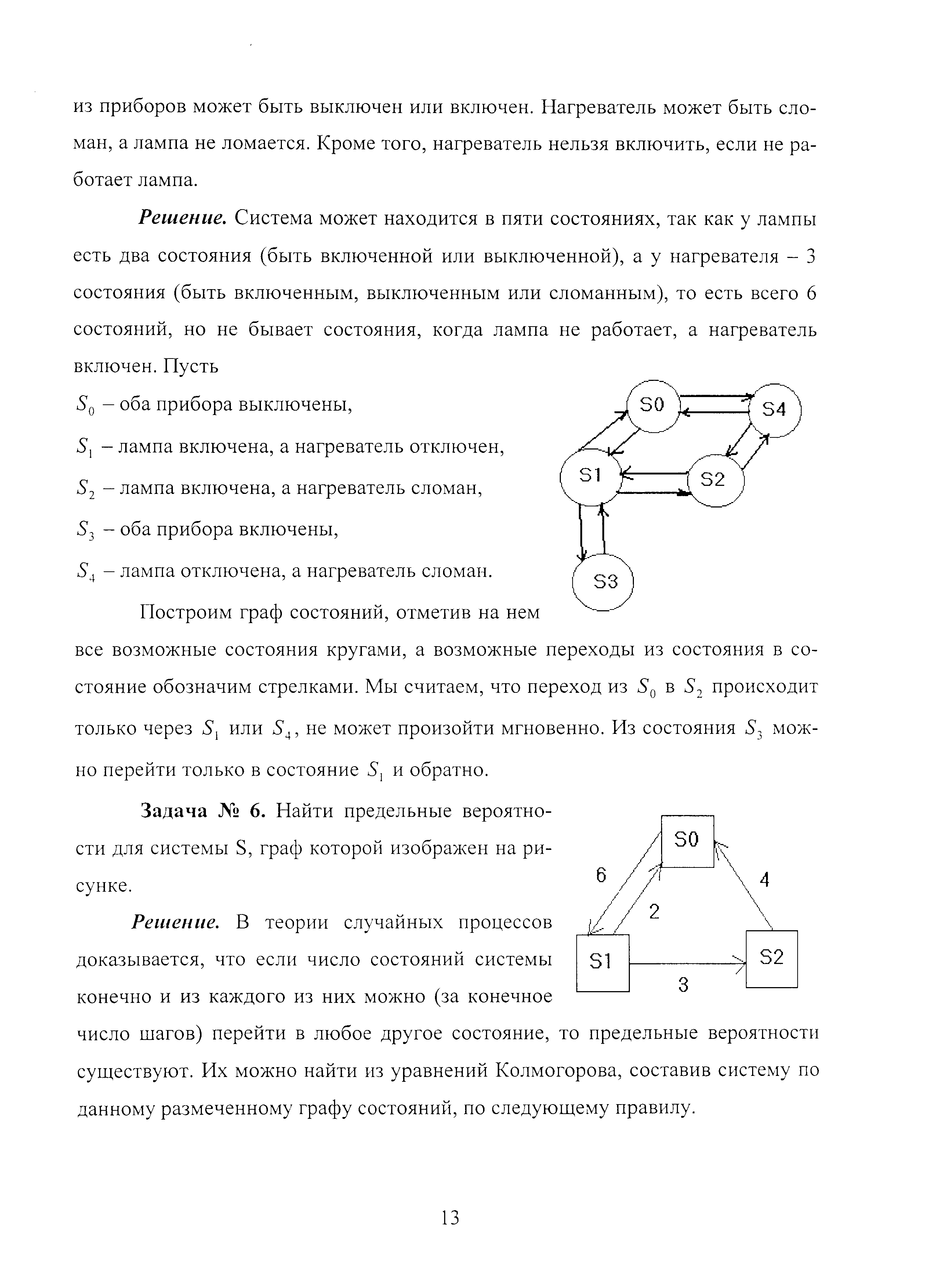ешение. Система может находится в пяти состояниях, так как у лампы есть два состояния (быть включенной или выключенной), а у нагревателя — З состояния (быть включенным, выключенным или сломанным), то есть всего б состояний, но не бывает состояния, когда лампа не работает, а нагреватель включен. Пусть

S₀ — оба прибора выключены,

S₁ — лампа включена, а нагреватель отключен,

S₂ — лампа включена, а нагреватель сломан,

S₃ — оба прибора включены,

S₄ — лампа отключена, а нагреватель сломан.

Построим граф состояний, отметив на нем

все возможные состояния кругами, а возможные переходы из состояния в состояние обозначим стрелками. Мы считаем, что переход из S₀ в S₂ происходит только через S₁ или S₄, не может произойти мгновенно. Из состояния S₃ можно перейти только в состояние S₁ и обратно.

З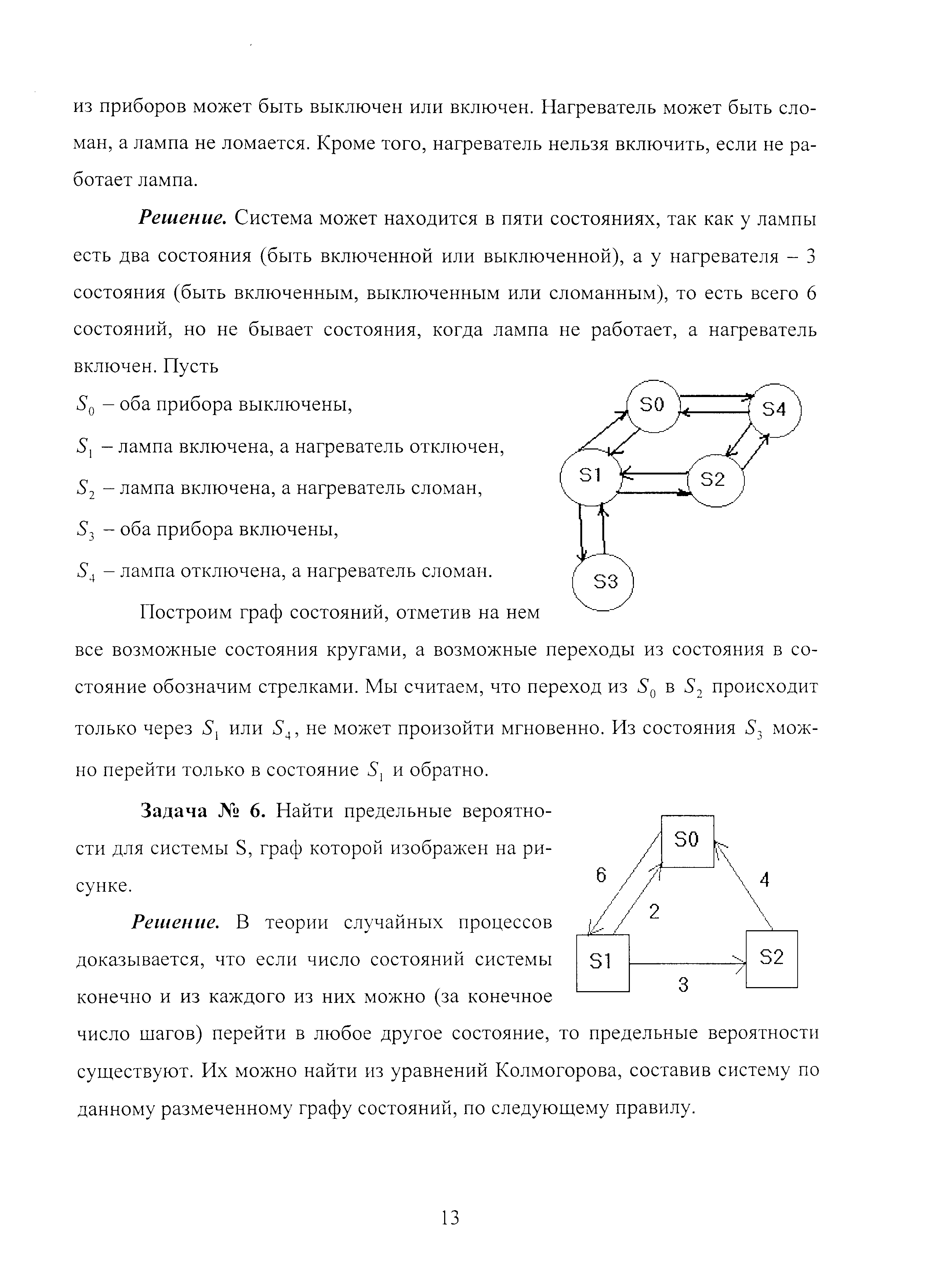адача №6. Найти предельные вероятности для системы S, граф которой изображен на рисунке.

Решение. В теории случайных процессов доказывается, что если число состояний системы конечно и из каждого из них можно (за конечное число шагов) перейти в любое другое состояние, то предельные вероятности существуют. Их можно найти из уравнений Колмогорова, составив систему по данному размеченному графу состояний, по следующему правилу.

Слева в уравнении стоит предельная вероятность данного состояния р_i,

умноженная на суммарную интенсивность всех потоков, ведущих из данного состояния, а справа — сумма произведений интенсивностей всех потоков, входящих в данное состояние, на вероятности тех состояний, из которых эти состояния выходят.

Кроме этого надо учитывать, что сумма всех вероятностей данной конечной системы равна единице. Составим уравнения для состояний S₁ и

S₂ (уравнение для состояния S₀— «лишнее»):

Решая систему, получаем

Ответ: Система примерно 32,25% времени пребывает в состоянии S₀, 38,71% ­– в состоянии S₁ и 29,04% времени находится в состоянии S₂

Задача №7. Найти валовой выпуск для сбалансированной многоотраслевой экономике в модели Леонтьева, если дана матрица прямых затрат А и вектор конечного потребления У:

Решение. Для сбалансированной многоотраслевой экономики выполняется следующее соотношение:

Х=А•Х+У,

где Х— вектор валового выпуска,

У— вектор конечного потребления,

А — матрица прямых затрат.

Нам дан вектор конечного потребления и матрица затрат. Надо найти валовой выпуск. Выразим валовой выпуск через конечное потребление и матрицу затрат:

X = (E – A)^-1 ∙Y

Нам следует найти матрицу, обратную к Е – А.

Найдем валовой выпуск:

Ответ: Валовой выпуск равен (5125; 5500).