Задание 9.17
Найдите по заданному
распределению
аргумента
функцию случайной величиныY=g(X)
и ее распределение
.
-
№
Y=g(X)
9
Если ξ — случайная величина с областью значений Хξ и функция f(x) определена на множестве Хξ, то η = f(x) — тоже случайная величина. Задача об отыскании функции распределения случайной
величины η по известной функции распределения случайной величины ξ легко решается, если f(x) — непрерывная монотонно возрастающая функция. В этом случае
Fη(x) = P(η<x) = P(f(ξ)<x) = P(ξ<f—1(x)) = Fξ(f--1(x)).
Итак, Fη(x)=Fξ(f--1(x)).
Здесь Fξ(x) — известная функция распределения случайной величины ξ, а символом f--1(x) обозначена функция, обратная к функции* f--1(x).
Плотность распределения случайной величины η для дифференцируемой функции f(x) находится по формуле
.
Решение:
Y
– принимает положительные значения,
при отрицательных значениях Y
распределение
равно нулю.
Задание 9.18
Найдите плотность
распределения вероятности суммы двух
независимых непрерывных случайных
величин, заданных своими плотностями
вероятностей
р1(х)
и p2(х).
Здесь Arctg[a]
-распределение арктангенса с плотностью
.
-
№
р1(х)
p2(х)
9
N(-1,1)
N(-1,2)
В теории вероятностей очень часто возникает необходимость в определении плотности вероятности суммы двух независимых случайных величин. Если ξ1 и ξ2 — непрерывные независимые случайные величины с плотностями вероятности соответственно р1(х) и p2(х), то плотность вероятностей суммы η=ξ1+ξ2 вычисляется по формуле
.
Интеграл такого вида называется сверткой функций р1(х) и р2(х).
Решение:
Задание 9.19
Найдите функцию распределения произведения двух зависимых случайных величин, распределенных равномерно в соответствии на промежутках [а, b] и [с, d].
|
N |
а |
b |
с |
d |
|
9 |
-1 |
4 |
-2 |
4 |
Решение:
-
непрерывная
случайная величина, где 
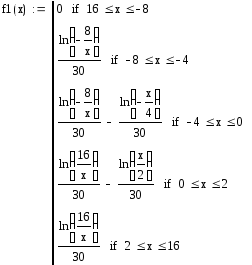
Плотность
распределения функции можно найти
простым дифференцированием функции
распределения случайной величины по
.
Задание 9.20
Вычислите математическое ожидание и дисперсию слyчайной величины Y = (X), которая представляет собой площадь указанной в задании геометрической фигуры, для случайной величины X, распределенной равномерно на промежутке [а, b].
-
№
Геометрическая фигура
а
b
9
Осевое сечение конуса с высотой Xи радиусом основанияX
9
11.5
Решение:
Так как случайная величина y является функцией случайной величины x, y=f(x), то
.
А дисперсия вычисляется по формуле
или Dy = Мy2 — (Мy)2