Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Дальневосточный Государственный Университет Путей Сообщения

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

КОНТРОЛ-САМОСТ задания по математике

.pdf

Скачиваний:

Добавлен:

13.04.2015

Размер:

821.96 Кб

Скачать

☆

1 / 101 2 3 4 5 6 7 8 9 10 > Следующая >>>

Министерство транспорта Российской Федерации Федеральное агентство железнодорожного транспорта ГОУ ВПО «Дальневосточный государственный университет путей сообщения»

Кафедра «Прикладная математика»

Е.П. Суляндзига

КОНТРОЛЬНЫЕ И САМОСТОЯТЕЛЬНЫЕ ЗАДАНИЯ ПО МАТЕМАТИКЕ

Сборник задач

Рекомендовано редакционно-издательским советом ДВГУПС

Хабаровск Издательство ДВГУПС 2007

УДК 51 (075.8) ББК В 11 я73 С 896

Рецензенты:

Кафедра «Высшей математики» Тихоокеанского государственного университета

(заведующий кафедрой доктор физико-математических наук, профессор

А.Г. Подгаев)

Заместитель директора по науке Вычислительного центра ДВО РАН, кандидат физико-математических наук

Н.Е. Ершов

Суляндзига, Е. П.

С 896 Контрольные и самостоятельные задания по математике [Текст] : сборник задач / Е. П. Суляндзига. – Хабаровск: Изд-во ДВГУПС, 2007. – 92 с.

Сборник задач соответствует Государственному образовательному стандарту ВПО направлений 140200 «Электроэнергетика», 140600 «Электротехника, электромеханика и электротехнологии», 190100 «Наземные транспортные средства».

Содержит задания для контрольных и самостоятельных работ по дисциплине «Математика» и включает темы, изучаемые в первом семестре: решение СЛАУ различными методами, типовые геометрические задачи, пределы, исследование функции вещественной переменной, неопределённый интеграл.

Рассмотрены примеры решения задач.

Задания могут быть использованы при самостоятельной работе, при выполнении домашних расчетно-графических работ, при проведении преподавателем аудиторных занятий, а также как варианты контрольных работ и как раздаточный материал при текущем и итоговом контроле знаний.

Предназначено для студентов первого курса дневной формы обучения.

УДК 51 (075.8) ББК В 11 я73

ВВЕДЕНИЕ

Общий курс математики является фундаментом математического образования специалиста. Преподавание математики в высших учебных заведениях имеет целью: формирование личности студентов, развитие их интеллекта и способностей к логическому и алгоритмическому мышлению; обучение основным математическим методам, необходимым для анализа и моделирования устройств, процессов и явлений.

Сборник содержит следующие задания по темам курса, изучаемым студентами в первом семестре: действия над матрицами и решение систем линейных алгебраических уравнений, типовые задачи аналитической геометрии, вычисление пределов, исследование непрерывности функции в точке, дифференцирование, нахождение первообразных различных функций.

Приведена методика выполнения различных задач, разобраны примеры, вызывающие у студентов определенные трудности, это поможет студенту в изучении тем курса, подготовке к тестированию.

Сборник содержит индивидуальные варианты самостоятельных и контрольных работ, предлагаемых для индивидуального решения, промежуточного или итогового контроля знаний. Выполнение заданий предполагает наличие соответствующих знаний и навыков по рассматриваемым темам, проработку рекомендуемой учебной литературы, в том числе и методических пособий автора.

1. Решение систем линейных алгебраических уравнений

Пример 1. Решить систему по правилу Крамера, матричным способом и методом Гаусса.

x + 3y + z = 9,
							+ 5z = 1,
2x − y							+ 5z = 1,
	+ 5y						− z = 8.
x	+ 5y						− z = 8.
Если det A ≠ 0, то система имеет единственное решение.
Правило Крамера.
a x + a y + a z											= b ,
11							12	13			1
a21x + a22 y + a23z = b2 ,
a x + a y + a z											= b .
31							32	33			3
Решение системы можно найти по формулам:
x =				x		, y =		y	, z =					z	,
x =						, y =			, z =						,
где				= DET A ≠ 0 – определитель матрицы системы;
x	– определитель, полученный из исходного																								заменой первого столбца
на столбец свободных членов;
y		– получен заменой второго столбца																					на столбец свободных членов
B;
z	– заменой третьего столбца столбцом свободных членов. Итак,
			1				3	1				−1 5							2 5					2	−1


=			2 −1 5						=1								− 3					+1					= −24 + 21+11= 8 ≠ 0.
			1				5	−1				5				−1			1	−1				1	5
			1				5	−1
Следовательно, система имеет единственное решение.
				9			3	1					−1 5					1 5					1		−1


x =				1 −1 5						= 9							− 3				+1					= −80,
				8			5	−1					5			−1		8		−1			8		5
				8			5	−1
y =					1		9	1	= 37,
					1		9	1
					2		1	5
					1		8	−1

	1	3	9
z =	2	−1 1		= 41.
	1	5	8
Ответ: x =			x = −80 = −10, y =		y	=	37	, z =	z =	41	.
Ответ: x =			x = −80 = −10, y =			=		, z =	z =		.
			8		8				8

Матричный метод. Будем искать решение как

Построим обратную матрицу A−1.

x
	= X = A−1B.
y	= X = A−1B.
z

A		=		−1 5							= −24 A = −					3 1					=		8 A =				3 1			=16,
A		=		−1 5							= −24 A = −					3 1					=		8 A =				3 1			=16,
11					5 −1								21			5 −1							31				−1 5
A = −						2 5					= 7		A =	1 1					= −2 A = −									1 1			= −3,
A = −						2 5					= 7		A =	1 1					= −2 A = −									1 1			= −3,
12							1 −1						22	1 −1									32					2 5
A =					2 −1					=11			A = −		1 3			= −2 A =								1 3			= −7,
A =					2 −1					=11			A = −		1 3			= −2 A =								1 3			= −7,
13					1			5					23		1		5						33				2 −1
							− 24					8	16
	−1		1
A		=						7				− 2	−3 . Теперь найдем столбец решений системы
A		=	8					7				− 2	−3 . Теперь найдем столбец решений системы
			8					11				− 2
								11				− 2	−7
									1			−24	8 16				9					1	− 24 9	+ 8 1+16 8									1	−80
X = A−1B =									1													1											1
												7	−2 −3				1			=			7 9 −2 1−3 8									=		37
									8			7	−2 −3				1			=		8	7 9 −2 1−3 8									=	8	37
									8													8			2 1−7 8								8
												11	−2 −7				8						11 9 −		2 1−7 8									41

Метод Гаусса.

Выпишем расширенную матрицу системы и приведем её к верхнему треугольному виду, чтобы на главной диагонали стояли единицы.

		1 3			1 9		1 3			1	9

A	=	2		−1	5 1	~1 шаг~	0		− 7 3		−17	~
A	=					~1 шаг~						~
1			1 5		−1 8			0 2		− 2	−1
			1 5		−1 8			0 2		− 2	−1

1 3		1		9		1 3		1		9			1 3		1			9
									3	17						3	17
			3	17				−							−
0 1		−				0 1							0 1
									7	7						7 7
					7
~		7				~ 2 шаг ~						~
	0 2	− 2			−1		0 0	−	8	−	41			0 0	1			41
																	8
									7	7									.

1-й шаг – 1-я строка «рабочая» и уже имеет a11 =1. Необходимо обнулить все элементы 1-го столбца ниже главной диагонали, для этого

–из второй строки вычли первую, умноженную на «2»;

–из третьей вычли первую строку;

–разделили 2-ю строку на «–7», чтобы получить элемент на главной

диагонали a22 =1.

2-й шаг – 2-я строка стала «рабочей», чтобы обнулить элементы ниже главной диагонали во 2-м столбце, необходимо из 3-й строки вычесть 2-ю,

умноженную на «2». Разделили 3-ю строку на «− 8 », чтобы получить a33 =1.

Запишем систему в привычном виде, двигаясь снизу вверх, последовательно выразим искомые переменные через уже найденные.

	41							41							41
z =			,				z =			,				z =		,
z =	8		,				z =	8		,				z =	8	,
	8							8							8
	3				17			3				17			37
	3				17			3				17			37
y −		z		=		,	y =		z		+		,	y =		,
y −	7	z		=	7	,	y =	7	z		+	7	,	y =	8	,
	7				7			7				7			8

x + 3y + z = 9							x = −3y − z + 9							x = −10.

Не забудьте сделать проверку – полученное решение должно обращать систему уравнений в тождество.

Ответ: x = −10, y = 37, z = 41.

Задача 1.

Решить систему по правилу Крамера, матричным способом и методом Гаусса.

x − y =1,	x + 2y + 5z = −4,

1) 2x + y + 2z = 0,	2) − x + y − 4z = 3,

5x − 4y + z = 4.	x + 4y + 6z = −5.

x	− y + z = 0,

3) 7x − 3y +10z = −3,

		= −1.
4x − 3y + 5z
6x + 4y + 5z		=1,
	+ y + z = 0,
4) x

5x + 3z = 2.
x	+ y + z = 0,
		= −2,
5) 3x + 8y + 5z
		= −1.
5x + 7y + 6z
x	+ 2y + 5z = −4,

6) − x + y − 4z = 3,
	2y + z = −1.

2x + y + 4z = −2,
		= −1,
7) 5x − 4y + 6z
	− y + z = 0.
x

4x + 7y + z = 3,

+ + =

8) 3x 3y z 2,

5x +10y + z = 4.

6x + 5y + z		= 5,
		= 4,
9) 5x + 3y + z

4x + z = 3.
	5x + 3y + z = 4,
10)
	6x + 5y + z = 5,

7x + 8y + z = 6.

	2x + y + 2z		= 0,
11)			= 4,
	5x − 4y + z
		− y = 1.
	x
	6x + 4y + z		= 5,
12)
	− 4x + y − z = −3,
			= 4.
	5x + 2y + z
	4x + 3y + 5z = −1,
13)
	7x + 3y +10z = −3,
		+ y + z = 0.
	x
	x	+ 3y + 5z	= −4,
14)
	− x − 4z = 3,
		+ 5y + 6z	= −5.
	x
	6x + 7y + 5z = 1,
15)
	5x + 8y + 3z = 2,
		+ y + z = 0.
	x
	x	+ 2y = 1,
16)			= 4,
	5x + 2y + z

	4x − y + z = 3.
	5x + 2y + z		= 4,
17)
	4x − y + z = 3,
			= 5.
	6x + 4y + z
	x	+ y + z = 0,
18)
	10x + 3y + 7z = 3,

5x + 3y + 4z = 1.

	5x + 4y + 6z = −1,
19)
	3x + 5z = −2,
		+ y + z = 0.
	x
	x	+ 3y	+ 5z = −4,
20)		+ 8y	+ 7z = −6,
	x
		+ 5y	+ 6z = −5.
	x
	2x + 5y + z = 1,
21)		− 4y	− z = 2,
	x
			= 2.
	2x + y
	2x + 5y + z = 1,
22)		− 4y	− z = 2,
	x

	4x + 6y + z = 3.
	x	+10y + 5z = −4,
23)		+ 3y	+ 3z = −2,
	x
		+ 7y	+ 4z = −3.
	x
	6x + y		+ 5z = 1,
24)			= 4,
	4x + y
			+ 3z = 2.
	5x + y
	5x + 6y + 7z = −2,
25)
	3x + 5y + 8z = −5,
		+ y + z = 0.
	x
	x	+ 5y	+ 4z = −3,
26)
	2x + 2y − z = 3,
		y	+ z = −1.

	6x − 4y + 5z = 1,
27)		= 2,
	4x + y + 2z

	x − y + z = 0.
	4x + 3y + 5z = −1,
28)
	7x + 3y +10z = −3,

	x + y + z = 0.
	6x + 5y + 4z = 2,
29)
	5x + 3y = 5,

	x + y + z = 0.
	6x + 5y + z	= 5,
30)		= 6,
	7x + 8y + z
		= 4.
	5x + 3y + z
	x − y + z = 0,
31)		= −2,
	2x + y + 4z

	5x − 4y + 6z = −1.
	5x + 3y + z	= 4,
32)
	4x + z = 3,
		= 5.
	6x + 5y + z
	x − y + z = 0,
33)
	3x + 5z = −2,

5x − 4y + 6z = −1.

	x + y − z = 2,
34)		= 4,
	3x + 8y − z

	5x + 7y − 4z = 9.
	7x + 8y + z	= 6,
35)
	4x + y + z = 3,
		= 4.
	5x + 3y + z
	x + y − z = 2,
36)		= 4,
	3x + 8y − z
		= 5.
	2x − y − 3z

x + 9y + 2z = −1,

− − =

37)2x y 3z 5,

3x − 4z = 7.

	3x + 7y = 3,
38)
	4x + y + z = 3,
		= 4.
	5x + 3y + z
	3x + y + 4z	= −1,
39)			= −1,
	7x − 6y + 8z
			= −1.
	2x + 3y + 3z
	x − y − z = 2,
40)		= 9,
	5x − y − 4z
			= 5.
	2x − 7y − 3z

2. Приведение пятичленного уравнения к каноническому виду

Пример 2. Привести уравнение кривой к каноническому виду

− 4x2 + y2 +12x + 4y − 7 = 0.

Решение. Выделить полные квадраты по переменным x и y

− 4( x2 − 3x )+ y2 + 4y − 7 = 0,
	3	2	9	2
	3		9	2
− 4 x −		−		+ (y + 2) − 4	− 7	= 0,
− 4 x −		−		+ (y + 2) − 4	− 7	= 0,
	2		4


				3	2						2
−	4 x −						+ 9 +		(y +		2) −11	= 0,
−	4 x −			2			+ 9 +		(y +		2) −11	= 0,
				2
				3	2					2
−	4 x −						+ (y + 2)				= 2 – разделить на «2»,
−	4 x −			2			+ (y + 2)				= 2 – разделить на «2»,
				2
			3 2
	x −						(y	+	2
	x −								2
−			2			+			2)	= 1,
−		1				+		2		= 1,
		1						2
		2

			3		2
	x −						(y + 2)2
	x −		2
			2
−		1		2		+	(		)2 =1 – получен канонический вид кривой; это
−		1		2		+	(	2	)2 =1 – получен канонический вид кривой; это


		2
		2

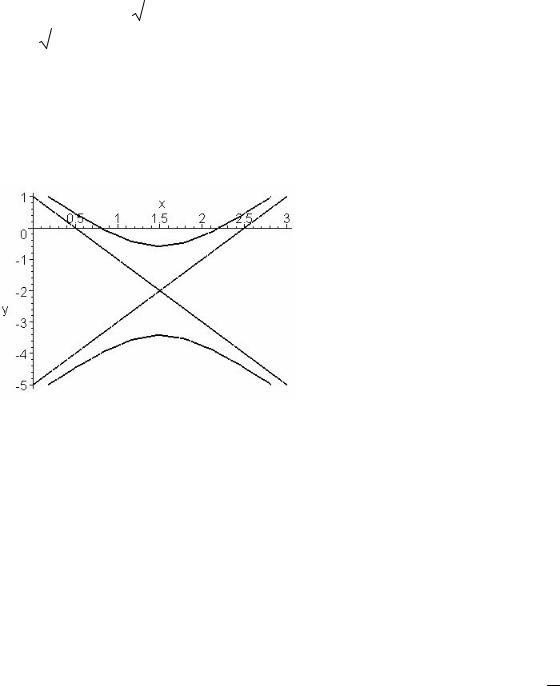
гипербола, которая:

– возлежит, пересекая ось oy ;

		3
– имеет асимптоты y + 2	= ±2 x −		.
– имеет асимптоты y + 2	= ±2 x −	2	.
		2

Сделаем чертеж:

Задача № 2. Привести уравнение кривой к каноническому виду. Сделать чертеж.

1)		9	x		2		− y			2		−		9		x − 2y		−	31		= 0		8)	9x	2	− 4y		2	− 9x + 8y		−		151		= 0
1)		4	x				− y					−		2		x − 2y		−	4		= 0		8)	9x		− 4y			− 9x + 8y		−			4	= 0
		4												2					4															4
2)		x2			− y				2	−			3		x − 6y −			119			= 0		9)	4x	2	− y	2	+16x − 6y			+11= 0

	16											8						16

																								− y2 + 6x − 6y −12 = 0
3)		25		x		2		− y			2	+			25		x − 3y + 29 = 0						10)	− y2 + 6x − 6y −12 = 0
3)	16			x				− y				+		4			x − 3y + 29 = 0						11)	x2 + y2 − x + 6y +						21		= 0
	16													4

																				47
4)	9x2 + 4y2 − 27x − 8y −																			47		= 0							4
4)	9x2 + 4y2 − 27x − 8y −																					= 0							4

412) x2 + y2 + 4x + 3y + 9 = 0

		9											4
5)	x2 +	9	y2 − 4x + 9y + 4 = 0						9x	2	+ 4y	2	− 9x − 8y −	119		= 0
5)	x2 +		y2 − 4x + 9y + 4 = 0					13)		2		2		119
	4							13)							4
	4
	x2 − y2 − x − 6y −			51
6)				51		= 0
6)						= 0			4x2 + y2 +16x + 6y + 21= 0
	4							14)	4x2 + y2 +16x + 6y + 21= 0
7)	x2 − y2 + 4x − 3y +				23		= 0	15)	− y2 + 6x + 4y + 8 = 0
7)	x2 − y2 + 4x − 3y +						= 0	15)	− y2 + 6x + 4y + 8 = 0
	4

1 / 101 2 3 4 5 6 7 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.03.201616.64 Mб1764Конструкция Вагонов.pdf
#
11.12.2015186.37 Кб33Консьюмеризм защита прав потребителей.doc
#
16.03.2016352.58 Кб51конт работа.pdf методы оптимальных решений.pdf
#
16.03.2016157.21 Кб8Контр.работа социально-эк направления развития.pdf
#
16.03.2016120.09 Кб10Контр.работа № 1.pdf
#
13.04.2015821.96 Кб28КОНТРОЛ-САМОСТ задания по математике.pdf
#
11.12.2015375.3 Кб52Контроль калибра-скобы.doc
#
16.03.201642.74 Кб22контрольная .docx
#
13.04.201521.11 Кб43Контрольная работа НОРМЫ.doc
#
11.12.201550.08 Кб16Контрольная.docx
#
07.07.201923.79 Кб5Конфликтология (лекции).docx