Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Дальневосточный Государственный Университет Путей Сообщения

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

КОНТРОЛ-САМОСТ задания по математике

.pdf

Скачиваний:

Добавлен:

13.04.2015

Размер:

821.96 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 107 8 9 10 > Следующая >>>

− n n 4 n + 5

LIM

3 + 2 n 9 n3 + n

n → ∞

Вариант

x4 + x − x3 − 1

x2 − 5 x + 6

LIM

+ x − 3

x + 1 − 10

− 2 x

x → 1 2 x2

x → 3

1 + COS(x)

x + 2

LIM

+ 7 x + 6

(4 x + 5)

x → π

+ COS(x)

LIM

SIN

x → (-1)

LIM

(3 n(2/3) + 1) ( n − 1 + 4)

(n + 4)2 (9 n − 2)

n → ∞

Вариант

LIM

3 x2 − x − 2

LIM

x2 − 3 x + 2

x + 8 − 2 x + 7

x → 1 2 x2 + x − 3

x → 1

x + 2

SIN(x)

− x − 2

LIM

1 − 1 + SIN(x)

x +

x → π

LIM

x → 2

LIM

(4 n + 2)2 n

n → ∞

( n + 4)

n + 1

Вариант

LIM

2 x2 + x − 3

LIM

x2 − 2 x − 8

− 2 x2 − x + 2

x + 12 − 2 x + 8

x → 1 x3

x → 4

x + 4

(3 x)

1 − E

+ 6 x +

LIM

(x + 2)

LIM

SIN(x) − SIN(2 x)

x → 0

x → (-1)

			3		2
							3
				+ 1		( n	+ 4)
			n	+ 1		( n	+ 4)
	LIM		2
	n → ∞ 3 + 2 n 9 n3 + n
Вариант		2 x2 + x − 3								x2 − x − 6
44	LIM							LIM
	x → 1 x3 + x − x2 − 1							x → 3	x + 1 − x2 − 5
						1		2	−	1 + 3 COS(x)
								2	−	1 + 3 COS(x)
					2	+ 2 x −		LIM
		(x2 −		x		+ 2 x −	8	LIM	COS(3 x) − Ex
	LIM	(x2 −		3)				x → 0	COS(3 x) − Ex
	x → 2
	LIM			(n + 4)2 (9 n − 2)
	LIM					3		2
						3
	n → ∞ (3 n(2/3) + 1) ( n −
	n → ∞ (3 n(2/3) + 1) ( n −							1 + 4)

Вариант

2 x2 − 7 x + 3

x2 + x − 2

LIM

x + 3 − 9

− 5 x

x → 3 x3 − 5 x − 12

x → 1

SIN(3 x) + SIN(x)

LIM

LN(1 − SIN(2 x))

− 10 x − 11

x → 0

LIM

(3 x2 − 2) x

x → (-1)

− n

4 n + 5

LIM

(4 n

+ 2)2

n → ∞

Вариант

9 x2 − 19 x + 2

x − x + 12

LIM

x → 2 x3 + x − 2 x2 − 2

x → 4 x2 − 6 x + 8

2 x + 3

LN(COS(2 x))

LIM

− 8 x + 12

LIM

(3 x −

5) x

x → π

x → 2

SIN

x + COS(x)

( n + 4)

n + 1

LIM

n → ∞ (n + 4)2 (9 n − 2)

Вариант

9 x2 − 19 x + 2

x − x + 6

LIM

x → 2 x3 + x2 − 4 x − 4

x → 3 x2 − 5 x + 6

1 + COS(x)

LIM (1 + LN(1 −

LIM

5 x))

1 + COS(x) + SIN(5 x)

x → π

x → 0

(3 n(2/3) + 1) ( n − 1 + 4)

LIM

3 + 2 n 9 n3 + n

n → ∞

Вариант

9 x2 − 19 x + 2

COS(3 x) − Ex

LIM

4 x2

− 9 x + 2

LIM

LN(1 − SIN(2 x))

x → 2

x → 0

x + 3 − 2 x

LIM

− 10 x − 11

x2 − 3 x + 2

x → 1

LIM

(x2 )

x → (-1)

4 n + 5

− n n

LIM

+ 4)2 (9 n − 2)

n → ∞ (n

Вариант

x3 + x − 2 x2 − 2

LIM

COS(x) − COS(5 x)

LIM

x3 + 4 x − 2 x2 − 8

ESIN(x) − 1

x → 2

x → 0

− 8 x

+ 16

2 x + 3

LIM

− 8 x

x + 12 −

2 x + 8

COS(x −

x → 4

LIM

x → 2

(3 n(2/3)

+ 1) ( n −

LIM

1 + 4)

(4 n + 2)2 n

n → ∞

Вариант

x3 + x − 2 x2 − 2

SIN(x)3

LIM

− x + 2

LIM

x → 2 x3 − 2 x2

x → π x2 − π2

− 7 x + 12

LIM

− 1

x + 1 −

x2 − 5

COS(x −

x → 3

LIM

x → 1

LIM

3 + 2 n

9 n3 + n

n → ∞

+ 1

( n + 4)

Вариант

− 5x + 6

LN(1+ 2x2 )

LIM

− 8

LIM

SIN2 3x

x→2

x→0

3 + x2 − 2x

3x x2 + 5x −1

LIM

x2 −1

LIM

(x 3 −1)2

x→1

x→∞

3x −

5 3 x+90

LIM

x→ 3x +

5. ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

Пример 10. Дана y(x) =		1		, найти y'(x) = ?
		2
	LN(x		+ 5x)

Решение. Чтобы верно найти искомую производную, запишем функцию в

виде y(x) = (LN(x2 + 5x))−1. Тогда ищем производную как производную сложной функции – как степенной умножить на производную логарифма и умножить на производную подлогарифмического выражения:

y'(x) = −(LN(x2 + 5x))−2		2x + 5			.
y'(x) = −(LN(x2 + 5x))−2					.
		x2 + 5x
	3
				(x3 + 4x +1)
Пример 11. Дана y(x) =	(x −1)5			(x3 + 4x +1)			, найти y'(x) = ?

			3x +	1(x2		− 2x)3
			3x +	1(x2		− 2x)3

Решение. Чтобы найти производную такой сложной функции, удобно использовать логарифмическую производную, а именно логарифмируем обе части выражения и используем свойства логарифма:

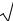
LN y =	3	LN(x −1) + LN(x3 + 4x +1) −	1	LN(3x +1) − 3LN(x2 − 2x),

5		2
дифференцируем обе части выражения

3x2 + 4

−

− 3

2x − 2

, умножим обе части

y 5 x −1 x

+ 4x +1 2 3x +1

x2 − 2x

равенства на y, тем самым будет найдена искомая производная

3x2

+ 4

2x − 2

y =

−

x −1

+ 4x +1

2 3x +1

− 2x

Ответ:

3x2

(x −1)

(x3 + 4x +1)

+ 4

2x − 2

y'=

−

x −1

+ 4x +1

2 3x +1

3x +1(x

− 2x)

− 2x

Пример 12. Дана y(x) = COS

2 πx

, найти y'(x) = ?

Решение. Пример, при выполнении которого возникает типичная ошибка

утери производной как производной сложной степенной функции, чтобы

избежать ошибки, перепишем y(x) = COS

πx

πx 2

. Найдем

COS

производную y'(x) =

πx

– производную степенной

2 COS

− SIN

функции умножить на производную косинуса (аргумент прежний), умножить на производную аргумента.

Пример 13. Найти производную параметрически заданной функции «Де-

3at

x =

1+ t

картов лист»

3at2

y =

,a > 0

1+ t

Решение. x'

1+ t3 − t 3t

= 3a

1− 2t

, производную y' , учитывая,

(1+ t3 )2

что y = tx.

y' = x

+ tx'

3at

+ 3at

1− 2t

3at

1+ t3

+1− 2t3

= 3at

2 − t

(1+ t3 )2

1+ t3

		=	y'	=	t(2 − t	3 )
Ответ: y'	x		t				.
			x't		1− 2t	3

Пример 14. Найти производную неявно заданной функции

x3 + y3 − 3axy = 0, a > 0.

Решение. 3x2 + 3y2 y'−3a(y + xy') = 0, выразим y'= ay − x2 .

y2 − ax

Примечание. В примерах № 13, 14 вычислены производные одной функции, заданной разными способами. Сверьте ответы.

5.1. Асимптоты

Данная тема вызывает трудности и требует навыков.

При исследовании функции возникает вопрос о её поведении на бесконечности (горизонтальные или наклонные асимптоты) и вблизи точек разрыва (вертикальные):

–вертикальные асимптоты ищем, если есть точки разрыва функции;

–горизонтальные асимптоты ищем при стремлении x на бесконечность;

–наклонные асимптоты возможны, если нет горизонтальных;

–функция может вообще не иметь асимптот, т. е. LIM f (x) = ∞, или

x→∞

LIM f (x) = A. x→a

1. Вертикальные асимптоты? (возможны, если функция имеет точки разрыва II рода)

при x → a		LIM f (x) = ±∞
(рассматривать	f (x) → ±∞ , т. е.	LIM f (x) = ±∞
односторонние		x→a
пределы)
(когда аргумент стремится в конечному значению,
функция стремится к ∞)

Функция имеет вертикальную асимптоту x = a
2. Горизонтальные асимптоты?

при x → +∞	f (x) → A, т. е.	LIM f (x) = A
		x→+∞
		Когда аргумент
		стремится к ∞,

		функция – к конечному
		значению

Функция имеет горизонтальную асимптоту y = A при x → +∞
при x → −∞	f (x) → B, т. е.	LIM f (x) = B
		x→−∞
		Когда аргумент
		стремится к ∞,
		функция – к конечному
		значению

Функция имеет горизонтальную асимптоту y = B при x → −∞

Если нет горизонтальных асимптот

ищем

3.Наклонные асимптоты?

k = LIM

f (x)

при x → +∞

f (x) → kx + b, т. е.

x→+∞

b = LIM ( f (x) − kx)

x→+∞

Функция имеет наклонную асимптоту y = kx + b при x → +∞

( при x → −∞ действовать аналогично )

Пример 15. Определить асимптоты функции y(x) =

x2 −1

Решение. 1) ООФ (−∞;−1) (−1;1) (1;+∞). В точках разрыва функции

есть вертикальные асимптоты. Проверим это.

x1 = −1

e−1−α

x = −1−α

LIM

= LIM

2 −1

α → 0

x→−1−0 x

α →0 (−1−α)

2 −1 α →0α2 + 2α

= LIM

e−1−α

e−1

= +∞

α(α + 2)

α →0

+ 0

LIM

x = −1+α

= LIM

e−1+α

= LIM

e−1+α

e−1

= −∞,

2 −1

(α − 2)α

− 0

x→−1+0 x

α → 0

α →0 (α −1)2

−1 α →0

это значит, что x = −1 – вертикальная асимптота.

x1 = 1

LIM

x = 1−α

= LIM

e1−α

LIM

e1−α

α → 0

α2 − 2α

x→1−0 x2 −1

α →0 (1−α)2 −1

α →0

= LIM

e1−α

= −∞

α →0α(α −

− 0

LIM

x = 1+α

= LIM

e1+α

LIM

e1+α

= +∞ ,

(α + 2)α

+ 0

x→1+0 x2 −1

α → 0

α →0 (α +1)2 −1

α →0

следовательно, x = 1 – вертикальная асимптота.

2) Выясним, есть ли горизонтальные асимптоты.

LIM

e−∞

= 0, следовательно,

2 −1

x→−∞ x

∞

y = 0 - горизонтальная асимптота при x → −∞ .

LIM

= LIM

= +∞ – на + ∞ нет горизонтальной

2 −1

x→+∞ x

x→+∞ 2x

x→+∞

асимптоты.

3) Очевидно, что при x → +∞ наклонной асимптоты нет, а именно:

LIM

y(x)

= LIM

= +∞.

(x2 −

x→+∞

1)x x→+∞

3x2 −1

Ответ: x = −1, x = 1 – вертикальные асимптоты, y = 0 – горизонтальная

асимптота при x → −∞ .

Пример 16. Определить асимптоты функции y(x) =

x2 +1

x − 2

Решение. 1) очевидно, что функция терпит разрыв в (.) x = 2, и это будет

вертикальная асимптота:

LIM

x2 +1

= 2 −α

= LIM

(2 −α)2 +

= LIM

(2−α)2 +

= −∞

x − 2

α → 0

−α

− 0

x→2−0

α →0 2−α − 2

α →0

LIM

x2 +1

x = 2 +α

LIM

(2 +α)2 +1

LIM

(2+α)2 +

= +∞ .

−

α → 0

− 2

+α

+ 0

x→2+0 x

α →0 2+α

α →0

2) Проверим, есть ли горизонтальные асимптоты.

LIM

x2 +1

= LIM

= ±∞ – горизонтальных асимптот нет, надо искать

x→±∞ x − 2

x→±∞ 1

наклонные.

3) LIM

y(x)

x2 +1

= 1

= k ,

LIM

2)x

x→±∞

x→±∞ (x −

x→±∞ 2x − 2

x→±∞ 1

2 +1

2x +1

LIM y(x) − kx =

LIM

− x

= LIM

= 2

= b, а это значит,

x→±∞

x→±∞ x − 2

x→±∞

x − 2

что прямая y = x + 2 есть наклонная асимптота при x → ±∞ .

Ответ: x = 2 – вертикальная асимптота, y = x + 2 – наклонная асимптота при x → ±∞ .

Задача № 5. Выполнить задания:

1)найти y'(x);

2)найти логарифмическую производную функции y = u(x)v(x);

3)найти производную неявно заданной функции;

4)найти y'x , y"xx параметрически заданной функции;

5)исследовать функцию.

ВАРИАНТ 1

2y −

x + y

= (x + 2y)e3x

y(x) = eSIN2 3x COS(x3 − x)

x = (t + 3)t

+ 4)et

y = (2t

11 (5+

)

LN x

f (x) =

1+ 2x

y(x) = 2x +

1− x

ВАРИАНТ 2

+ 2 = xy − y

(x + 3) LN(x

− 4x)

y(x) =

x = COSt + e

3x + 2x

COS

y = SIN 2t − e

y(x) = (ex/3 + SIN(4x2 +1))1/LN x

f (x) =

2 +1

ВАРИАНТ 3

exy + xe2y =10x2 − y2

				3
y(x) = COS3 (2x +1) SIN			x = t		+1
y(x) = COS3 (2x +1) SIN	πx −1	4
				2
			y = t	2	SIN t
			y = t		SIN t

y(x) = (tg(7x −1) +

)3x+2 5

f (x) =

+ x2

1− x

ВАРИАНТ 4

= ARCSIN

(3x +1)4/7 x

2 + 4x

y(x) =

x =

+ 1, y =

(x2 +1)3(ex

−1)4

t + 1

y(x) = (LN(2x + 5))arctgx

f (x) =

LN x

ВАРИАНТ 5

x − y = ex+ y2 + xy

y(x) = SIN3(x +

x = LNt

x) LN(SIN(x +1))

y = tCOSt

y(x) = (COS(x2 + x +1))tg(x−1)

f (x) = LN(x2 + 4) − x2

ВАРИАНТ 6

y2 COS x + xSIN y = 3

y(x) =

COS(LN(

x + 2))

x = tCOSt

x2 − 3x + 2

y = SIN 2t

y(x) = (x3 + x2 − x −1)ARCSIN(3x−1)

f (x) = e−x x2

ВАРИАНТ 7

arctg

= y − 2x2

= t

(COS

3x + SIN 2x)

y(x) =

COS x + 4

= t

t +1

y(x) = (SIN 2x)LN(x

+4)

f (x) = xLN x

ВАРИАНТ 8

2COS(x2 + y) + SIN(x + y2)

<<< < Предыдущая 1 2 3 4 5 67 / 107 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
16.03.201616.64 Mб1768Конструкция Вагонов.pdf
#
11.12.2015186.37 Кб33Консьюмеризм защита прав потребителей.doc
#
16.03.2016352.58 Кб52конт работа.pdf методы оптимальных решений.pdf
#
16.03.2016157.21 Кб8Контр.работа социально-эк направления развития.pdf
#
16.03.2016120.09 Кб10Контр.работа № 1.pdf
#
13.04.2015821.96 Кб28КОНТРОЛ-САМОСТ задания по математике.pdf
#
11.12.2015375.3 Кб52Контроль калибра-скобы.doc
#
16.03.201642.74 Кб22контрольная .docx
#
13.04.201521.11 Кб43Контрольная работа НОРМЫ.doc
#
11.12.201550.08 Кб16Контрольная.docx
#
07.07.201923.79 Кб5Конфликтология (лекции).docx