7. Применение производной для исследования свойств функций.

7.1. Возрастание и убывание функций

Функция называетсявозрастающей (убывающей) на некотором интервале , если большему значению аргумента из этого интервала соответствуетбольшее (меньшее) значение функции, т. е. при выполняется неравенство.

И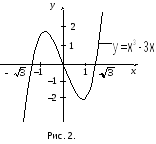нтервалы, в которых функция возрастает или убывает, называются интервалами монотонности функции.

Рассмотрим применение производной для нахождения интервалов монотонности функций.

Теорема 1 (достаточное условие возрастания функции). Если функция непрерывна на отрезкеи дифференцируема на интервале, причем() для любого, то эта функция возрастает (убывает) на отрезке.

Пример 7.1. Исследовать на монотонность (т. е. возрастание и убывание) функцию:

Решение.

.

Неравенство , т. е.,справедливо для x<–1 и для x>1. Следовательно, функция возрастает на интервалах(–, –1) и (1, +).

Поскольку неравенство , т. е. справедливо для

x(–1, 1), то на интервале (–1, 1) функция убывает.

7.2. Экстремумы функции

Дадим точные определения точкам максимума и минимума функции. Пусть функция определена на промежутке X и x₀X. Говорят, что в точке x₀ функция имеет максимум (минимум), если существует такая окрестность точки x₀, что для любого x из этой окрестности ().

Точки максимума и минимума называются точками экстремума.

Замечание 1. Точки экстремума всегда являются внутренними точками промежутка, т. е. не могут быть его концом.

Теорема 2 (необходимое условие экстремума). Если функция дифференцируема в точке x₀ и некоторой ее окрестности и x₀ – точка экстремума, то .

Следствие. Если x₀ – точка экстремума, то илине существует.

В качестве примера приведем функцию (рис. 3).

Рис. 3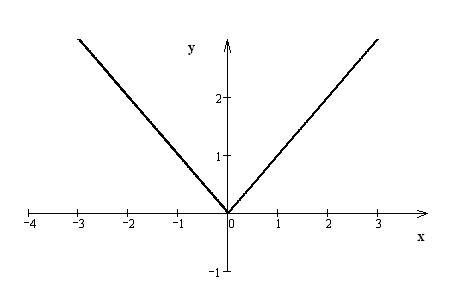

Очевидно, что x₀ = 0 является точкой минимума, так как |0| < |x| для любого x ≠ 0. А в точке x₀ = 0 производной не существует.

Если илиf'(x₀) не существует, то точку x₀ будем называть критической (или подозрительной на экстремум). Критическая точка может и не быть точкой экстремума.

Теорема 3 (первое достаточное условие экстремума). Пусть функция определена и непрерывна в точкеx₀ и некоторой ее окрестности, дифференцируема в этой окрестности, за исключением, быть может самой точки x₀, и точка x₀ – критическая точка для функции (т. е.илине существует). Тогда:

1) если при x < x₀ производная , а дляx > x₀: , тоx₀ – точка максимума;

2) если при x < x₀: , а приx > x₀: , тоx₀ – точка минимума.

Пример 7.2. Исследовать на монотонность и экстремумы функцию . Построить её график.

Решение.

Заданная функция определена и непрерывна на всей числовой оси . Найдем производную:.

Тогда приx₁=0 и x₂ =2. Точки x₁, x₂ – критические точки. Эти точки разбивают всю числовую ось на три интервала: (–; 0), (0; 2), (2; +). Составим таблицу, в первой строке которой поместим указанные точки и интервалы, во второй строчке – сведения о производной в точках и на интервалах, а в третьей – поведение данной функции(табл. 2).

Таблица 2

x		0	(0, 2)	0
		0		0
	убывает		возрастает		убывает

Определим знак на каждом из интервалов: еслиx(–, 0), то ; еслиx(0, 2), то ; еслиx(2, + ), то . Отсюда определяется поведение функции : на первом и последнем интервалах функция убывает, а на втором – возрастает (рис.4).

y(x)=x²e^-x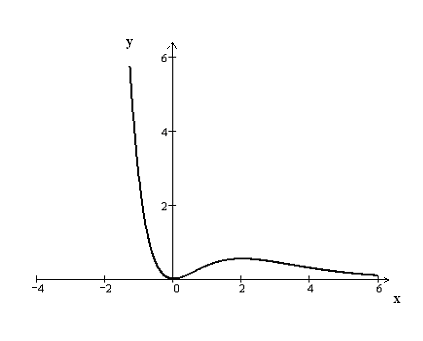

Рис. 4

Отсюда следует, что x₁= 0 является точкой минимума,, аx₂ =2 – точка максимума,.