
- •Дифференциальное исчисление функций одной переменной
- •Введение
- •1. Понятие производной, её геометрический смысл
- •1.1. Понятие производной
- •1.2. Геометрический смысл производной
- •2. Правила дифференцирования. Производная сложной функции
- •2.1. Правила дифференцирования
- •2.2. Производная сложной функции
- •3. Дифференциал функции
- •4. Дифференцирование обратной функции, функций заданных неявно, параметрически. Логарифмическое дифференцирование
- •4.1. Дифференцирование обратной функции
- •4.2. Дифференцирование функций, заданных неявно
- •4.3. Дифференцирование функций, заданных параметрически
- •4.4. Логарифмическое дифференцирование
- •5. Производные высших порядков
- •5.1. Понятие производной высшего порядка
- •5.2. Производные высших порядков от функций, заданных параметрически
- •5.3. Производные высших порядков от функций, заданных неявно
- •6. Правило Лопиталя
- •7. Применение производной для исследования свойств функций.
- •7.1. Возрастание и убывание функций
- •7.2. Экстремумы функции
- •7.3. Наибольшее и наименьшее значения функции на отрезке
- •7.4. Выпуклость, вогнутость графика функции, точки перегиба
- •7.5. Асимптоты
- •8. Построение графиков функций с помощью элементов дифференциального исчисления
- •9. Расчетно-графическое задание Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Вариант 11
- •Вариант 12
- •Вариант 13
- •Вариант 14
- •Вариант 15
- •Вариант 16
- •Вариант 17
- •Вариант 18
- •Вариант 19
- •Вариант 20
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 28
- •Вариант 29
- •Вариант 30
- •Библиографический список
- •Оглавление
- •Дифференциальное исчисление функций одной переменной
- •Отпечатано методом прямого репродуцирования
- •6 80021, Г. Хабаровск, ул. Серышева, 47
2. Правила дифференцирования. Производная сложной функции
2.1. Правила дифференцирования
Правила дифференцированияпозволяют находить производные суммы (разности), произведения и частного двух функций:
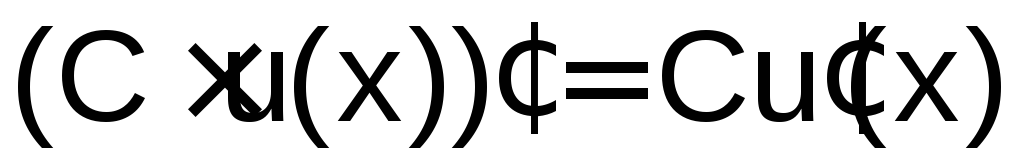 .
.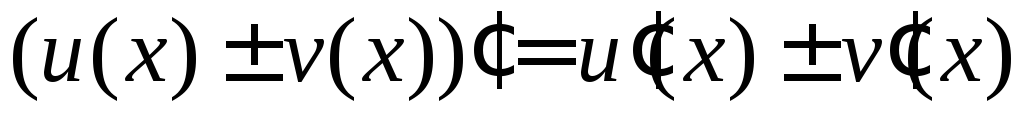 .
.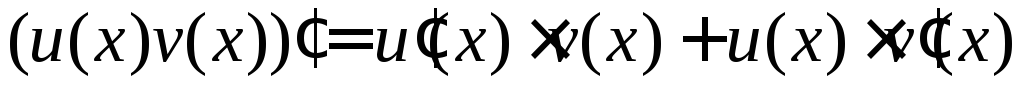 .
.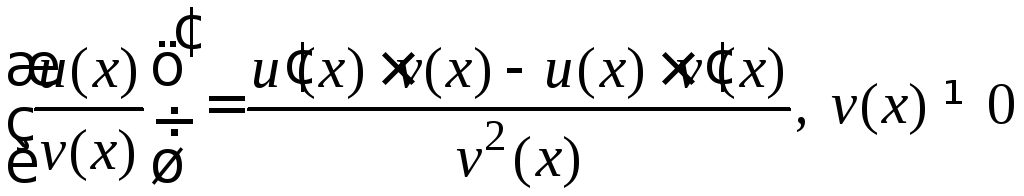 .
.
Замечание. Свойство 2 выполняется для алгебраической суммы любого количества функций.
Пример
2.1.
Пользуясь формулами дифференцирования,
найти производные следующих функций:
а)
![]() ;
б)
;
б)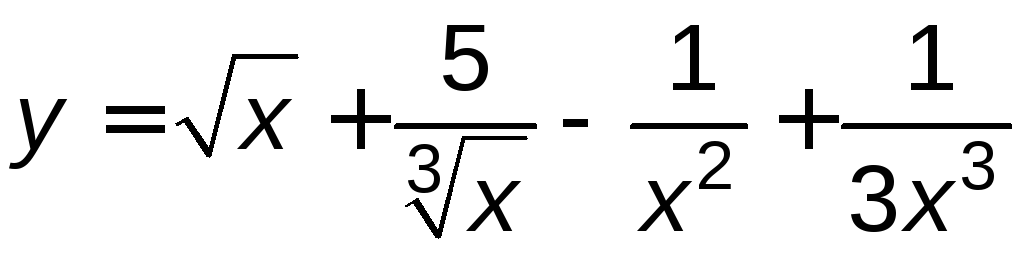
Решение.
а) Используя таблицу производных, первое и второе свойства получим:
![]() ;
;
б) Вводя дробные и отрицательные показатели, преобразуем данную функцию:
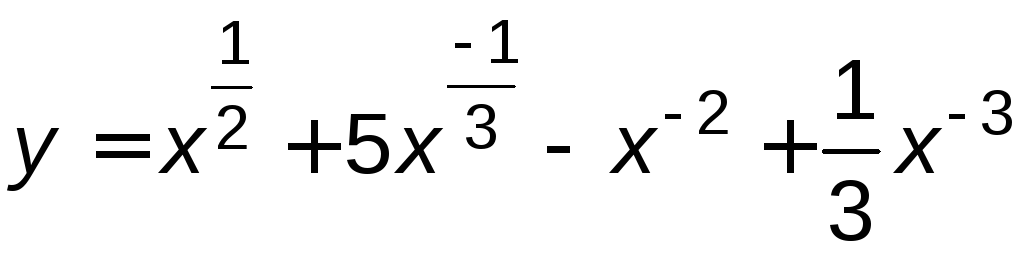 .
.
Тогда, используя производную степенной функции, свойства 1 и 2 будем иметь:
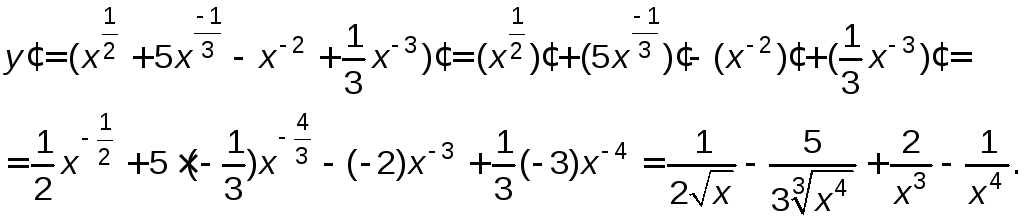
Пример
2.2.
Найти производную функции
![]() :
:
Решение.
Воспользовавшись свойством 3 получим:
![]()
Пример
2.3.
Найти производную функции
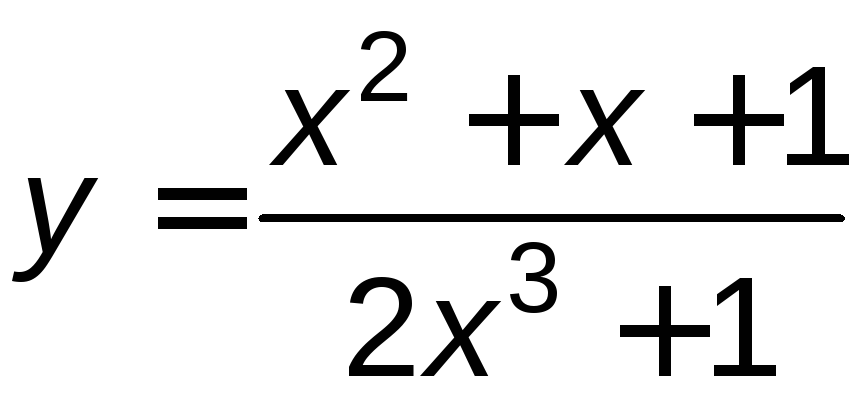 .
.
Решение.
Для решения примера используем свойство 4 производных.
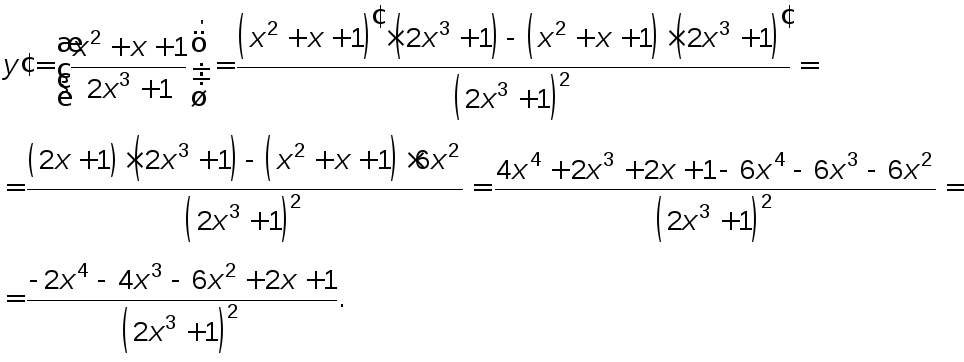
2.2. Производная сложной функции
Рассмотрим дифференцирование сложной функции.
Пусть
![]() являетсясложной
функцией,
составленной из функции
являетсясложной
функцией,
составленной из функции
![]() ,
,![]() ,
гдеu
– промежуточный аргумент. Покажем, как
найти производную сложной функции, зная
производную для функции
,
гдеu
– промежуточный аргумент. Покажем, как
найти производную сложной функции, зная
производную для функции
![]() (её будем обозначать через
(её будем обозначать через![]() )
и производную
)
и производную![]() для функции
для функции![]() .
.
Теорема
1.
Если функция
![]() имеет производную
имеет производную![]() в точкеx,
а функция
в точкеx,
а функция
![]() имеет производную
имеет производную![]() в
точке
в
точке![]() (
(![]() ),
то сложная функция
),
то сложная функция![]() в точкеx
имеет производную
в точкеx
имеет производную
![]() ,
причем
,
причем
![]() =
=
![]()
![]() .
.
Иначе, производная сложной функции равна произведению производной данной функции по промежуточному аргументу на производную промежуточного аргумента.
Пример
2.4.
Найти производную функции
![]() .
.
Решение.
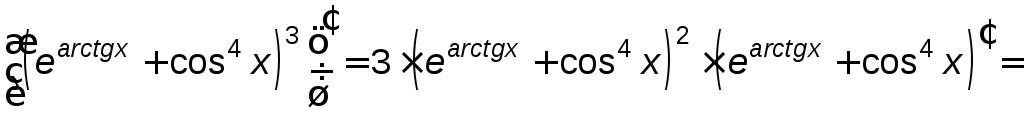
![]()
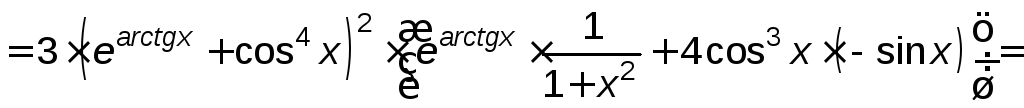
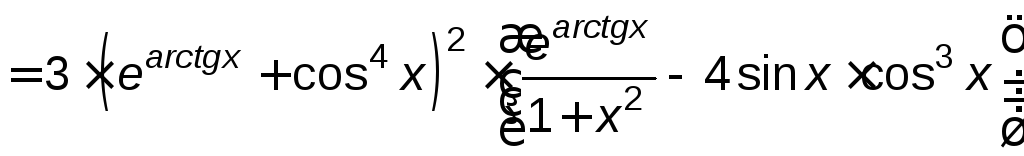 .
.
Пример 2.5. Найти производную функции
![]() .
.
Решение.
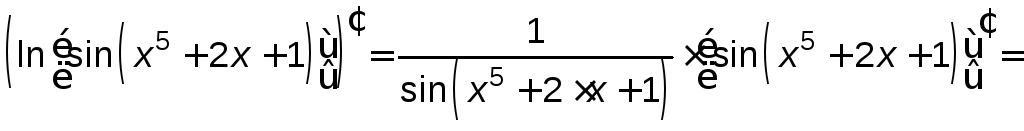
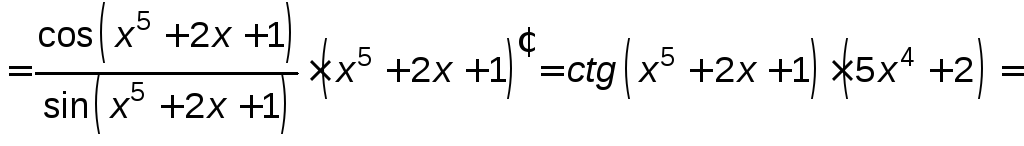
![]() .
.
3. Дифференциал функции
Пусть
функция в точке x0
имеет производную. По определению
производной (п.1.1)
![]() ,
поэтому по свойствам предела можно
записать
,
поэтому по свойствам предела можно
записать![]() ,
где
,
где![]() –
бесконечно малая при
–
бесконечно малая при![]() .
Отсюда
.
Отсюда
![]() .
(3.1)
.
(3.1)
При
![]() второе слагаемое в равенстве (3.1) является
бесконечно малой высшего порядка, по
сравнению с
второе слагаемое в равенстве (3.1) является
бесконечно малой высшего порядка, по
сравнению с![]() :
:![]() ,
поэтому
,
поэтому
![]() и
и
![]() – эквивалентные бесконечно малые (при
– эквивалентные бесконечно малые (при![]() (x0)
(x0)![]() 0).
0).
Таким
образом, приращение функции
![]() состоит из двух слагаемых, первое из
которых
состоит из двух слагаемых, первое из
которых![]() являетсяглавной
частью
приращения
являетсяглавной
частью
приращения
![]() ,
линейной относительно
,
линейной относительно![]() (при
(при
![]() ).
).
Дифференциалом
функции
![]() в точке
в точке![]() называется главная часть приращения
функции и обозначается:
называется главная часть приращения
функции и обозначается:![]() или
или![]() .
Следовательно,
.
Следовательно,
![]() .
(3.2)
.
(3.2)
Пример
3.1.
Найти дифференциал и приращение функции
![]() при: 1) произвольных
при: 1) произвольных![]() и
и![]() ;
2)
;
2)![]() ,
,![]() .
.
Решение.
1)![]() ,
,![]() .
.
2)
Если
![]() ,
,![]() ,
то
,
то![]() ;
;![]()
Запишем равенство (3.1) в виде:
![]() (3.3)
(3.3)
Приращение
![]() отличается от дифференциала
отличается от дифференциала![]() на бесконечно малую высшего порядка,
по сравнению с
на бесконечно малую высшего порядка,
по сравнению с![]() ,
поэтому в приближенных вычислениях
пользуются приближенным равенством
,
поэтому в приближенных вычислениях
пользуются приближенным равенством![]() ,
если
,
если![]() достаточно мало.
достаточно мало.
Учитывая,
что
![]() ,
получаем приближенную формулу:
,
получаем приближенную формулу:
![]() (3.4)
(3.4)
Пример
3.2.
Вычислить приближенно
![]() .
.
Решение.
Рассмотрим: функцию
![]() ,
при
,
при![]() ,
,![]() .
Тогда
.
Тогда![]() .
.
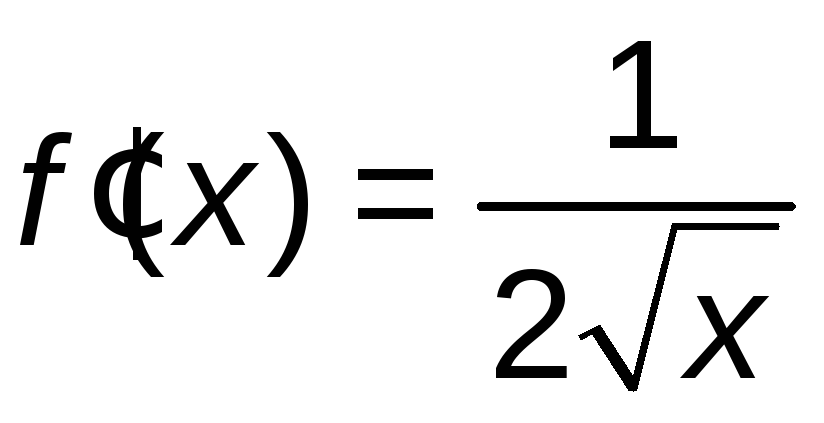 ,
,
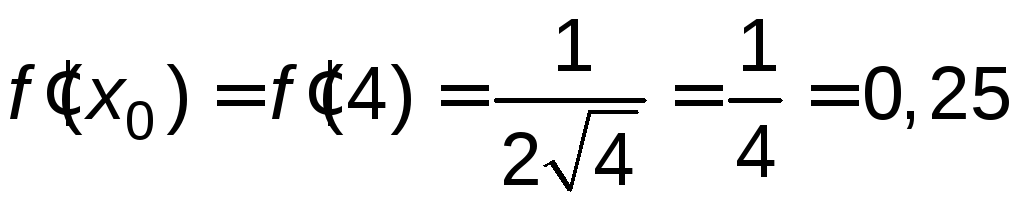
![]() .
.
Используя формулу (3.4), получим:
Значит
![]()
4. Дифференцирование обратной функции, функций заданных неявно, параметрически. Логарифмическое дифференцирование
4.1. Дифференцирование обратной функции
Введем правило для нахождения производной обратной функции.
Теорема.
Пусть функция
![]() определена на промежуткеХ,
непрерывна, монотонна (возрастает или
убывает) и дифференцируема на Х.
Если ее производная
определена на промежуткеХ,
непрерывна, монотонна (возрастает или
убывает) и дифференцируема на Х.
Если ее производная
![]() в точке
в точке![]() не равна нулю, тообратная
функция
не равна нулю, тообратная
функция
![]() имеет производную
имеет производную![]() в точке
в точке![]() ,
причем
,
причем
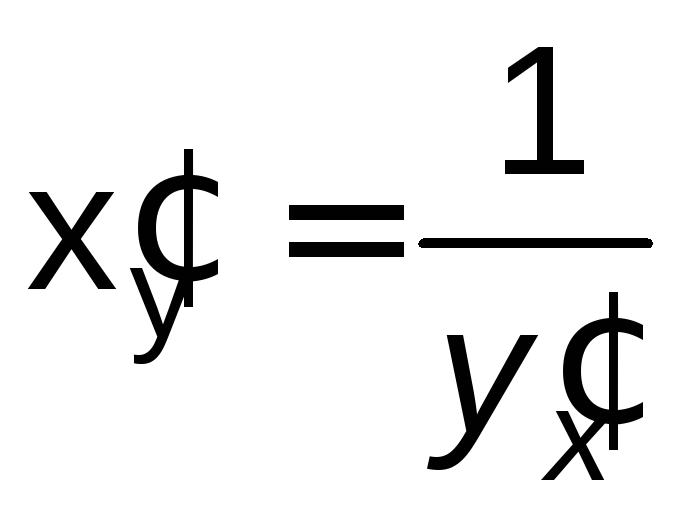 (4.1)
(4.1)
Доказательство.
Функция
![]() определена, непрерывна и монотонна на
промежуткеХ,
тогда она имеет обратную функцию
определена, непрерывна и монотонна на
промежуткеХ,
тогда она имеет обратную функцию
![]() ,
определенную, непрерывную и монотонную
на промежуткеY.
,
определенную, непрерывную и монотонную
на промежуткеY.
Если
значение аргумента
![]() получает приращение
получает приращение![]() ,
отличное от нуля, то в силу монотонности
функции
,
отличное от нуля, то в силу монотонности
функции![]() функция
функция![]() получает приращение
получает приращение![]() и
и![]() .
В силу непрерывности функции
.
В силу непрерывности функции![]() :
:![]() .
.
Следовательно,
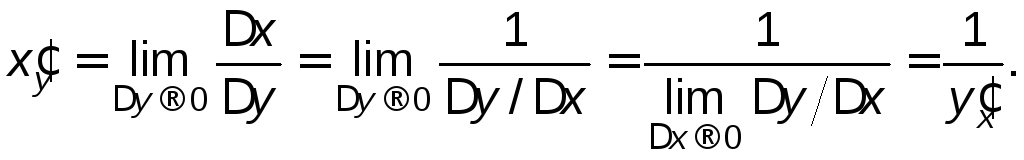
Итак,
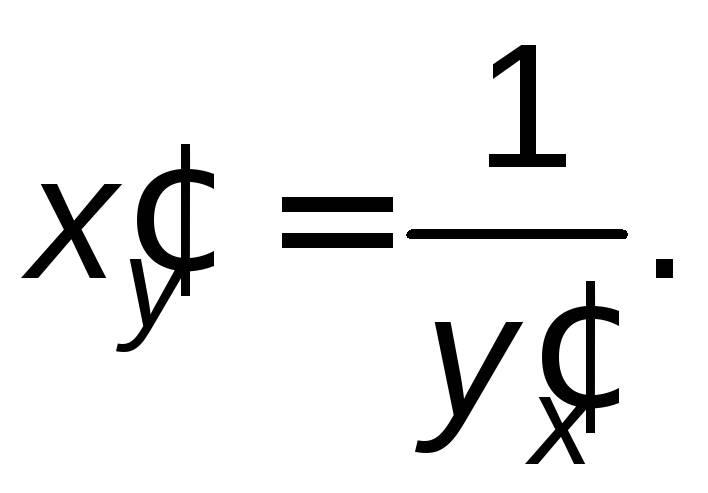
Теорема доказана.
Пример
4.1.
Если
![]() ,
,![]() ,
то функции
,
то функции![]() ,
,![]() являются взаимно обратными, причем
являются взаимно обратными, причем![]() .
Если
.
Если![]() (при этом
(при этом![]() ),
то
),
то![]() ,
поэтому
,
поэтому![]() .
.
По
формуле (4.1) имеем:
 тогда
тогда
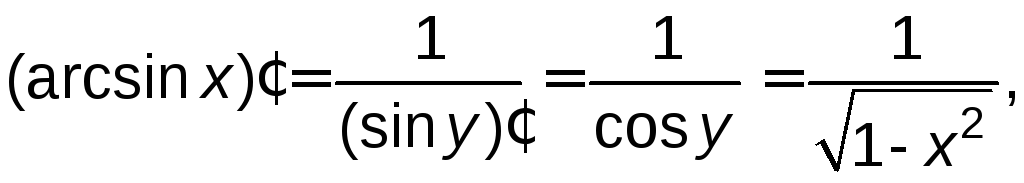 (
(![]() ).
).
