Файловый архив студентов. Файловый архив студентов.
1261 вуз, 4614 предмет.
/ Регистрация
FAQ Обратная связь Вопросы и предложения
Добавил:
Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.
Вуз:
Казахский национальный университет им. аль-Фараби
Предмет:
[НЕСОРТИРОВАННОЕ]
Файл:

теорет.механика

.pdf
Скачиваний:
140
Добавлен:
24.03.2015
Размер:
1.02 Mб
Скачать
☆

Б а қ ы л а у с ұ р а қ т ар ы

1.Орнықты тепе-теңдік күй дегеніміз не?

2.Аз тербелістер дегеніміз не?

3.Еркін тербеліс анықтамасы.

4.Аз тербеліс жасаған болса жүйенің потенциалдық энергиясы?

5.Гармониялық тербеліс дегеніміз не?

17 Мəжбүр тербелістер

Жүйеге сырттан айнымалы күш əсер еркенде ол мəжб р тербеліс жасайды. Тербелісті аз деп қарастырғандықтан, осы жүйеге əсер етеін күшті де əлсіз деп алуға болады. Себебі бұл күштің əсері жоғары болса x – ауытқуы үлкен болып кетер еді де, тербеліс аз тербеліс бола алмайтын еді. Осы жағдайда

жүйенің меншікті U (x) = kx2 – потенциалдық энергиясынан басқа қосымша

2

сырттан əсер ететін өрістің U c (x, t ) энергиясы да бар болады. x – координатасына байланысты өзгерісі аз болғандықтан мұны да жіктейміз:

U c (x, t ) = U c

(0, t ) +

dU (x, t )

 

x=0 × x + ××× = U c (0, t ) - F (t )× x

(1)

 

 

 

 

 

 

 

 

 

dx

 

 

 

 

 

 

 

 

 

 

 

 

dU (x, t )

 

x=0 × = -F (t )

(2)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

dx

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

U c (0,t ) тек уақыттың функциясы болғандықтан, оны уақыттың толық

туындысы ретінде Лагранж функциясынан алып тастаймыз:

 

 

L =

mxɺ2

 

-

kx 2

+ x × F (t ) + ×××

(3)

 

 

 

 

 

2

 

 

 

2

 

 

 

 

 

 

Қозғалыс теңдеуі

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ɺɺ

+ ω

2

x

=

F (t )

.

(4)

 

 

 

 

 

 

 

 

 

 

x

 

 

 

 

m

Бұл тұрақты коэффициенттері бар біртекті емес сызықты дифференциалды теңдеу. Осы қарастырып отырған мəжбүр тербелістің қозғалыс теңдеуінің шешімі мынадай қосындыны береді:

 

 

x = x0 + xд .

 

Мұндағы

 

x0

–

біртекті теңдеудің жалпы шешімі,

 

xд

–

біртекті емес теңдеудің дара (дербес) интегралы.

 

 

 

x0 = A cos(ωt + α )

(5)

81

ɺxɺ+ ω 2 x = F (t ) түрлендірсек:

m

ɺxɺ+ iωxɺ − iωxɺ + ω 2 x = F (t ) m

d (xɺ + iωx) − iω(xɺ + iωx) = F (t ) dt m

белгілеу енгіземіз:

y = xɺ + iωx

Сонымен

yɺ − iωy = F (t ) m

Осының біртекті шешімі

y0 = Aeiωt

(6)

(7)

(8)

(9)

A = A(t ) толық шешімін табу керек. Ол үшін тұрақтыларды вариациялау əдісін қолданамыз. Яғни тұрақтыларды уақыттың функциясы ретінде аламыз:

y = A(t )eiωt

yɺ = A(t )iωeiωt + Aɺ(t )eiωt

Орнына қойғанда

Aɺ(t ) = F (t ) e−iωt m

Сонымен

A(t ) = ∫ F (t ) e−iωt dt + c m

 

F (t )

 

 

y = eiωt A(t ) = eiωt ∫

 

 

e

−iωt dt + c

 

 

 

m

 

 

y = xɺ + iωx = G(t ) белгілесек, жалпы жағдайдағы шешімі:

(11)

(12)

(13)

(14)

82

 

iωt

 

iωt

 

−iωt

′

 

xд = e

B(t ) = e

{∫G(t )e

dt + c }

(15)

 

 

 

Енді F (t ) – айқын түрі берілген жəне ол периодты гармониялық функция түрінде берілген жағдайды қарастырамыз.

ɺxɺ+ ω 2 x =

F0

cos(γt + β )

(16)

 

 

 

 

m

 

түрінде берілген болса, оның шешімі:

 

x = x0 + xд , ал x0 = A cos(ωt + α ), xд = B cos(γt + β )

(17)

B =

 

 

F0

 

m(ω 2γ 2 )

;

 

(18)

Орнына қойғанда:

 

 

 

 

 

F0

 

x = A cos(ωt + α ) +

m(ω 2γ 2 )

cos(γt + β )

(19)

Сонымен сырттан периодты күш əсер еткенде жүйе жүйенің меншікті ω жиілігі жəне мəжбүрлеуші күштің жиілігі γ болатын екі тербелістің қосындысынан тұратын қозғалысқа келеді.

Ал бірақ ω = γ болғанда, яғни резонанс кезінде бұл (19) теңдеуді қолдана алмаймыз. (16) теңдеуді қайтадан жазамыз:

ɺxɺ+ ω 2 x = F0 cos(γt + β ) m

Дара шешімін былай іздейміз:

xд

= Bt sin(ωt + β )

(20)

Бірінші ретті жəне екінші ретті туындыларын алып, оларды (16) қойғанда:

 

 

B =

 

F0

 

(21)

 

 

2mω

 

 

 

 

 

Сонымен дара шешімі

 

 

 

 

 

 

xд =

F0

 

t sin(ωt + β )

(22)

2mω

 

 

 

 

 

Ал жалпы шешімі

83

x = A cos (ω t + α ) +

F0

 

2 m ω t sin (ω t + β )

(23)

Резонанс кезінде амплитуда осылай шексіз өсе береді. Осындай тербеліс жасайтын жүйенің энергиясы

E =

m

ɺ2

+ ω

2

x

2

) =

m

 

ξ

 

2

(24)

 

 

 

 

 

 

 

 

 

2

(x

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Мұндағы

 

 

 

 

 

 

 

 

∞

 

2

 

 

 

 

 

 

 

 

 

 

ξ (∞)

 

2

=

1

 

∫ F (t )e−iωt dt

 

(25)

 

 

 

 

 

 

 

m

2

 

 

 

 

 

 

 

 

 

−∞

 

 

 

 

 

 

 

 

 

 

 

 

Сонымен энергияға арналған өрнекті қайтадан жазатын болсақ:

 

1

 

∞

 

2

 

 

 

E =

 

∫ F (t )e−iωt dt

 

(26)

2m

 

 

−∞

 

 

Егер сыртқы күш жүйеге өте аз уақыт аралығында əсер етті деп есептесек, e−iωt ≈ 1, сонда:

E =

Б а қ ы л а у с ұ р а қ т ар ы

1

 

∞

 

2

 

 

∫ F (t )dt

.

(27)

 

2m

−∞

 

 

 

1.Мəжбүр тербеліс дегеніміз не?

2.Тейлор қатарына жіктеу.

3.Сипаттаушы теңдеу.

4.Мəжбүр тербеліс потенциалдық энергиясы.

5.Резонанс.

18 Өшетін тербелістер

Біз тербелістерді қарастырғанда дененің қозғалысын бос кеңістікте немесе денеге ортаның əсері елеусіз болатын жағдайларды қарастырдық. Негізінде қозғалыс болған ортада осы ортаның қозғалысты тоқтатуға бағытталған əсер күші пайда болады да, қозғалыстағы дененің энергиясы бірте-бірте жылуға айналады немесе осындай қозғалыс тек қана механикалық процесс қана емес, ортаның жəне дененің жылулық күйін ескеруді қажет ететін күрделі құбылыс болып табылады. Сонымен ортадағы дененің қозғалыс теңдеуі механикадағы қозғалыс теңдеуінен өзгеше болады.

Сонда да ортадағы дененің қозғалысы туралы теңдеуде осы ортаның күйін сипаттайтын қосымша мүшені ескерсек, қозғалыс теңдеуін жазуға болады. Осы

84

қосымша мүшелерге, мысалы, ортаның ішкі диссипативті қасиетін сипаттайтын тербеліс жиілігі жатады. Əдетте, бұл тербеліс жиілігі тербелістегі дененің меншікті жиілігінен аз болады. Осы жағдай орындалғанда тербелістегі денеге тек жылдамдыққа тəуелді үйкеліс күші əсер етеді:

 

 

 

 

 

 

fйк= -α

 

x

 

 

 

 

 

(1)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ɺ

 

 

 

 

 

 

Негізінде α –

оң таңбалы,

«–»

таңбасы күштің

 

жылдамдыққа

қарсы

бағытталғанын көрсетеді. Сонымен қозғалыс теңдеуі:

 

 

 

 

 

 

 

 

 

mxɺ = −kx − αxɺ

 

 

 

(2)

 

 

 

 

 

 

 

k

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

= ω0

;

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

m

 

 

 

 

 

 

 

 

 

 

(3)

 

 

 

 

 

 

 

α

= 2λ.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

m

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ɺɺ

+

k

+

α

ɺ

= 0

 

 

 

 

(4)

 

 

 

 

 

 

x

 

 

 

 

 

 

 

 

 

x

 

 

m

x

 

 

 

 

 

 

 

 

 

 

 

m

 

 

 

 

 

 

 

 

 

 

белгілеулерін енгіземіз.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ɺɺ

 

 

2

 

 

 

ɺ

 

 

 

 

 

 

(5)

 

 

 

 

x

+ ω0 x

+ 2λx = 0

 

 

 

ω0 –

үйкеліс жоқ

кездегі

жүйенің

еркін тербелісінің жиілігі, λ

–

.шу

коэффициенті деп аталады.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тұрақты коэффициенттері бар сызықты теңдеулерді шешудің жалпы

ережесін пайдаланып:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x = e rt

 

 

 

 

 

 

 

 

(6)

деп

аламыз жəне

r үшін

сипаттаушы теңдеуді іздейміз. xɺ = re rt,

ɺxɺ= r 2ert

болғанда,

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

r2ert+2 λre rt+ω 02ert=0

 

 

 

 

 

 

 

 

 

 

r2+2 λr + ω 02=0

 

 

 

 

Осы теңдеуді шешеміз. Шешімі:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x = c er1t + c

2

er2t

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

(7)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

= −

2λ ±

 

 

 

 

 

 

 

 

 

 

 

 

4λ2 − 4ω02

 

 

= −λ ±

 

 

 

 

 

 

 

r

 

 

λ2 − ω

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

1,2

 

 

 

 

2

 

 

 

 

 

 

 

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

85

r

= −λ −

λ2

− ω 2

 

 

1

 

 

 

0

 

 

 

= −λ +

 

 

 

 

 

r

 

λ2

− ω 2

(8)

2

 

 

 

0

 

 

шешімінің түрі 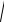λ2 − ω02 – қатынасына байланысты.

1)λ<ω0 – түбірден теріс сан шығып, мəні комплексті болады.

2)λ>ω0 – оң болады.

3)

λ =ω0 eiα = cosα + i sin α гармониялық функция болады да,

функция тербелісті сипаттайды.

x = αe−λt cos(ωt + α )

x = c e−λt

cosωt + c e−λt sin ωt = e−λt (c cosωt + c

sin ωt ) = ae−λt cos(ωt + α )

(9)

1

 

 

 

 

2

 

 

 

 

 

 

 

1

 

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

a =

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

c 2

+ c

2

 

 

 

 

 

 

 

 

(10)

 

 

 

 

 

 

 

 

 

 

 

 

 

1

 

2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x = ae−λt cos(ωt + α )

 

 

 

 

 

 

 

(11)

Осындай түрдегі тербелісті .шетін тербеліс деп аталады.

 

 

 

 

2)Енді λ>ω0 тербелісті былай анықтайды:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

− (λ −

 

 

 

)t

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

t

 

 

t

 

 

λ

−ω

 

 

 

 

 

 

 

 

t

 

 

 

 

 

x = c

e r1

 

+ c

2

e r2

= c

e

 

 

 

0

 

+ c

2

e −(λ +

λ

−ω0

) = c

e −α1t

+ c

2

e −α 2 t

(12)

1

 

 

 

 

1

 

 

 

 

 

 

 

 

 

 

 

 

1

 

 

 

 

α 1,α 2 – оң сандар.

Яғни екеуі де экспоненциалды кемитін функциялар. Яғни периодты емес түрде өшеді. Бұл апериодты өшетін қозғалыстың бір түрі.

1)с1, с2 - оң

2)с1 – оң

с2 – теріс 3) λ = ω0 жағдай

r = −λ шешімді былай іздейміз:

x = (c

1

+ c

2

)e −λt

(13)

 

 

 

 

Бұл да өшетін апериодты тербелістің маңызды жағдайы болады. Бұл жағдайда да қозғалыс тербелістік сипатта болмайды.

Б а қ ы л а у с ұ р а қ т ар ы

1.Өшетін тербеліс дегеніміз не?

2.Апериодты тербеліс дегеніміз не?

3.Өшу коэффициенті.

4.Үйкеліс күші.

5.Біртекті емес дифференциалдық теңдеу.

86

19 Үйкеліс бар кездегі мəжбүр тербелістер

Үйкеліс бар кездегі мəжбүр тербелістердің қозғалыс теңдеуін жазу үшін:

 

 

 

mx = −kx − αx

 

 

 

 

 

 

 

 

 

 

 

(1)

 

 

 

 

ɺɺ

 

ɺ

 

 

 

 

 

 

 

 

 

 

 

 

теңдеуіне сыртқы күш f0 cosγt -ны қосып жазамыз.

 

 

 

 

 

 

 

 

 

 

 

ɺxɺ+ 2λxɺ + ω02 x =

f0

cos γt

 

 

 

 

 

 

 

 

 

(2)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

m

 

 

 

 

 

 

 

 

 

 

 

 

Біртекті теңдеудің шешімі:

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

x = c1 e r1t + c2 e r2 t

 

 

 

 

 

 

 

 

 

 

(3)

Ал дербес шешімі :

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

xд

= β1 cos γt + β 2 sin γt

 

 

 

 

 

 

 

 

 

(4)

 

 

xɺд = −β1γ sin γt + β 2γ cos γt

 

 

 

 

 

 

 

 

 

 

 

ɺxɺ

= −β γ 2

cos γt − β

2

γ 2

sin γt

 

 

 

 

 

 

 

 

 

 

д

 

1

 

 

 

 

 

 

 

 

 

 

 

 

 

 

орнына қоямыз

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

− β γ 2 cosγt − β γ 2 sin γt + 2λ(− β γ sin γt + β γ cosγt ) + ω2

(β cosγt + β

2

sin γt ) =

f0

cosγt

 

1

2

 

1

 

2

 

 

 

 

0

 

1

 

 

 

m

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

cosγt(− β γ 2

+ 2λβ γ + ω 2

β )+ sin γt(− β γ 2 − 2λβ γ + ω2

β )=

f0

cosγt

 

 

 

 

 

 

 

1

2

0

1

2

 

 

 

1

0

 

 

m

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

β1 (ω02 − γ 2 )+ 2λγβ2 = f0 m

β2 (ω02 − γ 2 )− 2λγβ2 = 0

(5)

β 2

=

2λγβ1

 

(6)

ω02 − γ 2

 

 

 

(5)-ке қойғанда:

β1 (ω02 − γ 2 )+ 2λγ

2λγβ1

 

=

f0

(7)

(ω02 − γ 2 )

m

 

 

 

87

 

 

 

 

 

 

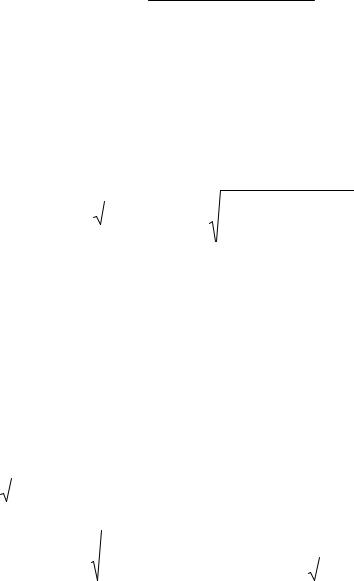
f (ω 2 − γ 2 )

 

 

β1 = m((ω 2 − γ

2 )2 + 4λ2γ 2 )

 

 

 

 

 

0

 

0

 

 

 

 

 

 

0

 

 

 

β 2

=

 

2λγ

 

 

f

0 (ω02 − γ 2 )

 

ω 2 − γ 2

 

m((ω 2

− γ 2 )+ 4λ2γ 2 )

 

 

 

 

 

 

0

 

 

 

0

 

 

2λγf

β2 = m((ω02 − γ 2 )2 0+ 4λ2γ 2 )

Сонымен, теңдеудің дербес шешімі:

xg = β1 cos γt + β2 sin γt = b cos(γt + β )

ендеше:

 

 

 

 

 

f0

1

 

b =

2

+ β

2

=

 

β1

 

 

 

 

 

 

,

2

m

 

(ω02 − γ 2 )2 + 4λ2γ 2

 

 

 

tgβ =

 

2λγ

 

 

 

 

 

.

 

 

 

 

γ 2 − ω 2

 

 

 

 

 

 

 

0

 

 

Толық шешім

x = c1er1t + c2 er2t + b cos(γt + β )

(8)

(9)

(10)

(11)

(12)

Яғни біршама уақыт өткен соң алдыңғы екі мүше шексіз азға айналады.

Яғни біртекті мүшелері нөлге айналады.

 

 

 

 

 

 

 

 

 

γ = ω 2

=

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

ω 2

− 2λ2

орнына қоямыз:

 

 

 

 

 

 

 

 

 

0

 

0

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

b =

f0

1

 

=

f0

1

 

;

(13)

 

 

 

m

 

 

(ω02 − γ 2 )2 + 4λ2γ 2

 

m

 

2λ

 

 

 

 

 

 

 

 

ω02 − λ2

Үйкеліс жағдайында да бұл резонанс та шексіздікке айналмайды.

20 Ангармониялық тербелістер

Жүйені бастапқы орнықты қалпына келтіруге əсер ететін күшті алдыңғы тақырыптарда қатарға жіктеген болатынбыз:

f = -kx + αx2 + βx3 + ×××

(1)

88

Осындағы бірінші мүше серпімді күш болып, осы күштің əсерінен жүйе гармониялық тербеліс жасайды деп айтқан болатынбыз. Енді осы қатардағы екінші мүшені ескеріп, қозғалыс теңдеуін жазсақ, былай болады:

ɺɺ

2

2

.

(2)

x

+ ω0 x = αx

Осы бейсызық теңдеу ангармониялы вибраторды

теңдеуі болып

табылады.

Осы теңдеуді шешу үшін аз параметрлері бойынша жіктеу тəсілін қолданамыз. Аз параметр ретінде бастапқы ауытқу немесе бастапқы жылдамдықтың мəнін алады.

Аз параметрдің мəнінің екінші дəрежесіне дейінгі дəлдікпен алғанда:

 

x = x1 + x2 ,

(3)

мұндағы х1 – аз параметрдің бірінші реті, х2 – екінші ретті мүшелері. (3)-ті (2)-ге қойып, бірдей параметрлерді теңестіріп мына теңдеуді аламыз:

ɺxɺ2

+ ω2 x

= 0;

(4)

 

1

0

1

 

 

ɺxɺ2

+ ω2 x

2

= αx2 .

(5)

2

 

0

1

 

(4)-шешімі гармониялық тербеліс болады.

x1 = c cos(ω0t + ϕ ),

(6)

(φ=0) болу керек. Бастапқы шарттарын бергенде:

x

 

t =0 = a; xɺ

 

t =0 = 0;

(7)

 

 

(6) теңдеуінің шешімі былай болады:

x1 = a cos ω0t

(8)

Амплитуда мəні a -ны жіктеу жүргізуге арналған аз параметр ретінде алуға болады.

Енді (8)-ді (5) теңдеудің оң жағына қоямыз:

xɺ2 + ω02 x2 = αa2 cos2 ω0t

cos2 α = 1 (1 + cos 2α ) формуласын қолданып жазамыз: 2

89

ɺxɺ2 + ω02 x2 = αa 2 (1 + cos 2ω0t ) 2

Осы теңдеудің шешімін былай іздейміз:

x2 = c1 + c2 cos 2ω0 t ,

жəне дербес шешімі:

 

 

 

 

 

 

 

 

x = αa2

− αa2

cos 2ω t .

 

 

2

2ω2

6ω 2

 

0

 

 

 

 

 

 

 

 

 

 

 

0

 

0

 

 

 

 

(9) теңдеудің шешімі:

 

 

 

 

 

 

 

 

x = Acosω0t + B sin ω0t + xд

x = Acosω t + B sinω t + αa2

− αa2

cos 2ω t

0

 

0

 

2ω 2

6ω 2

0

 

 

 

 

 

 

 

 

 

 

0

 

0

 

(9)

(10)

(11)

(11)

(7) шартты қанағаттандыра отырып, A жəне B тұрақтыларының мəнін табамыз:

 

 

1 αa

αa2

 

1

 

x = a 1

−

 

 

cosω0t +

 

1

−

 

cos 2ω0t

2

2

3

 

 

3 ω0

 

2ω0

 

 

 

Сонымен осы теңдеудің шешімінен көріп тұрғанымыздай,

тербелістің жиілігі 2-есеге артты, бастапқы тыныштық қалпынан ауытқу пайда болды.

(12)

гармониялық

αa2

2ω02 шамаға

Б а қ ы л а у с ұ р а қ т ар ы

1.Ангармониялық тербеліс дегеніміз не?

2.Аз параметрді қолдану.

3.Ангармониялық вибратор.

4.Үйкеліс күші.

5.Үйкеліс бар кездегі мəжбүр тербелістер.

90

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
Помощь Обратная связь Вопросы и предложения Пользовательское соглашение Политика конфиденциальности