
теорет.механика
.pdfI1 = A1i A1k Iik , |
|
|
I 2 |
= A2i A2k I ik , |
|
I 3 |
= A3i A3k I ik . |
(11) |
Инерция тензоры диагоналдық түрге келетін x′, y′, z′ – координаттар жүйесінің осьтерін инерция тензорының бас остері деп атайды.
Жаңа координаттық осьтер арқылы кинетикалық энергия былай жазылады:
T = |
1 |
(I Ω2 + I |
Ω2 |
+ I |
Ω2 ), |
(12) |
||
|
||||||||
2 |
1 |
1 |
2 |
2 |
3 |
3 |
|
|
|
|
|
|
|
|
|
||
Бас осьтердегі инерция моменттері инерцияның бас моменттері деп |
||||||||
аталады. Олар I1 , I 2 , I 3 – деп белгіленген. |
|
|
|
|
|
|||
I1 + I 2 |
³ ∫ ρ (x¢2 |
+ y¢2 )dV = I 3 , |
(13) |
|||||
Яғни, үш бас инерция моменттерінің біреуі, қалған моменттердің қосындысынан үлкен болмайды. Осындай қатты денені жазы $ршы деп атайды. Бас инерция моменттерінің мəндері əр түрлі болған жағдайда денелер ассимметриялы $ршы деп аталады. Егер де бас инерция моменттерінің екеуі бір-біріне тең болса, ол I1=I2≠I3 — симметриялы $ршы деп аталады. – жазықтығында бас осьтердің бағытын қалауымызша ала аламыз. Егер бас инерция моменттерінің үшеуі де бір-біріне сəйкес болса, ол дене шар $ршы болады. Бұл жағдайда барлық үш бас инерция осьтерін таңдауымыз бойынша ала аламыз; яғни өзара перпендикуляр кез-келген үш осьті де алуға болады. Бас инерция моментінің екеуі бір-біріне тең I1=I2 I3=0, үшіншісі нөлге тең болған жағдайда бұл дене сызы ты $ршы немесе ротатор болып табылады. Ротатордың тек екі ғана айналу еркіндік дəрежесі бар, яғни тек қана x′ жəне y′ осьтерінің маңында айналады, ал түзудің өз маңында айналуы жағдайы қарастырылмайды.
Инерция тензорын есептеудің тағы бір түрін қарастырамыз. Біздің есептеген қарастырған инерция тензоры координаттық осьтері инерция центрінде орналасқан дене үшін қарастырылды. Осыған ұқсас кез-келген бір O′ оське қатысты алынған инерция тензорын есептесек:
|
|
|
|
|
|
|
Iik/ |
= ∑ m(xl/ 2δik |
− xi/ xk/ ), |
(14) |
|
|
|
|
|
тең болса: |
|
– |
массалар |
центрі мен |
осьтің арақашықтығы |
|
|
|||||||||
|
|
OO¢ |
|
= a |
r |
|||||
векторлық түрде |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
r ′ = r + a , |
(15) |
|
немесе |
|
|
|
|
|
|
|
|
||
101
|
|
|
|
|
x / |
= x |
/ |
+ a |
, |
|
|||
|
|
|
|
|
i |
|
|
|
i |
|
|
||
O нүктесі инерция центрінде орналасқан, яғни |
|
||||||||||||
|
|
∑ mr = 0 , R = |
∑ mr = 0 , |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
∑m |
|
||
|
|
|
Iik/ = Iik + μ(a2δik − ai ak ). |
′ |
|||||||||
Яғни осы формуланы пайдаланып, |
ізделініп отырған |
||||||||||||
Iik |
|||||||||||||
болады. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
r ′ = r + a |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||||
Iik/ = ∑ m(xl/ 2δik |
− xi/ xk/ ) = |
x/ |
= x + a |
|
= |
∑ m{xl/ 2δik + ai/ 2δik |
|||||||
i |
i |
|
i |
|
|||||||||
x/ |
= x |
|
+ a |
|
|||||||||
|
|
k |
k |
|
|
|
|
|
|||||
|
|
k |
|
|
|
|
|
|
|
|
|||
|
|
∑ mr = 0 |
|
|
|
|
|
|
|||||
(16)
(17)
(18)
–тензорын есептеуге
+2ai xiδik − (xi + ai )(xk + ak )}=
= ∑ m{xi/ 2 δ ik + ai/ 2 δ ik − xi xk − xi ak − xk ai − ai ak }= I ik + μ{ai2 δ ik − ai ak }, (19)
мұндағы Iik = ∑ m{xl/ 2δik − xi xk }, ал, ∑ m = μ .
Б а қ ы л а у с ұ р а қ т ар ы
1.Инерция тензоры.
2.Инерцияның бас осьтері.
3.Қатты дененің Лагранж функциясы.
4.Жазық ұршық.
5.Асимметриялы ұршық.
24 Қатты дененің импульс моменті
Жүйенің импульс моментінің шамасы оны қай нүктеге қатысты таңдап алғанға байланысты екенін білеміз:
|
|
|
M = ∑ m[rv ]. |
(1) |
|
Қатты дененің орны қозғалыстағы санақ жүйесінде, яғни инерция |
||
центрінде орналасқан |
|
|
|
|
(2) |
M |
= M ′ + [RP] |
|
102
Санақ жүйесінің басы инерция центрінде орналасқан жағдайда дененің моменті M «меншікті моментімен» сəйкес болады да v = V + [Ωr ] өрнегіндегі ілгерімелі қозғалысының жылдамдығы ескерілмейді, яғни [Ωr ] -арқылы
M = ∑ m[r [Ωr ]]= ∑ m{r 2 Ω − r (rΩ)}, |
(3) |
немесе тензорлық белгілеулер арқылы жазатын болсақ:
M i = ∑ m(xl2 Ω i − xi xk Ω k ) = |
|
Ω i = Ω k δ ik |
|
= Ω k ∑ m{xl2 δ ik − xi xk }, |
(4) |
|
|
мұндағы
∑ m{xl2 δ ik − xi xk }= I ik , |
(5) |
яғни инерция тензоры екенін ескерсек:
M i = I ik Ω k , |
(6) |
Егерде x′, y′, z′ - бас осьтері дененің бас инерция осьтерімен сəйкес болса:
M 1 |
= I1 Ω1 |
|
M 2 |
= I 2 Ω 2 |
|
M 3 |
= I 3 Ω 3 |
(7) |
I1 = I 2 = I 3 бас инерция моменттері тең болатын шар ұршық үшін |
|
|
M = IΩ , |
(8) |
|
момент векторы бұрыштық жылдамдыққа пропорционал жəне онымен бағыттас болады. Сырттан күштер əсер етпейтін жəне дененің ілгерімелі қозғалысын ескермеуге болатын немесе дененің еркін айналмалы қозғалысын қарастырамыз. Барлық тұйық жүйелер сияқты еркін айналып тұрған дененің
импульс |
моменті тұрақты болады. |
I1 = I 2 = I 3 |
болатын шар ұршық үшін |
|
|
|
|
|
|
M =const шарты Ω =const шартына əкеліп соғады. Яғни, жалпы жағдайда еркін |
||||
айналып тұрған шар ұршығы, тұрақты осьті бірқалыпты айналып тұрады. |
||||
|
|
(I1 = I2 ; I3 |
|
|
Сол сияқты ротатор жағдайында |
= 0), M = IΩ болады, сонымен |
|||
|
|
|
|
болады. Сондықтан |
қатар Ω |
векторы ротатордың осіне перпендикуляр |
|||
ротатордың еркін айналуы, осы жазықтыққа перпендикуляр бағыттың маңында бірқалыпты айналуы болып табылады.
103
′ |
′ |
инерцияның бас осьтерін қалауымызша ала-алғандықтан, y |
′ |
осін M |
||
x , y |
|
|
||||
тұрақты векторы |
жəне z′ осінің лездік орнымен сипатталатын жазықтыққа |
|||||
перпендикуляр етіп аламыз, сонда M 2 = 0 , ал |
|
|
||||
|
|
|
M 1 |
= I1 Ω1 , |
|
|
|
|
|
M 2 |
= I 2 Ω 2 , |
|
|
|
|
|
M 3 |
= I 3 Ω 3 , |
|
(9) |
формуласынан Ω2 |
= 0 болады. Яғни M , Ω векторлары жəне ұршықтың осі |
|||||
əрбір уақыт моментінде бір жазықтықта жатады. |
|
|
||||
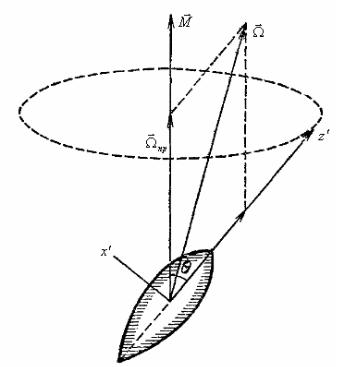
28 – сурет
Бірақ v = [Ωr ] барлық нүктелердің жылдамдықтары əрбір уақыт моментінде берілген жазықтыққа перпендикуляр. Басқаша айтқанда, ұршықтың осі дөңгелек конусты (ұршықтың бірқалыпты прецессиясы деп аталатын) сыза отырып M векторының маңында бірқалыпты айналады. Прецессияға қоса ұршық өз осінің маңында бірқалыпты айналады. Ұршықтың өз осінен айналуының бұрыштық жылдамдығы Ω векторының Ω3 проекциясы болып табылады:
Ω3 |
= |
M 3 |
= |
M |
cosθ |
(10) |
I3 |
|
|||||
|
|
|
I3 |
|
||
104
Прецессия жылдамдығы Ωпр табу үшін Ω векторын параллелограмм
ережесі бойынша z′ жəне M құраушыларына жіктеу қажет. |
|
|||||||
sin θ × Wпр = W1 , |
(11) |
|||||||
Ω1 |
= |
M1 |
= |
M sinθ |
, |
(12) |
||
I1 |
|
|
|
|||||
|
|
|
|
I1 |
|
|||
болғандықтан |
Ω |
|
= |
M |
. |
(13) |
||
пр |
|
|||||||
|
|
|
|
I1 |
|
|||
|
|
|
|
|
|
|||
Б а қ ы л а у с ұ р а қ т ар ы
1.Симметриялы ұршық.
2.Шар ұршық.
3.Ротатор.
4.Қатты дененің импульс моменті.
5.Прецессия жылдамдығы.
25 Қатты дененің қозғалыс теңдеулері
Қатты дененің еркіндік дəрежесі алтыға тең болғандықтан, қозғалыс теңдеулер жүйесі алты тəуелсіз теңдеулерден тұруы керек. Оларды дененің импульс жəне момент векторларының уақыт бойынша туындысы ретінде жазуға болады.
Олардың бірінші теңдеулері pɺi = f i деп денені құрайтын бөлшектердің теңдеулерін қосу арқылы табуға болады. Мұндағы pɺi – бөлшектің импульсі, fi
– оған əсер етуші күш. Дененің толық импульсі:
|
|
|
P = ∑ pi |
= μV , |
(1) |
ал денеге əсер етуші күш:
|
= |
|
|
|
F |
∑ fi , |
(2) |
||
|
dP |
|
|
|
|
|
|
= F . |
(3) |
|
|
|
||
dt
Егер U – қатты дененің потенциалдық энергиясы болса:
|
= − |
∂U |
(4) |
F |
. |
||
|
|
∂R |
|
105

R -дененің инерция центрінің координатасы δR қанша өзгерсе, нүктесінің радиус-векторы r -да соншалықты өзгереді, ал энергияның өзгерісі:
δU = ∑ |
∂U |
|
|
∂U |
|
|
||||
δr |
= δR∑ |
|
= −δR∑ fi |
= −FδR |
||||||
|
∂r |
|
|
|
|
∂r |
|
|
|
|
Лагранж теңдеулерін қолданамыз: |
|
|
|
|
|
|||||
|
|
|
d |
|
∂L |
= |
∂L |
, |
|
|
|
|
|
|
|
||||||
|
|
|
dt ∂V |
|
∂R |
|
||||
ал Лагранж функциясы:
дененің əрбір потенциалдық
(5)
(6)
L = |
1 |
μV 2 |
+ |
1 |
I |
|
Ω |
Ω |
|
− U (R), |
(7) |
||||
|
|
|
|
|
|||||||||||
2 |
|
|
2 |
|
ik |
|
i |
|
k |
|
|
||||
|
|
|
∂L |
|
|
|
|
|
|
|
|
|
|||
|
|
|
= μV |
= P , |
(8) |
||||||||||
|
|
|
∂V |
|
|
|
|
|
|
|
|
||||
|
|
∂L |
|
|
|
|
∂U |
|
|
|
|
|
|||
|
|
= − |
|
|
= F . |
(9) |
|||||||||
|
|
∂R |
|
|
|
|
∂R |
|
|
|
|
|
|||
|
|
|
|
d |
= |
|
|
|
(10) |
||||||
|
|
|
|
|
|
|
P |
F |
|
|
|||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
(11) |
|||
|
|
|
|
|
Pɺ = |
F . |
|
|
|
||||||
Енді қозғалыс теңдеулерін импульс моментінің M уақыт бойынша туындысы ретінде аламыз. Ыңғайлы болу үшін санақ жүйесін, берілген уақытта дененің инерция центрі онымен салыстырғанда «тыныштықта» болатындай етіп инерциялды түрде аламыз. Сонымен қатар алынған теңдеулер жүйесі басқа да инерцияларды санақ жүйелерінде Галилейдің салыстырмалық принципі орындалады.
|
d |
|
|
|
|
|
|
|
|
|
M = |
∑[rPi ]= ∑[rɺPi |
]+ ∑[rPɺi |
]. |
|
|
(12) |
||||
dt |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
Таңдап алған санақ жүйесінде |
|
= 0 , |
|
|
болады. |
|
|
|
||
V |
v |
= rɺ |
v |
жəне P = mv |
||||||
векторлары бағыттас болғандықтан |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
∑[rɺPi ]= 0 |
|
|
|
|
|
(13) |
||
|
|
|
106 |
|
|
|
|
|
|
|

|
|
|
|
|
|
|
(14) |
||
|
|
|
|
Pɺ |
|
= f |
i |
|
|
|
|
|
|
i |
|
|
|
|
|
болғандықтан |
|
|
|
|
|
|
|
|
|
|
|
|
dM |
|
|
|
|
|
|
|
|
|
|
|
|
= K . |
|
(15) |
|
|
|
|
|
dt |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
] |
|
|
Себебі |
|
K |
∑[rfi |
(16) |
|||||
|
] – векторы |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
[rfi |
f i к шіні моменті деп аталады. Сондықтан K – |
денеге |
|||||||
əсер ететін барлық күштердің моменттерінің қосындысына тең болып табылады.
Егер координаттар басын a қашықтығында алатын болсақ нүктелердің
жаңа радиус векторлары – r ′ , ескі радиус-вектор r арасындағы байланыс: |
|
|||||
|
|
r = r ′ + a |
|
|
(17) |
|
болса |
|
|
|
|
|
|
|
|
|
′ |
|
] |
(18) |
K = ∑[rfi |
]= ∑[r fi ]+ ∑[afi |
|||||
немесе |
|
|
|
] |
|
|
|
|
|
||||
|
K = K ′ + ∑[aF |
|
(19) |
|||
Осыдан көріп тұрғанымыздай егер F = 0 болса, күш моменті координаттардың бастапқы орнына тəуелді емес. (15) формуласын Лагранж теңдеуі ретінде қарастыруға болады
|
|
|
d |
∂L |
= |
∂L |
|
(20) |
|
|
|
|
|
||||
|
|
|
dt ∂Ω |
|
|
|
||
|
|
|
|
∂ϕ |
|
|||
|
|
|
|
|
|
|
|
|
Лагранж функциясын |
Ω |
|
векторының компоненттері арқылы |
|||||
дифференциалдасақ: |
|
|
|
|
|
|
|
|
|
∂L |
|
= I ik |
×Wk = M i |
(21) |
|||
|
¶Wi |
|||||||
|
|
|
|
|
|
|
||
Дене шексіз аз δϕ бұрышқа бұрылғандағы потенциалдық энергияның өзгерісі
|
|
δU = -∑ fi ×δr = -∑ fi ×[δϕ × r ] = -δϕ ∑[× rfi ]= - Kδϕ , |
(22) |
107
|
|
|
|
|
∂L |
= − |
∂U |
= |
|
|
|
|
|
|
|
|
|
|
|
K . |
|
(23) |
|||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
∂ϕ |
|
∂ϕ |
|
|
|
|
|
|
Егер |
|
|
векторлары өзара перпендикуляр болса (19) формуладағы |
||||||||
|
F |
жəне K |
||||||||||
¢ = 0 айналатын кез-келген a векторын таңдап алуға болатындықтан: |
||||||||||||
K |
||||||||||||
|
|
|
|
|
|
K = [aF ]. |
|
|
(24) |
|||
|
|
|
|
|
|
|
|
|
|
|
күші əсер етеді. |
|
|
Мысалы біртекті күш өрісінде материалдық нүктеге f |
= eE |
||||||||||
|
|
|
– өрісті сипаттайтын тұрақты вектор болса , |
e – |
|
|||||||
Мұндағы |
E |
осы бөлшектің |
||||||||||
берілген өріске қатысты қасиетін сипаттайтын шама. (Біртекті электр өрісінде
E – өрістің кернеулігі, е – бөлшектің заряды). Ал, біртекті ауырлық өрісінде
F - ауырлық күшінің үдеуі g, ал е-бөлшектің массасы m болып табылады.
|
|
F |
= E∑e |
|
|
K = [∑er × E]
∑e ¹ 0 дей отырып, r0 – радиус-векторын енгіземіз:
r = ∑er
0 ∑e
K = [r0 F ]
(25)
(26)
(27)
(28)
Толық күш моментін осылай жазамыз. Сонымен қатты дененің біртекті өрісте қозғалысы кезінде өрістің əсері радиус векторы r0 нүктеге берілген бір
ғана F күшімен сипатталады.
26 Бір нүктесі бекітілген абсолютті қатты дене үшін Эйлердің қозғалыс теңдеулері
Қозғалыс теңдеулері тыныштықтағы координаттар жүйесі үшін жазылған
жəне P жəне M векторларының өзгерісі осындай жүйелерге қатысты алынған:
|
dP |
|
|
|
|
|
|
= F |
|
|
dt |
|
||
|
|
|
|
|
dM |
|
(1) |
||
|
|
|
= K |
|
|
|
|
||
dt
108

Енді қозғалыс теңдеулерін x′,y′,z′ қозғалыстағы координаттар үшін жазып
көреміз. |
dA |
– кез-келген бір |
|
|
|
|
|
|
||
A |
векторының |
тыныштықтағы |
координаттар |
|||||||
dt |
||||||||||
|
|
|
|
|
|
|
|
|
||
жүйесіне |
қатысты |
алғандағы |
уақыт бойынша |
өзгерісі |
деп |
алайық. |
Егер |
|||
|
|
|
|
|
|
|
болса, онда |
|
||
айналмалы |
жүйеге |
қатысты |
A |
векторы өзгермейтін |
оның |
|||||
тыныштықтағы жүйеге қатысты өзгерісі тек айналуға ғана байланысты болады да:
|
(2) |
dA = [WA] |
dt
Cонымен қатар
δr = [δϕ × r ]
δv = [δv × r ] |
(3) |
осы өрнектер кез келген векторлар үшін орындалатыны жоғарыда айтылған
|
d ¢A |
|
|
болатын. (2) өрнектің оң жағына |
– A векторының қозғалыстағы жүйеге |
||
dt |
|||
|
|
қатысты алынған жылдамдығының өзгерісін қосатын болсақ:
|
dA |
|
|
|
|
d ¢A |
|
|
|
|
|
= |
+ [WA]. |
(4) |
|||||||
|
dt |
|
||||||||
|
|
|
|
dt |
|
|
||||
Осы жалпы формуланы пайдаланып (1) өрнекті қайта жазамыз: |
|
|||||||||
|
|
|
|
|
|
|
||||
|
|
d ¢P |
+ [WP]= F |
(5) |
||||||
|
|
|
|
|||||||
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
d ¢M |
+ [WM ]= K |
(6) |
|||||||
|
|
|||||||||
dt
Уақыт бойынша дифференциалдау қозғалыстағы санақ жүйесінде жүргізілгендіктен, теңдеулерді осы осьтердегі проекциялары арқылы жаза аламыз:
d ¢Pdt 1
d ¢Mdt 2
=dP1 ,×××, dt
=dM1 ,..., dt
(7)
(8)
Мұндағы 1,2,3 индекстері x`,y`,z` осьтеріндегі осы теңдеулердің
құраушыларын білдіреді. P = μV алмастырып:
109
|
|
dV |
|
|
+ Ω V − Ω V |
|
= F , |
|
||||||||||||||||||||
μ |
1 |
|
|
|
|
|||||||||||||||||||||||
dt |
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
3 |
|
|
|
|
3 |
|
2 |
|
1 |
|
|
|||||||
|
|
dV |
|
|
+ Ω V − Ω V |
|
= F , |
|
||||||||||||||||||||
μ |
2 |
|
|
|
|
|||||||||||||||||||||||
dt |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
1 |
|
|
|
|
1 |
|
3 |
|
2 |
|
|
||||||||
|
|
dV |
|
|
+ Ω V − Ω V |
|
= F . |
|
||||||||||||||||||||
μ |
|
3 |
|
|
|
(9) |
||||||||||||||||||||||
|
dt |
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
2 |
|
1 |
|
3 |
|
|
|||||||
x`,y`,z` осьтері инерциясының бас осьтері арқылы өтеді дей отыра, (6) |
||||||||||||||||||||||||||||
теңдеуін M 1 = I1 Ω1 , M 2 = I 2 Ω 2 , M 3 = I 3 Ω 3 |
өрнектерін пайдаланып жазамыз: |
|||||||||||||||||||||||||||
I |
|
|
dΩ1 |
|
|
+ (I |
|
|
− I |
|
|
)Ω |
Ω |
|
= K |
, |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
1 |
|
|
dt |
|
|
|
|
3 |
|
|
2 |
|
|
2 |
|
|
3 |
1 |
|
|
|||||||
I |
|
|
dΩ2 |
+ (I |
|
|
− I |
|
)Ω |
|
Ω = K |
, |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
2 |
|
|
dt |
|
|
|
|
|
1 |
|
|
|
3 |
|
|
3 |
|
1 |
2 |
|
|
||||||
I |
|
|
dΩ3 |
|
|
+ (I |
|
|
− I |
)Ω Ω |
|
= K |
. |
(10) |
||||||||||||||
|
|
|
|
dt |
|
|
|
|
|
|||||||||||||||||||
|
3 |
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
|
1 |
|
|
2 |
3 |
|
|
||||||
Осы теңдеулер Эйлер те деулері деп аталады. Еркін айналу кезінде |
K = 0 |
|||||||||||||||||||||||||||
болады да Эйлер теңдеулері былай жазылады: |
|
|
|
|
||||||||||||||||||||||||
|
|
dΩ1 |
+ |
(I3 − I2 ) Ω |
Ω |
|
= 0 , |
|
|
|||||||||||||||||||
|
|
|
3 |
|
|
|||||||||||||||||||||||
|
|
|
dt |
|
|
|
|
|
I1 |
|
|
|
|
2 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
dΩ2 |
+ |
(I1 − I3 ) Ω Ω = 0 , |
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
dt |
|
|
|
|
|
I |
|
|
|
|
|
3 |
|
|
1 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
dΩ3 |
+ |
(I2 − I1 ) Ω Ω |
|
= 0 . |
|
(11) |
||||||||||||||||||||
|
|
|
2 |
|
||||||||||||||||||||||||
|
|
|
dt |
|
|
|
|
|
I |
|
|
|
|
|
1 |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Мысал ретінде симметриялық ұршықтың еркін айналуына осы теңдеулерді |
||||||||||||||||||||||||||||
|
|
|
|
|
ɺ |
|
|
|
= 0 Ω3 |
= const . |
|
|
||||||||||||||||
қолданып көрейік. I1 = I 2 болса, Ω3 |
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
(I3 − I1 ) Ω |
3 |
= ω |
|
|
(12) |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
I1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
тұрақтысын енгіземіз. Сонда (11) теңдеуді қайтадан жазуға болады. |
|
|||||||||||||||||||||||||||
|
|
Ω1 = −ωΩ2 , Ω2 = −ωΩ1 . |
|
(13) |
||||||||||||||||||||||||
|
|
ɺ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ɺ |
|
|
|
|
|
|
|
|
|||
Екінші теңдеуге i -ге көбейтіп, онан соң бірінші теңдеуге қосатын болсақ:
110
