Algebra_10kl_RU

УДК 373: [512 + 517] ББК 22.12я721 + 2.161я721

Н49

Рекомендовано Министерством образования и науки Украины

(письмо № 1/11–3169 от 29 июня 2004 г.)

Переведено по изданию:

Нелін Є. П. Алгебра і початки аналізу: Дворівневий підруч. для 10 кл. загальноосвіт. навч. закладів. —

2 е вид., виправ. і доп. — Х.: Світ дитинства, 2006. — 448 с.

Перевел с украинского Е. П. Нелин

Ре ц е н з е н т ы:

М.И. Бурда, член корреспондент АПН Украины, доктор педагогических наук,

профессор, заместитель директора Института педагогики АПН Украины

В. А. Золотарев, доктор физико математических наук, профессор, заведующий кафедрой высшей математики и информатики Харьковского на ционального университета им. В. Н. Каразина

А. Н. Роганин, учитель математики высшей категории, учитель методист Песо чинского коллегиума Харьковского района Харьковской области

Х у д о ж н и к С. Э. Кулинич

У с л о в н ы е о б о з н а ч е н и я в у ч е б н и к е

главное в учебном материале

X начало решения задачи

Y окончание решения задачи

( начало обоснования утверждения

) окончание обоснования утверждения

Нелин Е. П.

Н49 Алгебра и начала анализа: Двухуровневый учеб. для 10 кл. общеоб разоват. учеб. заведений/Пер. с укр. Е. П. Нелина. — Х.: Мир детства, 2006.— 448 с.

ISBN 966 544 379 8 (рус.).

ISBN 966 544 385 2 (укр.).

УДК 373: [512 + 517] ББК 22.12я721 + 2.161я721

Предисловие для учащихся

Вы начинаете изучать новый предмет «Алгебраи начала анализа», который объединяет материал нескольких отраслей математической науки. Как и в курсе алгебры, значительное внимание будет уделено преобразованию выражений, решению уравнений, неравенств и их систем и изучению свойств функций. Наряду с решением знакомых задач, связанных с многочленами, рациональ ными дробями, степенями и корнями, в 10 классе будут рассмотрены новые виды функций: тригонометрические, показательные и логарифмические и со ответствующие уравнения и неравенства.

Принципиально новая часть курса — начала анализа — будет рассматри ваться в 11 классе. Математический анализ (или просто анализ) — отрасль математики, сформированная в XVIII в., которая сыграла значительную роль в развитии природоведения: появился мощный, достаточно универсальный метод исследования функций, которые возникают во время решения разнооб разных прикладных задач.

Несколько замечаний о том, как пользоваться учебником.

Система учебного материала учебника по каждой теме представлена на двух уровнях. Основной материал приведен в параграфах, номера которых обозначены синим цветом. Дополнительный материал (номера параграфов обозначены серым цветом) предназначен для овладения темой на более глубо ком уровне и может осваиваться учеником самостоятельно или под руковод ством учителя при изучении математики в классах универсального или есте ственного профилей, а может использоваться для систематического изуче ния углубленного курса алгебры и начал анализа в классах, школах, лицеях

игимназиях физико математического профиля.

Вначале многих параграфов приводятся справочные таблицы, которые со держат основные определения, свойства и ориентиры по поиску плана решения задач по теме. Для ознакомления с основными идеями решения задач приводят ся примеры, в которых, кроме самого решения, содержится также коммента( рий, который поможет составить план решения аналогичного задания.

С целью закрепления, контроля и самоконтроля усвоения учебного мате риала после каждого параграфа предлагается система вопросов и упражне ний. Ответы на эти вопросы и примеры решения аналогичных упражнений можно найти в тексте параграфа. Система упражнений к основному материа

лу дана на трех уровнях. Задачи среднего уровня обозначены символом «°», более сложные задачи достаточного уровня даны без обозначений, а задачи высокого уровня сложности обозначены символом «*». В учебнике и для мно гих задач углубленного уровня предлагаются специальные ориентиры, по зволяющие освоить методы их решения. Ответы и указания для большин ства упражнений приведены в соответствующем разделе. О происхождении понятий, терминов и символов вы узнаете, прочитав «Сведения из истории». В конце учебника приведен справочный материал.

3

Предисловие для учителя

Предлагаемый учебник направлен на реализацию основных положений кон цепции профильного обучения в старшей школе, на организацию личностно ориентированного обучения математике. Учебник подготовлен в соответствии

сдействующей программой по алгебре и началам анализа для 10–11 классов

сучетом программы по алгебре и началам анализа для 10–12 классов. Отметим основные отличия предложенного учебника от других учебников

по алгебре и началам анализа.

Это двухуровневый учебник, который содержит общий материал для клас сов универсального, естественного и физико математического профилей и до полнительный материал для классов физико математического профиля.

Вкаждом разделе наряду с параграфами, предназначенными для овладения учениками стандартного математического образования на академическом уравне, есть систематический материал, предназначенный для организации индивидуальной работы с учениками, которые интересуются математикой. Предложенный дополнительный материал может использоваться и для орга низации обучения алгебре и началам анализа в классах физико математиче ского профиля или в специализированных школах и классах с углубленным изучением математики.

Основной материал, который должны усвоить ученики, структурирован в форме справочных таблиц в начале параграфа, содержащих систематиза цию теоретического материала и способы деятельности с этим материалом в форме специальных ориентиров по решению задач. В первую очередь уче ники должны усвоить материал, который содержится в таблицах. По этому при объяснении нового материала целесообразно применить работу с учебником по соответствующим таблицам и рисункам. Все необходимые по яснения и обоснования тоже приведены в учебнике, но каждый ученик может выбирать свой собственный уровень ознакомления с этими обоснованиями.

Вкаждом разделе решению упражнений предшествует выделение общих ори ентиров по решению таких задач. Поэтому важной составляющей работы с пред ложенным учебником является обсуждение выбора соответствующих ориен тиров и планов решения задач. Пояснение методов решения ведется по схеме:

При такой подаче учебного материала комментарий, в котором поясняет ся решение, не мешает восприятию основной идеи и плана решения задач определенного типа. Это позволяет ученику, который уже усвоил способ ре шения, с помощью приведенного примера вспомнить, как решать задания, а ученику, которому необходима консультация по решению, — получить та кую детальную консультацию, содержащуюся в комментарии.

4

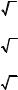
За счет четкого выделения общих ориентиров работы с практическими зада ниями курса удается часть «нестандартных» (с точки зрения традиционных учебников) задач перевести в разряд «стандартных» (например, уравнения, для решения которых приходится применять свойства функций). Это позволяет уменьшить разрыв между уровнем требований государственной аттестации по алгебре и началам анализа и уровнем требований по этому курсу на вступи тельных экзаменах в вузы, а также ознакомить учеников с методами решения задач, которые предлагаются на вступительных экзаменах в вузы.

Заметим, что детальная систематизация по содержательным линиям учеб ного материала и соответствующим способам деятельности по решению за дач курса содержится также в пособии Е. П. Нелина «Алгебра в таблицах. Учебное пособие для учащихся 7–11 классов».— Харьков: Мир детства, 1998– 2005, которое целесообразно использовать в учебном процессе в комплекте с учебником.

Обозначения, встречающиеся в учебнике

5

Раздел 1

Тригонометрические функции

§ПОВТОРЕНИЕ И РАСШИРЕНИЕ 1 СВЕДЕНИЙ О ФУНКЦИИ

1.1.ПОНЯТИЕ ЧИСЛОВОЙ ФУКЦИИ. ПРОСТЕЙШИЕ СВОЙСТВА ЧИСЛОВЫХ ФУНКЦИЙ

Та б л и ц а 1

1.Понятие числовой функции

Числовой функцией с областью оп ределения D называется зависи мость, при которой каждому числу x из множества D (области определе ния) ставится в соответствие един ственное число y.

Записывают это соответствие так: y = f (x).

Обозначения и термины

D (f) — область определения E (f) — область значений

x — аргумент (независимая переменная)

y — функция (зависимая переменная)

f — функция

f (x0)— значение функции f в точке x0

2. График функции

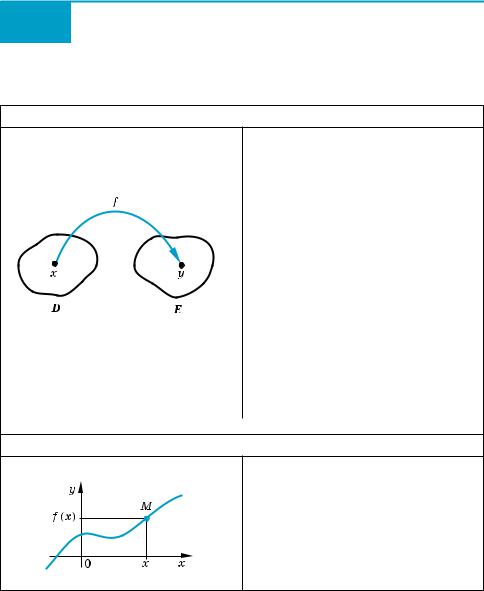
Графиком функции f называется множество всех точек координат ной плоскости с координатами (x; f (x)), где первая координата x «пробегает» всю область определе ния функции, а вторая координа та равна соответствующему значе нию функции f в точке x.

6

§1. Повторение и расширение сведений о функции

Пр о д о л ж. т а б л. 1

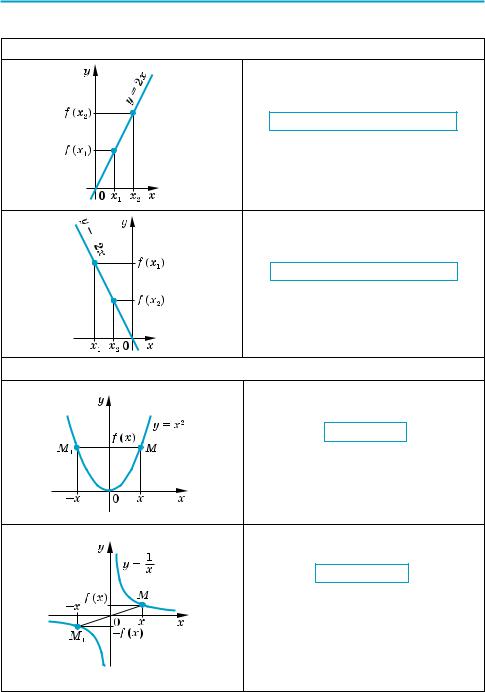
3.Возрастающие и убывающие функции

Функция f (x) возрастающая:

если х2 > x1, то f (x2) > f (x1)

(при увеличении аргумента соответ ствующие точки графика поднима ются).

Функция f (x) убывающая:

если x2 > x1, то f (x2) < f (x1)

(при увеличении аргумента соот ветствующие точки графика опус каются).

4. Четные и нечетные функции

Функция f (x) четная:

f (–x) = f (x)

для всех x из области определения.

График четной функции симметри чен относительно оси Oy.

Функция f (x) нечетная:

f (–x) = –f (x)

для всех x из области определения.

График нечетной функции сим метричен относительно начала координат (точки О).

7

РАЗДЕЛ 1. Тригонометрические функции

Объяснение и обоснование

1. Понятие функции. С понятием функции вы ознакомились в курсе алгеб ры. Напомним, что зависимость переменной y от переменной x называется функцией, если каждому значению x соответствует единственное значение y.

В курсе алгебры и начал анализа мы будем пользоваться таким определе нием числовой функции.

Числовой функцией с областью определения D называется зависимость, при которой каждому числу x из множества D ставится в соответствие единственное число y.

Функции обозначают латинскими (иногда греческими) буквами. Рассмот рим произвольную функцию f. Число y, соответствующее числу x (на рисун ке 1 это показано стрелкой), называют значением функции f в точке x и обо значают f (x).

Область определения функции f — это множество тех значений, которые может принимать аргумент x. Она обозначается D (f).

Область значений функции f — это множество, состоящее из всех чисел f (x), где x принадлежит области определения. Ее обозначают E (f).

Чаще всего функцию задают с помощью какой либо формулы. Если нет дополнительных ограничений, то областью определения функции, заданной формулой, считается множество всех значений переменной, при которых эта формула имеет смысл.

Например, если функция задана формулой y = x + 1 , то ее область опре деления: x 0, то есть D (y) = [0; + ), а область значений: y 1, то есть E (y) = [1; + ).

Иногда функция может задаваться разными формулами на разных множе

x при x 0, ствах значений аргумента. Например, y = x = −x при x < 0.

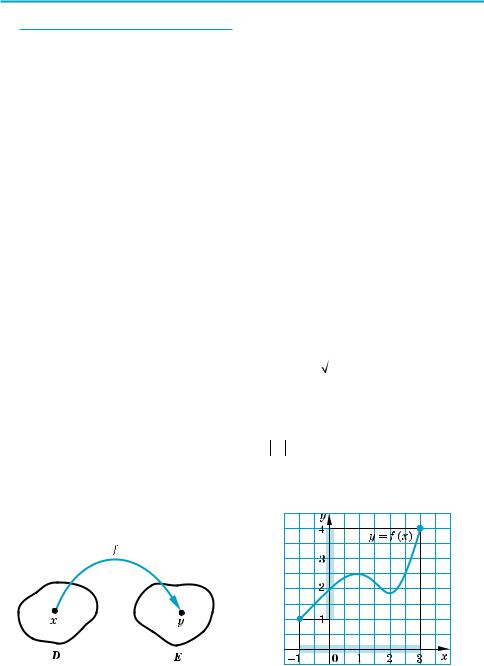
Функция может задаваться не только с помощью формулы, а и с помощью таблицы, графика или словесного описания. Например, на рисунке 2 графи

8

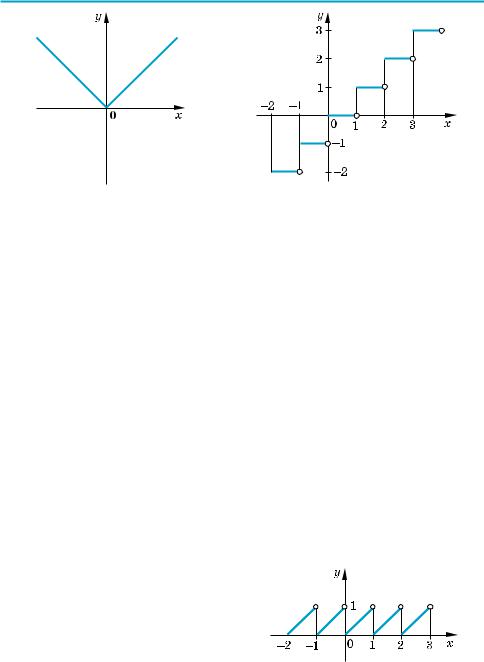
§ 1. Повторение и расширение сведений о функции

чески задана функция y = f (x) с областью определения D (f) = [–1; 3] и множе ством значений E (f) = [1; 4].

2.График функции. Напомним, что

графиком функции y = f (x) называется множество всех точек коорди натной плоскости с координатами (x; f (x)), где первая координата x «про бегает» всю область определения функции, а вторая координата — это соответствующее значение функции f в точке x.

На рисунках к пункту 4 таблицы 1 приведены графики функций y = x2

и y = 1 , а на рисунке 3 — график функции y = | x |. x

Приведем также график функции y = [x], где [x] — обозначение целой части числа x, то есть наибольшего целого числа, не превосходящего x (рис. 4). Об ласть определения этой функции D (y) = R — множество всех действительных чисел, а область значений E (y) = Z — множество всех целых чисел.

На рисунке 5 приведен график еще одной числовой функции y = {x}, где {x} — обозначение дробной части числа x (по определению {x} = x – [x]).

3. Возрастающие и убывающие функции. Важными характеристиками функ ций являются их возрастание и убывание.

Функция f (x) называется возрастающей на множестве Р, если большему

значению аргумента из этого множества соответствует большее значение функции.

9

РАЗДЕЛ 1. Тригонометрические функции

f (x2) > f (x1). У возрастающей функции при увеличении аргумента соответ ствующие точки графика поднимаются (рис. 6).

На рисунке 7 приведен график еще одной возрастающей функции у = х3. Действительно, при x2 > x1 имеем x23 > x13, то есть f (x2) > f (x1).

Функция f(x) называется убывающей на множестве Р, если большему значению аргумента из этого множества соответствует меньшее значе ние функции.

То есть для любых двух значений x1 и x2 из множества Р, если x2 > x1, то

f (x2) < f (x1).

Например, функция f (x) = –2x убывающая (на всей области определе ния — на множестве R), поскольку при x2 > x1 имеем –2x2 < –2x1, то есть f (x2) < f (x1). У убывающей функции при увеличении аргумента соответству ющие точки графика опускаются (рис. 8).

Рассматривая график функции y = x2 (рис. 9), видим, что на всей области определения эта функция не является ни возрастающей, ни убывающей. Од нако можно выделить промежутки области определения, где эта функция возрастает и где убывает. Так, на промежутке [0; + ) функция y = x2 возрас тает, а на промежутке (– ; 0] — убывает.

Отметим, что для возрастающих и убывающих функций выполняются свойства, обратные утверждениям, содержащимся в определениях.

Если функция возрастает, то большему значению функции соот ветствует большее значение аргумента.

Если функция убывает, то большему значению функции соответ ствует меньшее значение аргумента.

(Обоснуем первое из этих свойств методом от противного. Пусть функция

f (x) возрастает и f (x2) > f (x1). Допустим, что аргумент x2 не больше аргу мента x1, то есть x2 m x1. Из этого предположения получаем:

если x2 x1 и f (x) возрастает, то f (x2) f (x1), что противоречит условию f (x2) > f (x1). Таким образом, наше предположение неверно, и если f (x2) > f (x1), то x2 > x1, что и требовалось доказать.

Аналогично обосновывается и второе свойство. )

10

§ 1. Повторение и расширение сведений о функции

Например, если x3 > 8, то есть x3 > 23, то, учитывая возрастание функции f (x) = x3, получаем x > 2.

4. Четные и нечетные функции. Рассмотрим функции, области определения которых симметричны относительно начала координат, то есть содержат вме сте с каждым числом x и число (–x). Для таких функций вводятся понятия четности и нечетности.

Функция f называется четной, если для любого x из ее области определе ния f (–x) = f (x).

Например, функция y = x2 (то есть функция f (x) = x2) — четная, поскольку f (–x) = (–x)2 = x2 = f (x).

(Если функция f (x) четная, то ее графику вместе с каждой точкой M с ко

ординатами (x; y) = (x; f (x)) принадлежит также и точка M1 с координата ми (–x; y) = (–x; f (–x)) = (–x; f (x)). Точки M и M1 расположены симмет рично относительно оси Oy (рис. 10), поэтому и весь график четной функ ции расположен симметрично относительно оси Oy. )

Например, график четной функции y = x2 (рис. 9) симметричен относи тельно оси Oy.

Функция f называется нечетной, если для любого x из ее области опреде ления f (–x) = –f (x).

Например, функция y = x1 (то есть функция f(x) = x1 ) — нечетная, поскольку

f(−x) = 1 = − 1 = −f(x) .

−x x

(Если функция f (x) нечетная, то ее графику вместе с каждой точкой M с

координатами (x; y) = (x; f (x)) принадлежит также и точка M1 с координа тами (–x; y) = (–x; f (–x)) = (–x; –f (x)). Точки M и M1 расположены сим метрично относительно начала координат (рис. 11), поэтому и весь гра

фик нечетной функции расположен симметрично относительно начала координат. )

Например, график нечетной функции y = 1 (см. пункт 4 табл. 1) симмет

11